1. При теплообмене путем теплопроводности тепловой поток проходит от изотермической поверхности с более высокой температурой Q 1 к изотермической поверхности с более низкой температурой Q 2. В одномерном тепловом поле через площадку площадью Q, перпендикулярную текстовому потоку, проходит поток мощностью
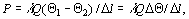(4.211)
где l – коэффициент теплопроводности; D Q = Q 1 – Q 2 – изменение температуры при переходе с одной изотермической поверхности на другую, расположенную на расстоянии D l.
Предел lim(D Q /D l) при D l® 0 называется градиентом температуры в данной точке тела. Коэффициент теплопроводности l очень мал у газов, несколько больше у жидких тел и еще больше у твердых. Особенно велик он у металлов.
2. Конвекция имеет место на границе раздела твердого тела с жидкостью или газом или жидкости с газом. Она бывает естественной и вынужденной (принудительной). Естественная конвекция происходит при тепловом расширении жидкости и газа вследствие изменения их плотности. Более теплые частицы вытесняются вверх более холодными, имеющими большую плотность. Смена теплых частиц холодными возле поверхности тела приводит к ее теплоотдаче. Вынужденная конвекция происходит вследствие перемешивания жидкости или газа искусственным путем. Она всегда сопровождается естественной. Однако в этом случае роль естественной конвекции может быть невелика. Мощность теплового конвективного потока, проходящая через границу раздела двух сред,
(4.212)
где Qp – площадь поверхности раздела двух сред, имеющих температуры Q 1 и Q 2, a – коэффициент теплообмена.
Значение a зависит от многих факторов: температуры, теплоемкости сред, их плотности, вязкости и других параметров. Его значение сильно увеличивается при увеличении скорости обтекания поверхности раздела.
3. Все тела излучают энергию, причем зависимость мощности излучения от абсолютной температуры Т определяется соотношением
(4.213)
где С – коэффициент излучения тела, зависящий от состояний его поверхности.
Одновременно с излучением тело поглощает излучение других тел. Мощность теплообмена излучением между двумя телами, имеющими абсолютные температуры Т 1и Т 2равна
(4.214)
где С 12 – некоторый эффективный коэффициент излучения, зависящий от коэффициентов излучения одного и другого тела.
Рассмотрим более подробно теплообменный процесс термометра. Термометр 1 (рис. 4.79, а) монтируется в стенке 2 объекта, температуру среды Q 1 внуки которого требуется измерить. Конец термометра, находящийся в объекте, омывается горячим потоком вещества, и в термометр конвективным путем вводится тепловой поток q. Он проходит по телу термометра, нагревает стенку в месте его монтажа, проходит далее по холодному концу термометра и рассеивается в окружающей среде. Распределение температур вдоль термометра схематически показано на рис. 4.79, б. Для того чтобы температура чувствительного конца термометра Q 2 была близка к температуре Q 1, нужно увеличить тепловой поток, нагревающий термометр. Мощность этого потока определяется выражением (4.212) и зависит от коэффициента теплопередачи a .. Значение a мало при естественной конвекции и возрастает при принудительной конвекции с увеличением скорости потока возле термометра. При измерении температуры жидкостей или газов, проходящих по трубам, для увеличения а чувствительную часть термометра нужно помещать в таком месте, где поток турбулентен и его скорость наибольшая (рис. 4.80). Поток завихрятся на изгибах трубопровода, в местах сужения и у других местных сопротивлений. На прямолинейных участках скорость потока максимальна в середине сечения трубы. Для увеличения точности измерения температуры горячих, например дымовых, газов, когда скорость газа в основной трубе недостаточна, используют так называемую отсасывающую термопару. Она представляет собой трубку малого диаметра, врезанную в основной трубопровод; в трубку с некоторым зазором вставлена термопара. Газ прокачивается через трубку мимо термопары. Скорость отсоса газа должна быть такова, чтобы коэффициент теплопередачи был близок к максимальному.
Мощность проходящего через термометр теплового потока возрастает с увеличением площади теплообмена. Площадь можно увеличить увеличением глубины погружения термометра.
Температура вдоль термометра меняется от температуры Q 2 (рис. 4.79), близкой к измеряемой температуре, до температурыQ 4, близкой к внешней температуре Q 5. Вдоль термометра имеется градиент температуры и существует тепловой поток, обусловленный теплопроводностью. Если измерительный конец термометра получает тепло от окружающей его среды только путем конвекции, то дружине участки термометра, находящиеся внутри объекта, получают тепло также и путем теплопроводности от более нагретых участков (рис. 4.79, а). Вследствие этого при удалении от стенки объекта 2 градиент температур D Q /D l в термометре уменьшается, также уменьшается и тепловой поток, передаваемый путем теплопроводности. В пределе при очень большой длине термометра l внутри объекта градиент температуры D Q /D l на чувствительном конце стремится к нулю, к нулю стремится и тепловой поток, передаваемый от него путем теплопроводности. Если нет других потерь тепла, то температура Q 2 будет равна температуре окружающей среды Q 1.
Длину термометра не всегда можно увеличить по конструктивно-монтажным соображениям. В этом случае для уменьшения теплового потока, исходящего от измерительного конца, можно рекомендовать теплоизоляцию его противоположного конца и места прохода через стенку объекта. Это повышает температуру всего термометра и уменьшает градиент температуры возле его измерительного конца.
Измерительный конец термометра участвует в теплообмене излучением со стенками объекта и другими элементами его конструкции.
Эти элементы могут иметь температуру, отличную от измеряемой, что вызывает потери тепла измерительным концом и увеличивает погрешность измерения. Теплообмен излучением вызывает наибольшую погрешность при измерении высоких температур (более 400 – 500° С), поскольку мощность лучистого теплового потока пропорциональна Т 4. Для уменьшения излучения термометра его внешняя поверхность делается блестящей. Это уменьшает коэффициент излучения C и эффективный коэффициент излучения C12 в формулах (4.213) и (4.214) и уменьшает поток излучения. Другим путем его уменьшения является увеличение температуры Т 2, входящей в формулу (4.214). Это достигается либо путем теплоизоляции стенок объекта, например трубы, по которой проходит горячий газ (рис. 4.80), либо установкой термометра или его измерительного конца 1 в экран 2 с полированными поверхностями (рис. 4.81). Экран имеет температуру, близкую к температуре среды, и мощность теплового излучения, теряемого термометром становится пренебрежимо малой.
Измерение нестационарных температур. Чувствительный элемент термометра обычно находится внутри чехла, защищающего его от различных механических и химических воздействий, как схематически показано на рис. 4.82. Если при постоянной окружающей температуре Q потери тепла пренебрежимо малы, то температура всех элементов датчика (чехла 1 и чувствительного элемента 2) одинакова Q 1 = Q 2. Если же окружающая температура изменяется, то вначале изменяется температура чехла, а затем с некоторым отставанием температура чувствительного элемента. Это обусловливает инерционность датчика.
При рассмотрении динамических свойств датчика температуры полагаем, что присутствие термометра не изменяет температуру окружающей среды и что выравнивание температур в чувствительном элементе и защитном чехле происходит значительно быстрее, чем их нагревание, т. е. в данном поперечном сечении чувствительного элемента и соответственно защитного чехла все точки имеют одинаковую температуру. Это допущение обычно справедливо при измерении температуры промышленными термометрами.
Составим дифференциальное уравнение изменения температуры датчика по схеме, представленной на рис. 432. При увеличении температуры среды Q термометр нагревается. Согласно закону Ньютона количество тепла, прошедшее через границу среда – защитный чехол за время dt, определяется выражением
(4.215)
где а 1 – коэффициент теплопередачи от среды к чехлу; S – площадь поверхности чехла; Q 1 – температура чехла.
Тепло dQ расходуется на нагрев чехла:
(4.216)
где С 1 – теплоемкость чехла, и на нагрев чувствительного элемента:
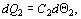(4.217)
где С 2 – теплоемкость чувствительного элемента.
Согласно закону сохранения энергии
(4.218)
Подставив (4.215), (4.216) и (4.217) в (4.218), получим
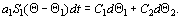(4.219)
Для того чтобы исключить из этого выражения Q 1, воспользуемся уравнением теплового баланса чувствительного элемента
(4.220)
где S2 – поверхность чувствительного элемента; а – коэффициент теплопередачи от чехла к чувствительному элементу.
Продифференцировав это выражение и подставив полученное значение dQ 1/dt в (4.219), получим
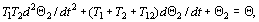(4.221)
где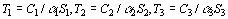 
– постоянные времени чехла, чувствительного элемента и смешанная постоянная времени.
Изменение температуры чувствительного элемента датчика, имеющего один защитный чехол, описывается дифференциальным уравнением второго порядка. Оно имеет апериодическое решение. При скачкообразном изменении измеряемой температуры от Q? до Q?? температура чувствительного элемента Q 2 изменяется в соответствии с уравнением
(4.222)
где А 1 и А 2 – постоянные интегрирования; р 1и р 2 – корни характеристического уравнения
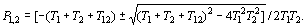(4.223)
График изменения температуры Q 2 показана на рис. 4.83.
Датчик температуры с одним чехлом является инерционным звеном второго порядка. Из теории автоматического регулирования известно, что такое звено может быть представлено в виде двух последовательно включенных инерционных звеньев первого порядка. Этим звеньям соответствуют дифференциальные уравнения первого порядка. Одно уравнение описывает процесс нагрева чехла, другое – процесс нагрева чувствительного элемента. Переходный процесс термометра зависит как от свойств и характеристик преобразователя (Т 2), так и от свойств и характеристик среды, температуры которой измеряется (Т 1 и T12).
При аттестации динамических свойств датчика его испытания ведут в таких условиях, чтобы параметры среды вливали минимально. Для этого термометр опускается в сосуд с кипящей, непрерывно перевешиваемой водой. Благодаря интенсивному перемешиванию сильно возрастает коэффициент теплопередачи а 1, и уменьшаются постоянные времени Т 1 и T12. В пределе они стремятся кнулю, и уравнение (4.221) вырождается в дифференциальное уравнение первого порядка
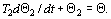(4.224)
При скачкообразном изменении измеряемой температуры на D Q = Q?? – Q? градусов решение описывается выражением
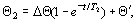(4.225)
где Q? – начальная температура термометра.
В условиях реального динамического испытания начальный участок графика переходного процесса отличается от экспоненты. Это отличие обусловлено тем, что Т 1 ? 0, Т 12 ? 0, а также тем, что в различных точках сечения датчика и чехла температура устанавливается не одновременно.
Для определения интервала времени, в котором температура изменяется экспоненциально, строится график функции lnD Q = f(t) (рис. 4.84). Линейный участок кривой соответствует экспоненциальному изменению температуры. Величина
(4.226)
где t1 и t2 – время начала и конца линейной части графика; D Q 1 и D Q 2 – соответствующие изменения температуры, называется постоянной тепловой инерцией датчика температуры. Она близка к постоянной времени Т 2 и является паспортной величиной.
