6.1. Вводные замечания
При обработке результатов измерений используют математический аппарат теории вероятности и математической статистики [46, 49, 50, 51]. Однако теоретические модели далеки от реальных процессов, поэтому при обработке результатов измерений производят оценку истинных значений измеряемых физических величин. В связи с этим введены специальные обозначения, чтобы отличить теоретические значения от значений, полученных экспериментальным путем, (см. табл. 6).
Таблица 6
Обозначения теоретических и экспериментальных значений результатов измерений
| Теоретические значения | Экспериментальные значения | ||
| обоз-начение | название | обозна-чение | название |
| Математическое ожидание |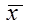 
| Среднее арифметическое |
| Оценка математического ожидания | ||
| СКО в ряду наблюдений | 
| Оценка СКО в ряду наблюдений |
| СКО математического ожидания | 
| Оценка СКО математического ожидания |
| Оценка СКО среднего арифметического |
Средняя квадратическая погрешность результатов единичных измерений в ряду измерений – оценка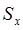 
рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около среднего их значения, вычисляемая по формуле
,
где 
- результат i -го единичного измерения; 
- среднее арифметическое значение измеряемой величины из n единичных результатов.
Ранее эта числовая характеристика называлась СКО результата наблюдения. Ее теоретическое значение равно
.
Примечание: в теоретическом значении в скобках стоит математическое ожидание и деление при этом происходит на количество измерений n в отличие от экспериментального значения, где в скобках стоит среднее арифметическое и деление происходит на (n -1).
Средняя квадратическая погрешность результата измерений среднего арифметического – оценка 
случайной погрешности среднего арифметического значения результата измерений одной и той же величины в данном ряду измерений, вычисляемая по формуле
,
где 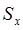- средняя квадратическая погрешность результатов единичных измерений, полученная из ряда равноточных измерений; n – число единичных измерений в ряду.
Ранее эта числовая характеристика называлась СКО результата измерений
