В результате измерения получают значение измеряемой величины в виде числа в принятых единицах величины. Погрешность измерения тоже удобно выражать в виде числа. Однако погрешность измерения является случайной величиной, исчерпывающим описанием которой может быть только закон распределения. Из теории вероятностей известно, что закон распределения можно охарактеризовать числовыми характеристиками (неслучайными числами), которые и используются для количественной оценки погрешности.
Примечание: Ранее применялись различные обозначения, которые до сих пор встречаются в технической литературе по метрологии, поэтому они здесь и приводятся. В настоящее время существует ГОСТ Р 50779.10-2000 (ИСО 3534.1-93) «Статистические методы. Вероятность и основы статистики. Термины и определения».
Систематическая погрешность Dс - разность между математическим ожиданием 
результатов наблюдения измеряемой величины x и истинным значением 
:
,
где 
- математическое ожидание (различные обозначения одной и той же величины, встречающиеся в технической литературе по метрологии);
- функция распределения случайной величины x.
Случайная погрешность 
- разность между результатом единичного наблюдения и математическим ожиданием результата измерения:
Математическое ожидание погрешности 
равно математическому ожиданию систематической погрешности (составляющей), так как математическое ожидание случайной погрешности всегда равно нулю:
.
Промахом, или грубой погрешностью, называется погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Поскольку грубые погрешности относятся к случайным, для их выявления и исключения применяют методы теории вероятности и математической статистики.
Под интегральной функцией распределения результатов наблюдений понимается зависимость вероятности того, что результат наблюдения в i -м опыте окажется меньшим некоторого текущего значения х i, от самой величины х:
.
Латинская буква Р является здесь символом вероятности события. Интегральная функция распределения результатов наблюдений является неубывающей функцией аргумента и определена в диапазоне
.
Обычно график интегральной функции распределения результатов наблюдений представляет собой непрерывную неубывающую кривую, начинающуюся от нуля на отрицательной бесконечности и асимптотически приближающуюся к единице при увеличении аргумента до плюс бесконечности.
Случайную погрешность Δ тоже следует рассматривать как случайную величину, принимающую в разных опытах различные значения Δi. Ее интегральную функцию распределения получаем переносом начала координат в точку х = Q, где Q – истинное значение измеряемой величины:
.
В некоторых случаях более удобным является описание свойств результатов наблюдений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей и обозначаемой через fх(х) или обозначается через f Δ(Δ). Иногда используется обозначение pх(х) или соответственно через p Δ(Δ). Дифференциальная функция распределения является функцией, производной от интегральной по своему аргументу:
.
График дифференциальной функции распределения, который называют кривой распределения, чаще всего имеет колоколообразную форму и обладает максимумом при х = Q или соответственно Δ = 0.
От дифференциальной функции распределения легко перейти к интегральной путем интегрирования первой
. (3.1)
Поскольку 
, то справедливо следующее равенство:
.
Для интегральной функции распределения справедливо следующее утверждение: вероятность попадания результата наблюдений или случайной погрешности в заданный интервал равна разности значений функции распределения на границах этого интервала т. е..
Для погрешностей:
Функция распределения является самым универсальным способом описания поведения случайных погрешностей. Однако для определения функций распределения необходимо проведение весьма кропотливых научных исследований и обширных вычислительных работ. Поэтому к такому способу описания случайных погрешностей прибегают в исключительных случаях, а используют специальные величины.
Начальным моментом r -го порядка результатов наблюдений называется интеграл вида
,
представляющий собой математическое ожидание степени 
. Откуда следует, что первый начальный момент совпадает с математическим ожиданием результатов наблюдений: 
.
Центральным моментом r -го порядка результатов наблюдений называется интеграл вида
,
представляющий собой математическое ожидание величины 
,т. е. r -й степени случайной погрешности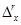 
.
Можно показать, что первый центральный момент результатов наблюдений тождественно равен нулю.
.
Начальные и центральные моменты случайных погрешностей совпадают между собой и с центральными моментами результатов наблюдений: 
, поскольку математическое ожидание случайных погрешностей равно нулю.
Вычислим второй центральный момент, называемый дисперсией результатов наблюдений и обозначаемый через 
:
,
где 
— символ математического ожидания погрешности;
— символ дисперсии.
Математическое ожидание погрешности измерений 
- есть неслучайная величина,1 относительно которой рассеиваются другие значения погрешностей, при повторных измерениях
. (3.2)
Математическое ожидание погрешности характеризует систематическую составляющую погрешности измерения 
. Как числовая характеристика погрешности показывает на смещенность результатов измерения относительно истинного значения измеряемой величины.
Дисперсия погрешности 
характеризует степень рассеивания (разброса) отдельных значений погрешности относительно математического ожидания. Так как рассеивание происходит за счет случайной составляющей погрешности то 
. Чем меньше дисперсия, тем меньше разброс, тем точнее выполнены измерения. Следовательно, дисперсия может служить характеристикой точности проведенных измерений. Однако размерность дисперсии выражается в единицах величины в квадрате. Поэтому в качестве числовой характеристики точности измерений используют стандартное отклонение (среднеквадратическое отклонение СКО, среднеквадратическая погрешность, СКП)
с положительным знаком и выражаемое в единицах погрешности (и, естественно, совпадающей с единицей измеряемой физической величины).
В настоящее время вводятся также новые понятия, параллельные прежней терминологии, например, следующие:
Правильность – степень близости результата измерений к истинному (действительному) значению измеряемой величины.
Показателем правильности является отсутствие или малая величина систематической погрешности, т.е. близость математического ожидания (среднего значения) к истинной величине.
Прецизионность - степень близости друг к другу независимых результатов измерений, полученных в конкретных регламентированных условиях.
Показателем прецизионности является отсутствие или малая величина случайных погрешностей (или их обобщенная характеристика – стандартное отклонение). Прецизионность в бытовом понимании – кучность.
Обычно при проведении измерений стремятся получить результат измерения с погрешностью, не превышающей допускаемое значение. Знание только стандартного отклонения не позволяет найти максимальную погрешность, которая может встретиться при измерениях, что свидетельствует об ограниченных возможностях такой числовой характеристики погрешности, как 
. Более того, при разных условиях измерений, когда законы распределения погрешностей могут отличаться друг от друга, погрешность с меньшей дисперсией может принимать большие значения.
Максимальные значения погрешности зависят не только от 
, но и от вида закона распределения. Когда распределение погрешности теоретически неограниченно, например, при нормальном законе распределения, погрешность может быть любой по значению. В этом случае можно лишь говорить об интервале, за границы которого погрешность не выйдет с некоторой вероятностью. Этот интервал называют доверительным интервалом, характеризующую его вероятность — доверительной вероятностью, а границы этого интервала — доверительными значениями погрешности.
В практике измерений применяют различные значения доверительной вероятности, например: 0,90; 0,95; 0,98; 0,99; 0,9973, 0,999 и даже выше, когда связано с безопасностью и здоровьем людей. Доверительный интервал и доверительную вероятность выбирают в зависимости от конкретных условий измерений.
В настоящее время в нормативных документах, если нет веских оснований, рекомендовано принимать значения доверительной вероятности равным 0,95 для обычной практики измерений и 0,99 для точных измерений или в случае, когда измерения нельзя повторить.
Доверительный интервал является одной из основных характеристик точности измерений. Одна из форм представления результата измерения устанавливается в следующем виде:
х; Dх от 
до 
*; Р,
где х — результат измерения в единицах измеряемой величины; 
, и — соответственно погрешность измерения с нижней и верхней ее границами в тех же единицах ( и должны быть указаны со своими знаками. В общем случае может быть не равна .); Р — вероятность, с которой погрешность измерения находится в этих границах.
Если границы погрешности симметричны, т. е. 
, то результат измерения может быть записан так:
Допускаются и другие формы представления результата измерения, отличающиеся от приведенной формы тем, что в них указывают раздельно характеристики систематической и случайной составляющих погрешности измерения. При этом для систематической погрешности указывают ее вероятностные характеристики.
Ранее уже отмечалось, что иногда систематическую погрешность приходится оценивать с вероятностных позиций. В этом случае основными характеристиками систематической погрешности являются 
, 
и ее доверительный интервал.
Выделение систематической и случайной составляющих погрешности целесообразно, если результат измерения будет использован при дальнейшей обработке данных, например при определении результата косвенных измерений и оценке его точности, при суммировании погрешностей и т. п.
Любая из форм представления результата измерения должна содержать необходимые данные, на основании которых может быть определен доверительный интервал для погрешности результата измерения. В общем случае доверительный интервал может быть установлен, если известен вид закона распределения погрешности и основные числовые характеристики этого закона.
На рис. 2 графически изображены погрешности измерений.
Рис. 2. Погрешности измерений
3.5. НЕРАВЕНСТВО ЧЕБЫШЕВА
Оценим вероятность того, что при однократном наблюдении случайная погрешность по абсолютной величине не превзойдет некоторой наперед заданной величины e, т. е. вероятность 
. Для этого воспользуемся выражением для дисперсии случайной погрешности и запишем в следующем виде:
.
Исключим второе слагаемое из правой части, что равносильно сужению пределов интегрирования. Правая часть равенства при этом возрасти не может, поэтому имеет место следующее неравенство:
.
При замене под знаком интеграла Δ 2 на меньшую величину e 2 неравенство может только усилиться:
Интегралы в квадратных скобках представляют собой, согласно формуле, вероятности того, что случайная погрешность примет значения, лежащие в интервалах, определяемых пределами интегрирования:
.
Отсюда получаем окончательно
. (3.3)
Этот результат известен как неравенство Чебышева или неравенство Бьеноме-Чебышева.
Полагая 
, найдем вероятность того, что результат однократного наблюдения отличается от истинного значения на величину, большую утроенного среднего квадратического отклонения, т. е. вероятность того, что случайная погрешность окажется большей 
.
Вероятность того, что погрешность измерения не превысит составит
Неравенство Чебышева дает только нижнюю границу для вероятности ,меньше которой она не может быть ни при каком распределении. Обычно 
значительно больше 89%. Так, например, в случае нормального распределения погрешностей эта вероятность составляет 99,73 %.
3.6. ОЦЕНКА ДИСПЕРСИИ
Ввиду широкого использования в технических приложениях приведем выражение для вычисления оценки дисперсии, которую можно представить в виде
(3.4)
Докажем это утверждение.
Предварительно напомним, что в математической статистики, для оценок истинного значения, найденного по экспериментальным наблюдениям, предъявляются требования состоятельности, несмещенности и эффективности.
Оценка называется состоятельной, если при увеличении числа наблюдений она стремится к истинному значению оцениваемой величины.
Оценка называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемой величины.
Оценка называется эффективной, когда ее дисперсия, найденная из нескольких оценок, является наименьшей.
Не трудно убедиться, что среднеарифметическая величина 
, которую мы используем вместо математического ожидания 
, удовлетворяет всем этим требованиям.
Рассмотрим выражения для дисперсии.
По определению, дисперсия случайной величины x имеет вид
,
где 
- вероятность появления события 
, а дисперсия случайной величины (среднеарифметического) равна
.
Приведенные выражения имеют недостаток – в них входит неизвестная величина математическое ожидание , которая для нас остается неизвестной. Поэтому нам хотелось бы заменить эту неизвестную величину известной величиной – среднеарифметической.
Однако при этом сразу возникает вопрос - насколько данная оценка будет удовлетворять требованиям состоятельности, несмещенности и эффективности и каким будет формула для вычисления оценки дисперсии?
Исследуем оценку дисперсии 
. Для этого запишем
Проанализируем слагаемые
и запишем результат
Таким образом, произведя несложные преобразования, окончательно получим:
.
Для оценки дисперсии введено специальное обозначение 
(мы использовали обозначение только для обозримости вывода). В новых общепринятых обозначениях формулы имеют вид
(3.5)
и
. (3.6)
Легко убедиться, что полученная оценка дисперсии удовлетворяет требованиям состоятельности, несмещенности и эффективности. Читатель может в этом убедиться самостоятельно, проведя проверку по определению.
Полным описанием случайной величины, а следовательно и погрешности, является ее закон распределения, которым определяется характер проявления различных результатов отдельных измерений.
