Всякая зависимость (уравнение), описывающая некоторое физическое явление и связывающая между собой 
физическую величину, среди которых 
-обладают независимыми размерностями, может быть преобразовано к зависимости (уравнению), связывающей 
безразмерных комплексов, составленных из величин с зависимой размерностью.
Доказательство.
Пусть имеем некоторую (размерную или безразмерную) величину, которая является функцией независимых между собой размерных величин 
.
(2.3)
Пусть теперь среди размерных величин первые величины 
имеют независимые размерности. Примем величин с независимыми размерностями за основные величины и введём для их размерностей обозначения 
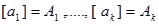
Размерности остальных величин будут иметь вид
Изменим теперь единицы измерения величин 
соответственно в 
раз.
В новой системе единиц соотношение (2.3) примет вид
Это равенство показывает, что функция f обладает свойством однородности относительно единиц измерения величин .
Выберем числа 
для сокращения количества независимых переменных.
Тогда значения первых аргументов будут равны 1, а численные значения параметров 
определятся формулами:
, 
,…, 
,
Числа 
(прописная греческая буква «пи») имеют нулевую размерность и не зависят от выбора системы единиц измерения. Поэтому в любой системе единиц измерения соотношение (1) можно представить в виде
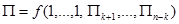(2.4)
где и все аргументы функции 
безразмерные.
ПИ-теорема находит применение при планировании эксперимента и представлении экспериментальных данных.
Теория размерностей подводит теоретическое обоснование системам единиц физических величин.
