Систематической называют погрешность, которая при повторных измерениях одной и той же величины остается постоянной, или изменяется закономерно.
Систематические погрешности обусловлены как несовершенством метода измерений и влиянием средства измерений на измеряемый объект, так и отклонением реальной передаточной характеристики применяемого средства измерений от номинальной характеристики.
Постоянные систематические погрешности средств измерений могут быть выявлены и численно определены в результате сличения их показаний с показаниями эталонных средств измерений. Такие систематические погрешности могут быть уменьшены регулировкой приборов или введением соответствующих поправок. Следует заметить, что полностью исключить систематические погрешности средств измерений не удается, так как их реальные передаточные характеристики изменяются при изменении условий эксплуатации. Кроме этого всегда имеют место так называемые прогрессирующие погрешности (возрастающие или убывающие), вызванные старением элементов входящих в состав средств измерений. Прогрессирующие погрешности могут быть скорректированы регулировкой или введением поправок лишь на некоторое время.
Таким образом, даже после регулировки или введения поправок, всегда имеет место так называемая неисключенная систематическая погрешность результата измерений.
Случайной погрешностью называют погрешность, которая при повторных измерениях одной и той же величины принимает различные значения.
Случайные погрешности обусловлены хаотичным характером изменений физических величин (помех), влияющих на передаточную характеристику средства измерений, суммированием помех с измеряемой величиной, а также наличием собственных шумов средства измерений. При создании средств измерений предусматриваются специальные меры защиты от помех: экранирование входных цепей, использование фильтров, применение стабилизированных источников питающего напряжения и т.д. Это позволяет уменьшить величину случайных погрешностей при проведении измерений. Как правило, при повторных измерениях одной и той же величины результаты измерений либо совпадают, либо отличаются на одну, две единицы младшего разряда. В такой ситуации случайной погрешностью пренебрегают и оценивают только величину неисключенной систематической погрешности.
Наиболее сильно случайные погрешности проявляются при измерении малых значений физических величин. Для повышения точности в таких случаях производятся многократные измерения с последующей статистической обработкой результатов методами теории вероятности и математической статистики.
Промахами называют грубые погрешности, существенно превышающие ожидаемые погрешности при данных условиях проведения измерений.
Промахи большей частью возникают из-за субъективных ошибок экспериментатора или из-за сбоев в работе средства измерений при резких изменениях условий эксплуатации (броски или провалы сетевого напряжения, грозовые разряды и т.п.) Обычно промахи легко выявляются при повторных измерениях и исключаются из рассмотрения.
Оценка погрешностей косвенных измерений.
При косвенных измерениях результат измерений определяется по функциональной зависимости от результатов прямых измерений. Поэтому погрешность косвенных измерений определяется как полный дифференциал этой функции от величин, измеряемых с помощью прямых измерений.

Где: 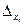 - предельные абсолютные погрешности результатов прямых
- предельные абсолютные погрешности результатов прямых
измерений;
 - предельная абсолютная погрешность результата косвенного
- предельная абсолютная погрешность результата косвенного
измерения;
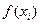 - функциональная связь между искомой измеряемой величиной и
- функциональная связь между искомой измеряемой величиной и
величинами, подвергающимися прямым измерениям.
В частных случаях, когда искомая измеряемая величина будет представляться как функция суммы, разности, произведения, частного или корня от величин, подвергающихся прямым измерениям, погрешность косвенного измерения определяется таблицей 1.
Таблица 1.
| ∆x1 | ∆x2 | x1 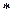 x2 x2
| ∆x1 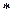 x2 x2
| 
|
| ∆x1 | ∆x2 | x1+x2 | 
| 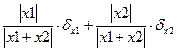
|
| ∆x1 | ∆x2 | x1- x2 | 
| 
|
| ∆x1 | ∆x2 | x1× x2 | 
| 
|
| ∆x1 | ∆x2 | x1: x2 | 
| 
|
| ∆x | xm | 
| 
| |
| ∆x | 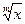
| 
| 
|
Из этой таблицы следует один очень важный практический вывод: необходимо очень осторожно подходить к косвенным измерениям величин, которые являются функциями разности исходных величин, подвергающихся прямым измерениям. При этом могут возникнуть очень большие погрешности даже при очень точных прямых измерениях исходных величин.
I.2.3. Правила округления и записи результата измерений.
Нормирование пределов допустимых погрешностей средств измерений производится указанием значения погрешностей с одной или двумя значащими цифрами. По этой причине при расчете значений погрешностей измерений также должны быть оставлены только первые одна или две значащие цифры. Для округления используются следующие правила:
1. Погрешность результата измерения указывается двумя значащими цифрами, если первая из них более 2, и одной значащей цифрой, если первая из них 3 или более.
2. Показание прибора округляется до того же десятичного разряда, которым заканчивается округленное значение абсолютной погрешности.
3. Округление производится в окончательном ответе, промежуточные вычисления выполняют с одной-двумя избыточными цифрами.
Пример 1
- показание прибора 5,361 В;
- вычисленное значение абсолютной погрешности 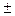 0,284 В;
0,284 В;
- округленное значение абсолютной погрешности 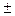 0,26 В;
0,26 В;
- результат измерения (5,36 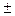 0,26) В.
0,26) В.
Пример 2
- показание прибора 35,67 мА;
- вычисленное значение абсолютной погрешности 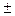 0,541 мА;
0,541 мА;
- округленное значение абсолютной погрешности 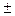 0,5 мА;
0,5 мА;
- результат измерения (35,7 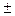 0,5) мА.
0,5) мА.
Пример 3
- вычисленное значение относительной погрешности 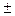 1,268 %;
1,268 %;
- округленное значение относительной погрешности 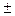 1,3 %.
1,3 %.
Пример 4
- вычисленное значение относительной погрешности 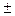 0,367 %;
0,367 %;
- округленное значение относительной погрешности 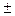 0,4 %.
0,4 %.
I.3. Статистическая обработка результатов измерений
Из-за влияния на средство измерений помех различного происхождения (изменение температуры окружающей среды, электромагнитных полей, вибраций, изменения частоты и амплитуды сетевого напряжения, изменения атмосферного давления, влажности и т.д.), а также из-за наличия собственных шумов элементов, входящих в состав измерительных приборов, результаты повторных измерений одной и той же физической величины (особенно ее малых значений) будут в большей или меньшей степени отличаться друг от друга. В этом случае результат измерений является случайной величиной, которая характеризуется наиболее вероятным значением и разбросом (рассеянием) результатов повторных измерений вблизи наиболее вероятного значения. Если при повторных измерениях одной и той же величины результаты измерений не отличаются друг от друга, то это означает, что разрешающая способность отсчетного устройства не позволяет обнаружить это явление. В этом случае случайная составляющая погрешности измерений является несущественной и ею можно пренебречь. При этом неисключенную систематическую погрешность результата измерений оценивают по величине пределов допускаемых погрешностей применяемых средств измерений. Если же при повторных измерениях одной и той же величины наблюдается разброс показаний, то это означает, что наряду с большей или меньшей неисключенной систематической погрешностью, имеет место и случайная погрешность, принимающая при повторных измерениях различные значения.
Для определения наиболее вероятного значения измеряемой величины при наличии случайных погрешностей и для оценки погрешности, с которой определено это наиболее вероятное значение, применяется статистическая обработка результатов измерений. Статистическая обработка результатов серии измерений при проведении экспериментов позволяет решить следующие задачи.
1. Более точно определить результат измерения путем усреднения отдельных наблюдений.
2. Оценить область неопределенности уточненного результата измерений.
Основной смысл усреднения результатов измерений заключается в том, что найденная усредненная оценка имеет меньшую случайную погрешность, чем отдельные результаты, по которым эта усредненная оценка определяется. Следовательно усреднение не устраняет полностью случайного характера усредненного результата, а лишь уменьшает ширину полосы его неопределенности.
Таким образом, при статистической обработке, прежде всего, определяют наиболее вероятное значение измеряемой величины путем вычисления среднего арифметического всех отсчетов:

где: xi – результат i – го измерения;
n – число проведенных измерений в данной серии измерений.
После этого оценивают отклонение результатов отдельных измерений xi от этой оценки среднего значения  -
-  .
.
Затем находят оценку среднеквадратического отклонения  наблюдений, характеризующую степень рассеяния результатов отдельных наблюдений вблизи
наблюдений, характеризующую степень рассеяния результатов отдельных наблюдений вблизи  , по формуле:
, по формуле:
 .
.
Точность оценки наиболее вероятного значения измеряемой величины  зависит от числа наблюдений
зависит от числа наблюдений  . Нетрудно убедиться в том, что результаты нескольких оценок
. Нетрудно убедиться в том, что результаты нескольких оценок  по одному и тому же числу
по одному и тому же числу  отдельных измерений будут отличаться. Таким образом, сама оценка
отдельных измерений будут отличаться. Таким образом, сама оценка  также является случайной величиной. В связи с этим вычисляется оценка среднеквадратического отклонения результата измерения
также является случайной величиной. В связи с этим вычисляется оценка среднеквадратического отклонения результата измерения  , которую обозначают
, которую обозначают  . Эта оценка характеризует степень разброса значений
. Эта оценка характеризует степень разброса значений  по отношению к истинному значению результата, т.е. характеризует точность результата, полученного усреднением результата многократных измерений. Следовательно, по
по отношению к истинному значению результата, т.е. характеризует точность результата, полученного усреднением результата многократных измерений. Следовательно, по 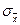 может быть оценена систематическая составляющая результата серии измерений. Для различных
может быть оценена систематическая составляющая результата серии измерений. Для различных  она определяется по формуле:
она определяется по формуле:

Следовательно, точность результата многократных измерений увеличивается с ростом числа последних.
Однако в большинстве практических случаев нам важно определить не просто степень рассеивания значения погрешности при проведении серии измерений (т.е. величину 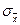 ), а оценить вероятность возникновения погрешности измерения, не превышающую допустимую, т.е. не выходящую за пределы некоторого заданного интервала разброса получаемых погрешностей.
), а оценить вероятность возникновения погрешности измерения, не превышающую допустимую, т.е. не выходящую за пределы некоторого заданного интервала разброса получаемых погрешностей.
Доверительным интервалом 
 называют интервал, который с заданной вероятностью, называемой доверительной вероятностью
называют интервал, который с заданной вероятностью, называемой доверительной вероятностью  накрывает истинное значение измеряемой величины.
накрывает истинное значение измеряемой величины.
При определении доверительных интервалов необходимо, прежде всего, учитывать, что закон распределения погрешностей, получаемых при проведении многократных измерений, при числе измерений в серии меньше 30, описывается не нормальным законом распределения, а так называемым законом распределения Стьюдента. И, в этих случаях, величину доверительного интервала обычно оценивают по формуле:
 ,
,
где  - так называемый коэффициент Стьюдента.
- так называемый коэффициент Стьюдента.
В табл.4.1 приведены значения коэффициентов Стьюдента  в зависимости от заданной доверительной вероятности и числа проведенных наблюдений
в зависимости от заданной доверительной вероятности и числа проведенных наблюдений  . При выполнении измерений обычно задаются доверительной вероятностью 0,95 или 0,99.
. При выполнении измерений обычно задаются доверительной вероятностью 0,95 или 0,99.
Таблица 4.1
Значения коэффициентов Стьюдента  .
.
| n |  
| |||||||
| 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | |
| 1,00 | 1,38 | 1,96 | 3,08 | 6,31 | 12,71 | 31,82 | 63,66 | |
| 0,82 | 1,06 | 1,34 | 1,89 | 2,92 | 4,30 | 6,97 | 9,93 | |
| 0,77 | 0,98 | 1,25 | 1,64 | 2,35 | 3,18 | 4,54 | 5,84 | |
| 0,74 | 0,94 | 1,19 | 1,53 | 2,13 | 2,78 | 3,75 | 4,60 | |
| 0,73 | 0,92 | 1,16 | 1,48 | 2,02 | 2,62 | 3,37 | 4,03 | |
| 0,72 | 0,91 | 1,13 | 1,44 | 1,94 | 2,45 | 3,14 | 3,71 | |
| 0,71 | 0,90 | 1,12 | 1,42 | 1,90 | 2,37 | 3,00 | 3,50 | |
| 0,71 | 0,89 | 1,11 | 1,40 | 1,86 | 2,31 | 2,90 | 3,36 | |
| 0,70 | 0,88 | 1,10 | 1,38 | 1,83 | 2,26 | 2,82 | 3,25 | |
| 0,69 | 0,87 | 1,07 | 1,34 | 1,75 | 2,13 | 2,60 | 2,95 | |
| 0,69 | 0,86 | 1,06 | 1,32 | 1,71 | 2,06 | 2,49 | 2,80 |
Вопросы для самопроверки
1. Чем вызываются погрешности измерений?
2. Перечислите разновидности погрешностей, возникающих в процессе измерений?
3. Какая разница между абсолютной, относительной и приведенной погрешностями измерения и в чем смысл их введения?
4. Чем отличается основная погрешность измерения от дополнительной?
5. Чем отличается методическая погрешность измерения от инструментальной?
6. Чем отличается систематическая погрешность измерения от случайной?
7. Что понимается под аддитивной и мультипликативной оставляющими погрешности?
8. В каких случаях целесообразно использовать статистическую обработку результатов измерений?
9. Какие статистические характеристики обработки наиболее часто используются на практике?
10. Как оценивается неисключенная систематическая погрешность при статистической обработке результатов измерений?
11. Что характеризует величина среднеквадратического отклонения?
12. В чем заключается суть понятий «доверительной вероятности» и «доверительного интервала», используемых при статистической обработке результатов измерений?






