Учитывая, что для объектов СЭС интенсивность отказов в период нормальной эксплуатации практически неизменна, т.е. λ(t) = λ = const, соотношения между основными показателями надежности можно представить с учетом этого условия в более простой и наглядной форме:
, (1.13)
, (1.14)
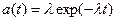. (1.15)
Формулы (1.13) – (1.15) характеризуют экспоненциальный закон надежности, т.е. экспоненциальное распределение времени безотказной работы при отказах с постоянной интенсивностью.
Формула (1.12) для определения средней наработки на отказ для экспоненциального закона принимает вид:
. (1.16)
Для статистической оценки величины Т применяется формула:
, (1.17)
где 
- время безотказной работы i-го элемента (объекта).
Если рассматривается один часто выходящий из строя элемент, то в формуле (1.17) под понимается время безотказной работы на i-м интервале времени, а под N(0) – число временных интервалов.
Для экспоненциального закона надежности средняя наработка элемента до первого отказа равна среднему времени безотказной работы между соседними отказами. Поскольку в период нормальной эксплуатации λ = const, то и Т = const.
Подавляющее большинство объектов СЭС характеризуется очень малыми численными значениями интенсивности отказов и, соответственно, большими значениями средней наработки на отказ и в расчетах возможно использовать упрощенные формулы для расчета показателей надежности:
(1.18)
(1.19)
(1.20)
Упрощенные формулы допустимо применять при λ 
.
Экспоненциальный закон хорошо описывает внезапные отказы, т.е. он справедлив для периода нормальной эксплуатации. Для описания изменений показателей надежности в начальный период эксплуатации и при старении и износе элементов в теории надежности используются другие законы распределения.
