Развитием метода сопоставления является метод совпадения, уменьшающий погрешность отсчета в заданное число k раз без уменьшения в k раз размера меры. Повышение точности достигается путем применения двух многозначных мер (шкал или периодических сигналов) с различными, близкими по значению, размерами однозначных мер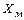 
и 
. При этом осуществляется измерение погрешности квантования 
с помощью совпадения отметок этих шкал. Реализацией метода совпадения является нониусная шкала штангенциркуля (рис. 4.3).
 |
Если шаг квантования условно разбить на k интервалов и выразить погрешность квантования через их целое число 
, то уточненный результат измерения будет равен
, (4.15)
где n – целое число делений основной шкалы.
Если мы хотим, чтобы число m непосредственно отсчитывалось по дополнительной шкале, т.е. было равно числу отметок дополнительной шкалы от нулевой до совпадающей с (n + m)-й отметкой основной шкалы, то должно выполняться условие
,
откуда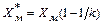 
. (4.16)
Выразив отсюда 
можно записать уравнение измерения (4.15) в виде
. (4.17)
