Из определения силы тока как физической величины видно, что единица силы тока равна количеству электричества, проходящего через поперечное сечение проводника в единицу времени. Поэтому естественно было бы принять за основную электрическую единицу некоторый заряд, например равный заряду электрона или определенного числа электронов. Однако в настоящее время нет возможности осуществить с достаточной точностью эталон, опирающийся на такое определение. Вследствие этого пришлось отказаться от единицы количества электричества как основной электрической единицы и принять в качестве таковой единицу силы тока - ампер. Размер ампера можно было бы воспроизводить по следующим действиям, которые оказывает ток в окружающей среде:
- по выделению теплоты при прохождении по проводнику;
- по осаждению вещества на электродах при прохождении тока через электролит;
- по пондеромоторным (механическим) действиям тока на магнит или проводник с током.
В 1893 г. Международный конгресс электриков в Чикаго принял первый эталон силы электрического тока - ампер, установив так называемый международный ампер. Ампер воспроизводился с помощью серебряного вольтметра и имел следующее определение: международный ампер – неизменяющийся ток, который проходя через водный раствор азотнокислого серебра, при соблюдении приложенной спецификации выделяет 0,001118 г серебра в 1 с.
IX Генеральная конференция по мерам и весам в 1948 г. приняла следующее определение ампера: “Ампер - сила неизменяющегося тока, который, проходя по двум параллельным проводникам бесконечной длины и ничтожно малой площади круглого поперечного сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызывал бы между этими проводниками силу взаимодействия, равную 2·10-7 Н на каждый метр длины”. Это определение позволило получить наилучшую точность воспроизведения ампера.
Приведенная формулировка содержит понятие бесконечно тонких и бесконечно длинных проводников, которые на практике осуществить невозможно. Однако, на основе закона Ампера можно рассчитать с достаточной степенью точности силу взаимодействия токов, протекающих по проводникам конечных размеров.
В качестве эталона ампера были приняты токовые весы (рис. 1.6).
Токовые весы представляют собой рычажные равноплечие весы, в которых подвешенная слева подвижная катушка уравновешивается грузом, положенным на правую чашку весов. Подвижная катушка входит во вторую неподвижную коаксиально расположенную катушку. При прохождении по этим последовательно соединенным катушкам постоянного электрического тока подвижная катушка опускается, поэтому на правую чашку весов следует положить добавочный груз. В соответствии с законом Ампера сила взаимодействия токов в катушках будет равна
F=kI 1 I 2 =kI 2,
где I 1 =I 2 =I - сила тока в катушках;
k - коэффициент пропорциональности, зависящий от формы и размеров катушек, принятого значения относительной магнитной проницаемости среды и др.
С другой стороны, в соответствии со вторым законом Ньютона
F = mg,
где m - масса уравновешивающего груза;
g - ускорение свободного падения в месте расположения весов.
Приравнивая эти выражения, получаем расчетную формулу для силы
тока
.
Государственный первичный эталон ампера представляет собой комплекс измерительных средств в следующем составе.
Рисунок 1.6 - Токовые весы
1. Токовые весы с гирей массой 8,16044 г и с дистанционным управлением.
2. Аппаратура для передачи размера единицы, в которую входит катушка сопротивления Р342, получившая свое значение от первичного эталона Ома.
Погрешность воспроизведения размера единицы тока не превышает 0,001%. Эталон находится в ГП “ВНИИМ им. Д.И. Менделеева”,
г. С.-Петербург.
В связи с успехами квантовой метрологии появилась возможность воспроизводить единицу силы тока более точно с помощью косвенных измерений в соответствии с выражением I = U/r. При этом размер единицы U электрического напряжения – вольт - воспроизводится с помощью квантового эффекта Джозефсона (пп. 1.4.1), а размер единицы r электрического сопротивления – ом – с помощью квантового эффекта Холла (пп. 1.4.2). Среднеквадратическое отклонение косвенного воспроизведения ампера составляет 5×10-8, а неисключенная систематическая погрешность - 2×10-7. Таким образом, погрешность воспроизведения ампера возросла более чем на два порядка.
1.3.5 Эталон единицы температуры 
Измерения температуры Т с момента изобретения термометра основывались на применении того или иного термометрического вещества, изменяющего свой объем или давление при изменении температуры. Отсчет температуры в этих случаях осуществляется по равномерной шкале
,
где 
- соответственно отсчет по шкале термометра и положения реперных точек 
. В качестве реперных (опорных) точек выбирали точки калибровки термометра, соответствовавшие температурам перехода термометрического вещества из одного агрегатного состояния в другое (температуры плавления и кипения). В этих точках температура вещества остается постоянной все время пока осуществляется переход.
В 1715 г. Фаренгейт создал ртутный термометр и предложил для построения термодинамической шкалы две точки: температуру смеси льда с солью и нашатырем, которую он обозначил 0, и температуру тела человека, которую он обозначил числом 96.
Шкала Реомюра (1736 г.) имеет две постоянные точки, более удобные для воспроизведения: точку таяния льда 0 и точку кипения воды 80 град.
Шкала Цельсия имеет те же реперные точки, что и шкала Реомюра, только расстояние между ними делится на 100 градусов. Показания термометров зависели от рода термометрического вещества и условий его теплового расширения (рис. 1.7).
Томсон (Кельвин) показал, что можно установить температурную шкалу, которая не зависит от рода термодинамического вещества. Единственной реперной точкой в ней предлагалось сделать тройную точку воды, (точка равновесия воды в твердой, жидкой и газообразной фазах).
Рисунок 1.7 - Температурные шкалы
Эта точка может быть воспроизведена с точностью 0,0001 оС. Схема сосуда, воспроизводящего тройную точку воды, изображена на рис. 1.8. За температуру реперной точки была принята температура 273,16 К, что на 0,01 градус больше температуры таяния льда. Один кельвин это 1/273,16 части термодинамической температуры тройной точки воды. Остальная шкала должна была строиться на основании формулы
,
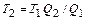где Q 1 - количество тепла, получаемого от нагревателя любымтелом;
Q 2 - количество тепла, отдаваемого телом холодильнику при обратимом цикле Карно;
T 1 и T 2- температуры нагревателя и холодильника, причем температуре T 2придают значение тройной точки воды. В этом случае для определения температуры Т 1 необходимо знать лишь отношение количеств теплоты.
Воспроизведение термодинамической шкалы температур представляет большую трудность. Поэтому IX Генеральная конференция по мерам и весам в 1948 г. установила практическую температурную шкалу, воспроизводимую по определенным постоянным реперным точкам. Температура в реперных точках определяется газовым термометром, использующим соотношение между объемом, давлением и температурой идеального газа. Это наиболее точные, но очень трудоемкие измерения, выполняемые лишь в немногих ведущих метрологических лабораториях мира. Основная сложность их состоит в учете несоответствия реального газа идеальному.
В 1968 г. XIII Генеральная конференция по мерам и весам установила 12 реперных точек в диапазоне от 13,8 К – тройная точка водорода до 1337,58 K– точка затвердевания золота. В промежутках между репернымиточками значения температуры воспроизводятся с помощью эталонных термометров, использующих свойства расширения тел или изменения их сопротивления и т.п. В 1990 г. международная практическая шкала температур (МТШ-90) была уточнена и расширена (от 0,65 К - давление насыщенных паров 3He и 4He до 1357,77 – точка плавления меди).
Рисунок 1.8 - Схема сосуда, воспроизводящего тройную точку воды
Среднеквадратическое отклонение воспроизведения кельвина в этом диапазоне составляет от 5×10-4 до 10-2 при неисключенной систематической погрешности 3×10-3.
В Харьковском ГНПО “Метрология” создан государственный эталон для воспроизведения температуры на основе плазменных источников излучения в диапазоне 10000-150000 К со среднеквадратическим отклонением не более 3.10-2.
