Математические модели позволяют оценивать характеристики ошибок в программах и прогнозировать их надежность при создании и эксплуатации. Модели имеют вероятностный характер, и достоверность прогнозов зависит от точности исходных данных и глубины прогнозирования по времени. Эти математические модели предназначены для оценки:
- показателей надежности комплексов программ в процессе отладки;
- количества ошибок, оставшихся невыявленными;
- времени, необходимого для обнаружения следующей ошибки в функционирующей программе;
- времени, необходимого для выявления всех ошибок с заданной вероятностью.
Использование моделей позволяет эффективно проводить отладку и испытания комплексов программ, помогает принять рациональное решение о времени прекращения отладочных работ.
В настоящее время используется множество различных математических моделей, основными из которых являются:
1) экспоненциальная модель изменения ошибок в зависимости от времени отладки;
2) модель, учитывающая дискретно - понижающуюся частоту появления ошибок как линейную функцию времени тестирования и испытаний;
3) модель, базирующаяся на распределении Вейбула;
4) модель, основанная на дискретном гипергеометрическом распределении.
При обосновании математических моделей выдвигаются некоторые гипотезы о характере проявления ошибок в комплексе программ.
Наиболее обоснованными представляются предположения, на которых базируется первая экспоненциальная модель изменения ошибок в процессе отладки и которые заключаются в следующем:
1) любые ошибки в программе являются независимыми и проявляются в случайные моменты времени;
2) время работы между ошибками определяется средним временем выполнения команды на данного аппаратного средства и средним числом команд, исполняемым между ошибками. Это означает, что интенсивность проявления ошибок при реальном функционировании программы зависит от среднего быстродействия аппаратного средства;
3) выбор отладочных тестов должен быть представительным и случайным, с тем чтобы исключить концентрацию необнаруженных ошибок для некоторых реальных условий функционирования программы;
4) ошибка, являющаяся причиной искажения результатов, фиксируется и исправляется после завершения тестирования либо вообще не обнаруживается.
Из этих свойств следует, что при нормальных условиях эксплуатации количество ошибок, проявляющихся в некотором интервале времени, распределено по закону Пуассона. В результате длительность непрерывной работы между искажениями распределена экспоненциально.
Предположим, что в начале отладки комплекса программ при 
в нем содержалось 
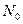ошибок. После отладки в течении времени 
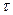осталось 
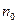ошибок и устранено 
ошибок (
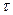). При этом время соответствует длительности исполнения программ на вычислительной системе (ВС) для обнаружения ошибок и не учитывает простои машины, необходимые для анализа результатов и проведения корректировок.
Интенсивность обнаружения ошибок в программе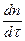 
и абсолютное количество устранённых ошибок связываются уравнением
, (3.11)
где 
– коэффициент пропорциональности.
Если предположить, что в начале отладки при отсутствуют обнаруженные ошибки, то решение уравнения (3.11) имеет вид
,
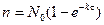а количество оставшихся ошибок в комплексе программ
,
и пропорционально интенсивности обнаружения 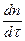с точностью до коэффициента .
Среднее время безотказной работы программ до отказа или наработка на отказ, который рассматривается как обнаруживаемое искажение программ, данных или вычислительного процесса, нарушающее работоспособность, равно величине, обратной интенсивности обнаружения отказов (ошибок)
.
Если учесть, что до начала тестирования в комплексе программ содержалось 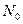ошибок и этому соответствовала наработка на отказ 
, то функцию наработки на отказ от длительности проверок можно представить в следующем виде
.
Если известны моменты обнаружения ошибок 
и каждый раз в эти моменты обнаруживается и достоверно устраняется одна ошибка, то, используя метод максимального правдоподобия, можно получить уравнение для определения значения начального числа ошибок :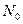
,
а также выражение для расчета коэффициента пропорциональности
.
В результате можно рассчитать число оставшихся в программе ошибок и среднюю наработку на отказ, т.е. получить оценку времени до обнаружения следующей ошибки.
Если в процессе отладки и испытаний программ для повышения наработки на отказ от значения 
до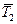 
необходимо обнаружить и устранить 
ошибок, то величина определяется соотношением
.
Выражение для определения затрат времени 
на проведение отладки, которые позволяют устранить ошибок и соответственно повысить наработку на отказ от значения от до 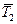, имеет вид:
.
Вторая модель построена на основе гипотезы о том, что частота проявления ошибок (интенсивность отказов) линейно зависит от времени испытания между моментами обнаружения последовательных 
и 
ошибок.
,
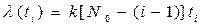где 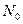- начальное количество ошибок;
– коэффициент пропорциональности, обеспечивающий равенство единице площади под кривой вероятности обнаружения ошибок.
Для оценки наработки на отказ получается выражение, соответствующее распределению Релея:
,
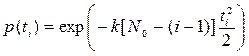где 
.
Отсюда плотность распределения времени наработки на отказ
.
Использовав функцию максимального правдоподобия, получим оценку для общего количества ошибок 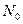и коэффициента
;
.
Особенностью третьей модели является учет ступенчатого характера изменения надёжности при устранении очередной ошибки. В качестве основной функции рассматривается распределение времени наработки на отказ. Если ошибки не устраняются, то интенсивность отказов является постоянной, что приводит к экспоненциальной модели для распределения:
;
.
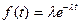Для аппроксимации изменения интенсивности от времени при обнаружении и устранении ошибок используется функция следующего вида
.
Если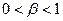 
, то интенсивность отказов снижается по мере отладки или в процессе эксплуатации. При таком виде функции плотность 
функции распределения наработки на отказ описывается двухпараметрическим распределением Вейбулла, которое достаточно хорошо отражает реальные зависимости при расчете функции наработки на отказ:
.
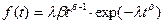