Перевод чисел из десятичной системы в двоичную, восьмеричную и шестнадцатеричную более сложен и может осуществляться различными способами. Рассмотрим один из алгоритмов перевода на примере перевода чисел из десятичной системы в двоичную, при этом необходимо учитывать, что алгоритмы перевода целых чисел и правильных дробей будут различаться.
Алгоритм перевода целого десятичного числа в двоичное будет следующим:
1. Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы (на 2) до тех пор, пока не получим частное меньше делителя, т.е. меньше 2.
2. Получить искомое двоичное число, для чего записать полученные остатки в обратной последовательности. В качестве примера рассмотрим перевод десятичного числа 19 в двоичную систему, записывая результаты в таблицу:

В результате получаем двоичное число:
А2 = a4a3a2a1a0 = 100112.
Алгоритм перевода десятичной дроби в двоичную будет следующим:
1. Последовательно выполнять умножение исходной десятичной дроби и получаемых дробей на основание системы (на 2) до тех пор, пока не получим нулевую дробную часть или не будет достигнута требуемая точность вычислений.
2. Получить искомую двоичную дробь, записав полученные целые части произведения в прямой последовательности. В качестве примера рассмотрим перевод десятичной дроби 0,75 в двоичную систему, записывая результаты в таблицу:
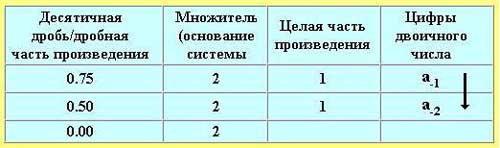
В результате получаем двоичную дробь:
А2 = 0,а-1a-2 = 0,112.
Рассмотрим алгоритм перевода целых чисел на примере перевода целого десятичного числа 424 в шестнадцатеричную систему, т.е. из системы счисления с основанием р = 10 в систему счисления с основанием q = 16. В процессе выполнения алгоритма необходимо обратить внимание, что все действия необходимо выполнять в исходной системе счисления (в данном случае десятичной), а полученные остатки записать цифрами новой системы счисления (в данном случае шестнадцатеричной).

В результате получаем шестнадцатеричное число:
А16 = а2a1a0 = 1А816.
Рассмотрим теперь алгоритм перевода дробных чисел на примере перевода десятичной дроби 0,40625 в восьмеричную систему, т.е. из системы счисления с основанием р = 10 в систему счисления с основанием q= 8. В процессе выполнения алгоритма необходимо обратить внимание, что все действия необходимо выполнять в исходной системе счисления (в данном случае десятичной), а полученные остатки записать цифрами новой системы счисления (в данном случае восьмеричной).

В результате получаем восьмеричную дробь:
А8 = а-1а-2 = 0,328
Перевод чисел, содержащих и целую и дробную часть, производится в два этапа. Отдельно переводится по соответствующему алгоритму целая часть и отдельно – дробная. В итоговой записи полученного числа целая часть от дробной отделяется запятой.






