Пример. 8.1. Потребители, какой категории можно запитать от ниже приведённых СЭС?
| Рис. 5.11. Варианты схемы электроснабжения ГПП: G – источник питания; Q, Q1 – выключатели; Л – линия электропередачи; QR – отделитель; QK – короткозамыкатель; Т – трансформатор; (1 – 6) – цифровое обозначение электрооборудования |
Рис. 4-20. Схема присоединения подстанций (6 – 10) кВ
Рис. 3.2. Принципиальная схема резервирования цеховых сетей по ВН
за счёт применения двойных "сквозных" магистралей:
а – простая магистраль; б – двойная "сквозная" магистраль
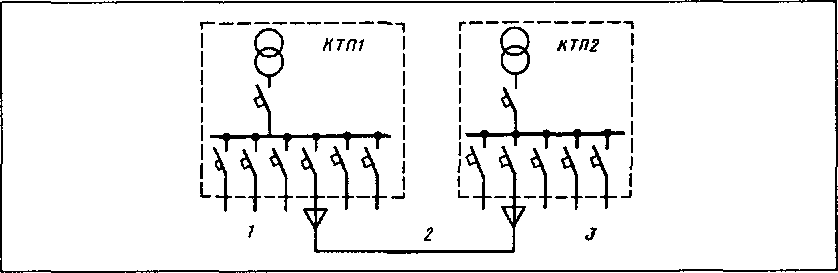
Рис. 3.3. Принципиальная схема резервирования цеховых сетей
по НН за счёт применения перемычки с АВР:
1 – потребители; 2 – резервирующая перемычка
|
Рис. 3.4.Взаимное резервирование питающих магистралей:
КТП – комплектные трансформаторные подстанции
Рис. 5.2. Схема радиального питания:
а – группы РП с резервированием от второго источника; б – одного РП от двух источников;
в – обособленной однотрансформаторной подстанции по одиночной линии (по двухкабельной линии)
|
Рис. 5.3. Двойная магистральная схема с односторонним питанием
при отсутствии сборных шин на цеховых ТП
9. Структурное обеспечение надёжности.
Пример 9.1. Составить структурные схемы для задач предшествующего раздела
10. Структурное обеспечение надёжности.
Пример 10.1. Определить среднее время восстановления Т в и интенсивность отказов СЭС λ с
|
| |
10а. Невзаиморезервированные источники питания
Задача 9.4. Потребитель получает электроэнергию по линиям электропередачи Л1 и JI2, отказы которых независимы. Каждая линия пропускает всю необходимую потребителю мощность. Параметры потоков отказов линий и средние времена восстановления приведены в табл. 9.2.
Таблица 9.2.
Параметры надежности схемы электропередач
| Показатель надёжности | Элемент сети | |
| Л1 | Л2 | |
| λ, 1/год | 0,03 | 0,04 |
| Т в, ч |
Определить параметр потока отказов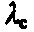 
системы, среднюю вероятность отказа 
системы и среднее время 
ее восстановления (преднамеренные отключения не учитывать).
Решение. Параметр потока отказов системы с двумя параллельно соединенными элемента-ми
Средняя вероятность отказа системы равна произведению вероятностей событий отказа элементов системы при их независимости:
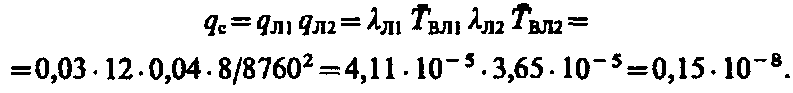
Среднее время восстановления системы
Задача 9.5. Решить предыдущую задачу при условии, что каждая линия пропускает только 50 % мощности, требуемой потребителю (рис. 9.4). Дополнительно определить вероятность получения потребителем лишь 50 % мощности.
Решение. Поскольку под отказом системы понимают исчезновение напряжения в узле нагрузки, параметр потока отказов этой системы, средняя вероятность ее отказа и среднее время восстановления будут те же, что и в предыдущей задаче, т. е.
| Рис. 9. 4. Схема системы передачи электроэнергии |
При пропускной способности каждой линии лишь 50 % мощности нагрузки существует вероятность выдачи потребителю лишь 50 % требуемой мощности.
Если рассматривать отказ системы как получение потребителем 50 % мощности, то параметр потока отказов 
такой системы определяется вероятностью работы только одной линии:
При этом средняя вероятность отказа 
системы
Среднее время восстановления системы, способной передать 50 % мощности нагрузки
Анализ результатов решения задач 9.4, 9.5 показывает:
Вероятность отказа резервированной системы с линиями 100 %-й пропускной способности достаточно низкая (
), что позволяет при реальном проектировании осуществлять питание потребителей I и II категорий надежности по двум линиям.
При 50 %-й пропускной способности каждой линии вероятность неполучения потребителем 100 % мощности резко возрастает (
), так что надежность такой системы недостаточна для электроснабжения потребителей I и II категорий надежности. Поэтому в резервированных системах пропускная способность каждого элемента составляет, как правило, 100 % мощности нагрузки, что обеспечивает ее выдачу при аварийном отключении одной линии.
11. Количество резервных трансформаторов на складе.
Федосенко Р. Я. Трансформатор в местной распределительной электрической сети. –
М.: Издательство министерства коммунального хозяйства РСФСР, – 1963.
Пример 11.1. Пусть в организация эксплуатирует 200 трансформаторов. СЭС
При существующей надежности трансформаторов их нужно резервировать путем складского централизованного резерва, что и предписывается ПУЭ для потребителей II и III категорий.
При развитой сети до 1000 В желательно иметь резервирование от соседних ТП. При этом ясно, что специально резерв по мощности создавать не следует, а резервирующие трансформаторы в аварийном режиме могут быть загружены до (1,8 – 2,0) S н номинальной мощности.
Весьма важно для эксплуатационника знать, сколько трансформаторов следует иметь на складе, чтобы обеспечить замену поврежденных. Рассмотрим вначале случай, когда предприятие получает трансформаторы один раз в год и не ремонтирует поврежденные.
Эксплуатационный инженер знает, сколько в среднем трансформаторов повреждается ежегодно. Пусть из 200 трансформаторов, эксплуатируемых в сети, ежегодно из-за повреждений приходится заменять 4. Для простоты примем, что резервный трансформатор может быть включен вместо любого из 200 трансформаторов.
Если на складе будет 4 трансформатора, то может случиться, что в этот год будет повреждено более четырех. Тогда у эксплуатационного инженера не хватит трансформаторов для замены. На среднюю цифру здесь ориентироваться нельзя, так как от нее всегда могут быть отклонения. Это надо предусмотреть. Надо определить, сколько может повредиться трансформаторов, если в среднем ежегодно повреждалось 4.
Задача может быть решена с помощью методов теории вероятностей. Поверждения трансформаторов – события случайные. Они могут быть, а могут и не быть. Кроме того, повреждения бывают редко (один раз в 50 и более лет), а вероятность повреждений весьма мала. Такие события подчиняются закону редких событий.
Вероятность повреждения ровно n трансформаторов при среднем числе А будет: 
где n! – факториал числа n [ n! = n (n –1)∙(1 – 2)…2∙1; 0! = 1].
Определим вероятность выхода из работы в данном году ровно 0, 1,2... n трансформаторов, если в среднем ежегодно повреждается A = 4. Вычисления сведем в табл. 23.
Таблица 23
| n | Р r (n, 4) | F r (n, 4) | n | Р r (n, 4) | F r (n, 4) |
| 0,0183 | 0,0183 | 0,0696 | 0,9489 | ||
| 0,0733 | 0,0916 | 0,0297 | 0,9786 | ||
| 0,1465 | 0,2381 | 0,0133 | 0,9919 | ||
| 0,1954 | 0,4335 | 0,0053 | 0,9972 | ||
| 0,1953 | 0,6288 | 0,0025 | 0,9997 | ||
| 0,1563 | 0,7851 | 0,0003 | 1,0000 | ||
| 0,1042 | 0,8893 | - | - | - |
Во второй графе таблицы приведены вероятности ровно n повреждений трансформаторов. Например, вероятность иметь ровно 10 поврежденных трансформаторов составляет 0,00553; вероятность не иметь поврежденных трансформаторов равна 0,0183, т. е. около двух шансов из ста.
Нас интересует вероятность иметь не ровно n повреждений, а n и менее или, что то же самое, – не более 
поврежденных трансформаторов. Для этого надо просуммировать вероятности, приведенные во второй графе табл. 23. Тогда вероятность того, что за год повредится n и менее трансформаторов, если в среднем повреждается А, может быть определена из выражения:
(23)
В графе 3 табл. 23 рассчитаны эти вероятности. Вероятность того, что в данном году будет повреждено не более 4 трансформаторов равна 0,6288. Если бы эксплуатационный инженер имел на складе четыре трансформатора, то потребность в них была удовлетворена примерно в 63 % случаев. В остальных 37 % случаев заменить поврежденные трансформаторы было бы нечем. При четырех трансформаторах на складе и среднем числе повреждающихся трансформаторов A = 4 обеспеченность резервом составила бы только 63 %, что было бы недостаточно. Достаточной обеспеченностью резервом можно считать 99 %. Следовательно, надо рассчитывать на повреждение такого числа трансформаторов, вероятность которого составляет:
В нашем случае (A = 4) надо рассчитывать на 9 трансформаторов, что следует из табл. 23 при A = 4, F r (9,4) = 0,9919.
Из уравнения (23) следует, что число резервных трансформаторов, казалось бы, не зависит от общего числа трансформаторов, эксплуатируемых в сети. Оно зависит от числа трансформаторов, которые в среднем приходится заменять из-за повреждений. Ясно, что, чем больше трансформаторов эксплуатируется сетью, тем больше их повреждается и тем больше трансформаторов надо иметь в резерве. Но прямой зависимости здесь не имеется. Нельзя сказать, что в резерве нужно всегда иметь, например, 5 или10 % трансформаторов. Если в сети работает от 1 до 5 трансформаторов, в резерве на складе надо иметь все равно один трансформатор, т. е. от 100 до 20 % резервных трансформаторов. Если в сети эксплуатируется 1000 трансформаторов, а в среднем ежегодно повреждается 5, то резерв должен составить не более 12 трансформаторов, или 1,2 %.
Таблица 24
Резерв трансформаторов и его обеспеченность
| Среднее число ежегодно заменяемых трансформаторов | Резерв (число) трансформаторов при обеспеченности, % | Среднее число ежегодно заменяемых трансформаторов | Резерв (число) трансформаторов при обеспеченности, % | ||||||||||
| 0,1 | 3,5 | ||||||||||||
| 0,2 | 4,0 | ||||||||||||
| 0,3 | 4,5 | ||||||||||||
| 0,4 | 5,0 | ||||||||||||
| 0,5 | 5,5 | ||||||||||||
| 0,6 | 6,0 | ||||||||||||
| 0,8 | 6.5 | ||||||||||||
| 1,0 | 7,0 | ||||||||||||
| 1,5 | 8,0 | ||||||||||||
| 2,0 | 9,0 | .14 | |||||||||||
| 2,5 | 10,0 | ||||||||||||
| 3,0 | - | - | - | - | - | - | - |
В табл. 24 на основании формулы (23) приведены данные по определению числа резервных трансформаторов, необходимых сети для замены поврежденных.
Приведенное в графе 1 табл. 24 среднее число трансформаторов, которые приходится заменять, определяется по опыту работы сети или сетевого объединения. Эти данные надо оценить, найти ошибку среднего числа поврежденных трансформаторов по выражению:
где t α – нормированное отклонение (t α = 2);
А – среднее число повреждаемых в год трансформаторов сети;
N – число эксплуатируемых трансформаторов. Например, в сети, где эксплуатируется 200 трансформаторов, за 4 года ежегодно повреждалось 2, 9, 5 и 8. В среднем
средняя за 4 года повреждаемость
Средняя ошибка в определении среднего за 4 года числа поврежденных трансформаторов:
или
Средняя определена с большей надежностью, поэтому следует ориентироваться
на 6 трансформаторов, которые могут в среднем повредиться за один год.
В остальных графах табл. 24 приведены числа трансформаторов, которые надо иметь в резерве при заданной обеспеченности. В нашем случае для того, чтобы обеспеченность резерва составила 99 %, необходимо иметь 12 резервных трансформаторов (6 % от общего числа). Более 14 резервных трансформаторов или более 7 % держать на складе не имеет смысла. Они не будут использованы, а их стоимость только увеличит затраты на передач) энергии.
Анализируя формулу (23) и данные табл. 24, можно придти к выводу о большой выгоде централизации резерва. Рассмотрим два случая.
Пусть в области имеется 40 электросетей и в каждой эксплуатируется по 20 трансформаторов. Повреждаемость трансформаторов одинакова и равна 0,01 трансформатора в год.
В среднем в каждой сети ежегодно повреждается:
трансформатора.
Тогда в каждой сети надо иметь по два трансформатора при обеспеченности резерва 99 %. Во всех 40 электросетях следует иметь 2∙40 = 80 резервных трансформаторов или 10 % от общего числа эксплуатируемых.
Если в области создать централизованный резерв, то в сред нем будет необходимо заменить те же А = 0,01∙800 = 8 трансформаторов. Резерв, при той же обеспеченности 99 %, составит только 15 трансформаторов или 1,88 %. Централизация резерва в этом случае позволяет снизить потребность в трансформаторах на 65 ед. Целесообразность централизованного резерва бесспорна. Причём эти 15 трансформаторов территориально могут быть рассредоточены для удобства их транспортировки.
В табл. 24 приведены данные о числе резервных трансформа торов при среднем числе повреждающихся трансформаторов не более 10. В крупных сетевых объединениях их может быть более 10. Тогда число резервных трансформаторов может быть определено по формуле:
(24)
где t α = 1 при обеспеченности резерва 70 %, 1,3 при – 80 %, 1,65 при – 90 %, 2,0 при – 95 %, 2,5 при – 99 % и 3,5 при – 100 %.
Например, в объединении сетей эксплуатируется 10 000 трансформаторов при средней повреждаемости 0,01 трансформатора в год. Обеспеченность резерва должна быть 99%. Тогда в резерве надо иметь:
или 1,25 % общего числа эксплуатируемых трансформаторов.
Ясно, что не следует ежегодно планировать получение всего количества резервных трансформаторов. Надо планировать получение только такого числа заменяемых трансформаторов, при которых резерв будет обеспечен. Примерно это равно среднему числу повреждаемых трансформаторов А. Применительно к рассмотренным случаям: для сети с 20 трансформаторами надо планировать получение 2 резервных трансформаторов за 10 лет. Для объединения с 800 эксплуатируемыми трансформаторами надо планировать ежегодно получение примерно 8 трансформаторов, а около 7 трансформаторов останется от прошлых лет. Для объединения, эксплуатирующего 10 000 трансформаторов, необходимо ежегодно получать 100 трансформаторов. В масштабе республики или страны необходимо планировать число резервных трансформаторов, соответствующее их средней повреждаемости за (4 – 5) лет. Это около 1 % эксплуатируемых трансформаторов I и II габаритов, так как средняя повреждаемость их около 0,01. Если же ориентироваться на средний расчетный срок службы 20 лет, то надо планировать замену 5 % эксплуатируемых трансформаторов.
Таково решение задачи в случаях, когда поврежденные трансформаторы не возвращаются в данном году в эксплуатацию.
Если поврежденные трансформаторы ремонтируются или заменяются на исправные на заводе централизованного обезличенного ремонта, то принципиальное решение задачи останется прежним. Изменится лишь ожидаемое число поврежденных трансформаторов, которое надо учитывать в уравнениях (23) и (24). Оно будет меньше. Если за 36 дней трансформатор может быть отремонтирован или заменен на исправный на заводе централизованного ремонта, то ожидаемое число поврежденных трансформаторов, на которое следует ориентироваться при создании резерва, уменьшится в 10 раз.
Например, если ежегодно приходится заменять 4 поврежденных трансформатора, то эксплуатационный инженер должен ориентироваться на ожидаемое число поврежденных трансформаторов, равное 4:10 = 0,4. Тогда на складе должно быть не менее 2 трансформаторов при обеспеченности 99 % или один трансформатор при обеспеченности 90 и 95 %. Эти данные следуют из табл. 24.
Ускорение ремонта трансформаторов позволяет резко сократить необходимый резерв. Так, если рассчитывать на получение трансформаторов для резерва один раз в год, то при обеспеченности 99 % надо получать 9 трансформаторов (А = 4 ед/год). Если же поврежденные трансформаторы возвращаются в сеть через 1,5 месяца, то ожидаемое число повреждаемых трансформаторов за этот период составит лишь А = 0,4, а на складе надо будет держать лишь 2 исправных трансформатора.
Выше было принято, что трансформаторы равномерно повреждаются в течение года. Это не всегда так. В воздушных сетях, например, трансформаторы более часто повреждаются в грозовой период. Эксплуатационный инженер по опыту работы своей сети может оценить среднее число трансформаторов, которое может быть повреждено за (1,5 – 3) месяца и определить по табл. 24 необходимое число резервных трансформаторов.
Отметим, что приведенная методика пригодна для определения резерва любого оборудования (кабелей, выключателей, трансформаторов тока и напряжения, плавких вставок и т. д.).
Весьма полезна она также и для определения числа дежурного персонала оперативных служб электросети.
Закон распределение Пуассона.
Этот закон позволяет определить вероятность 
наступления случайного события A (отказов) ровно m за промежуток времени t:
, 
, 
,
где a = λt – параметр закона распределения Пуассона – математическое ожидание числа событий за время t; 
– интенсивность случайного события (отказов).
Закон распределения Пуассона может быть получен из биномиального распределения при достаточно больших n и малых р тогда
.
Другим важным свойством закона Пуассона является то, что он является предельным для биномиального распределения:
Pmn = Cmn· Pm· (1− P)(n – m ), (3.11)
если одновременно устремлять число опытов n к бесконечности, а вероятность Р – к нулю, причем их произведение nр сохраняет постоянное значение:
nр = а. (3.12)
Это предельное свойство биномиального распределения можно записать в виде:
(3.13)
Предельное свойство биномиального закона часто находит применение на практике. Допус-тим, что производится большое количество независимых опытов n, в каждом из которых событие А имеет очень малую вероятность Р. Тогда для вычисления вероятности Pnm того, что событие А появится равно m раз, можно воспользоваться приближенной формулой
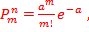(3.14)
где nр = а – параметр закона Пуассона, которым приближенно заменяется биномиальное распреде-ление.
