Закон распределение Пуассона
Этот закон позволяет определить вероятность 
наступления случайного события A (отказов) ровно m за промежуток времени t:
, 
, 
,
где a = λt – параметр закона распределения Пуассона – математичес-
кое ожидание числа событий за время t;
λ – интенсивность случайного события (отказов).
Закон распределения Пуассона может быть получен из биномиального распределения при достаточно больших n и малых р тогда
.
Биномиальное распределение
Если производится серия n независимых опытов, причём вероятность появления изучаемого случайного события A в каждом опыте постоянна и равна р, а вероятность его непоявления равна 
, то вероятность 
появления данного события точно m раз равна
где 
Пример № 1. В распределительном пункте (РП) установлено пять автоматических выключателей. Нормальная работа потребителей обеспечивается при их исправном состоянии. При монтаже РП выключатели выбирались из партии объемом в 1000 штук, в которой было 950 исправных выключателей и 50 не исправных. Найти вероятность исправной работы РП.
Решение. Число элементарных событий 
,
Обозначим: событие А есть исправная работа РП, оно осуществляется если все выключате-ли выбраны из числа исправных.
Число элементарных событий, благоприятствующих событию А, равно 
. Следовательно, 
При одновременном изучении двух или нескольких событий различают события совмест-ные и несовместные.
2. Федосенко Р. Я. Трансформатор в местной распределительной электрической сети. –
М.: Издательство министерства коммунального хозяйства РСФСР, – 1963.
Пример №2. Известно (из опыта работы), что удельная повреждаемость (интенсивность отказов) трансформаторов (6 – 10)/0,4 кВ конкретной мощности равна λ = 0,02 [1/год] повреждения за t = 1 год, т. е. в среднем повреждаются (наступает отказ) 2 трансформатора из 100 работающих в данной сети. Принимаем её неизменной в течение всего срока службы трансформатора
Параметр закона Пуассона за год a = λt = 0,02∙1 = 0,02 [о.е.].
Параметр закона Пуассона за десять лет a = λt = 0,02∙10 = 0,2 [о.е.].
Вероятность наступления случайного события A ровно m отказов за промежуток времени t, и заключающееся в том, что трансформатор не повредится за год (m = 0 – число повреждений равно нулю) составляет
т. е. 98 шансов из 100 за то, что трансформатор, питающий данного потребителя, не повредится, а 2 шанса, что будут перерывы питания.
Вероятность иметь ровно один отказ трансформатора в год (m = 1, λ = 0,02[1/год],
t = 1 год и a = λt = 0,02∙1 = 0,02 [о.е.])
ничтожно мала.
Вероятность иметь более одного повреждения (m > 1, λ = 0,02[1/год], t = 1 год и
a = λt = 0,02∙1 = 0,02 [о.е.]) составит:
0,0004.
Отметим, что если после первого повреждения трансформатор заменили, то с такой же вероятностью, равной 0,02, можно ожидать повреждения вновь установленного трансформатора.
Посмотрим, как изменяются значения вероятностей перерывов питания за t = 10 лет.
В этом случае среднее число повреждений λ = 10∙0,02 = 0,2, и a = λt = 0,02∙10 = 0,2 [о.е.], а вероятности не иметь отказ (m = 0) или иметь m = 1, m = 2, m = 3 отказов соответственно равна:
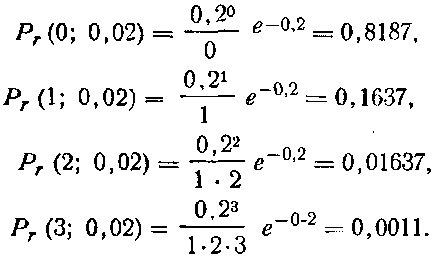
Анализируя эти цифры, можно видеть, что около 82 шансов из 100 за то, что трансформатор не повредится и, следовательно, перерыва в питании потребителей не будет, а 18 шансов за то, что перерывы питания будут; 16 шансов свидетельствуют о том, что произойдет только один перерыв, и около 2 шансов, что будет два и более перерывов.
На основе закона редких событий в основной части книги решается задача определения числа повреждений трансформаторов в сети.
3. Волков Н. Г. Надёжность электроснабжения. Учеб. пособие/ Том. политех. ун-т. – Томск, 2003. – 140 с.
Пример №3. Силовой трансформатор в городской электрической сети работает в течение времени Т, которое является случайной величиной и распределено по показательному закону с плотностью:
где λ = 0,03 1/год.
По истечении времени Т вследствие роста нагрузки, повреждения его или других причин трансформатор заменяют другим.
Поставим два блока вопросов.
1. Определить:
– среднюю продолжительность эксплуатации трансформатора;
– вероятность надёжной работы трансформатора в течение первых 10 лет;
– вероятность отказа трансформатора в период между 10 и 20 годами эксплуатации.
2. Определить вероятность того, что за время эксплуатации
t = 30 годам:
– трансформатор не понадобится заменять ни разу;
– трансформатор потребуется заменить два раза;
– трансформатор потребуется заменить не менее двух раз.
