Расчёт надёжности программных средств

 

В составе современных технических систем всё больший удельный вес занимают средства вычислительной техники. Стоимость основной ячейки интегральных микросхем – логического вентиля – с развитием электроники непрерывно снижается. Напротив, программное обеспечение, удельная стоимость которого у первых ЭВМ была очень малой, в настоящее время составляет более 90 % стоимости компьютеров. Этот рост стоимости объясняется несколькими причинами:

1) Технология создания программного обеспечения серьезно отстаёт от технологии производства элементной базы;

2) по своей природе программное обеспечение сложнее оборудования (объём программ для современных систем оценивается в 10⁶ – 10⁸ и более команд или информационных слов);

3) требования к программному обеспечению в течение его жизненного цикла, который увеличился до 15 – 20 лет, существенно изменяются;

4) в отличие от комплекса технических средств для программного обеспечения (ПО) очень трудно рассчитать на этапе проектирования достижимое быстродействие, кроме того, в оборудование непрерывно вносятся изменения.

Отсюда следует, что в процессе создания и эксплуатации ПО непрерывно изменяется, а самим программам свойственны ошибки. В самом общем виде под ошибкой понимают любое не выполнение программой функций, которые заданы техническим заданием. Проявление ошибки является отказом, а надёжность вычислительной техники состоит из двух составляющих: надёжности технических средств и надёжности программного обеспечения.

Приближенно можно полагать, что отношение числа ошибок в программе к общему числу команд в ней лежит в диапазоне от 0,25 до 10 на 1000 команд. Это означает, что в ПО объёмом в 0,5 млн. команд может быть 125 – 5000 ошибок; причем, такая оценка является оптимистической. Выявление ошибок и их исправление является процессом многоэтапным (в соответствии с этапами «жизни» ПО), трудоёмким и дорогостоящим. По мере перехода к более поздним этапам разработки ПО цена ошибки возрастает, тенденцию этого роста иллюстрирует таблица:

Таблица 2.1 - Примерная «цена» программной ошибки на разных этапах жизни программного обеспечения

Наименование этапа	Стоимость ошибки, руб.
Составление спецификаций
Программирование
Комплексная отладка
Сопровождение ПО у заказчика	350000 - 35000000

 

Цена ошибки, которую не удалось обнаружить на этих этапах, может быть совершенно непредсказуемой и огромной. Свидетельством этого являются аварии, происходящие с космическими аппаратами, многие из которых были потеряны из-за ошибок именно в программном обеспечении.

2.3.1 Основные определения теории надёжности программного обеспечения

Основными терминами, которые используются в теории надёжности программного обеспечения, являются следующие: программная ошибка; число оставшихся в программе ошибок, которые будут переданы далее пользователю; интенсивность обнаружения ошибок (функция риска); «прогон» программы; отказ программы; вероятность безотказной работы программного обеспечения.

Основная трудность определения термина «программная ошибка» состоит в том, что ошибка в программе – это по своей сути функция самой программы и того, чего ожидает от неё пользователь. Перечислим основные проявления, которые можно идентифицировать как ошибку:

- появление при программировании ошибочного операнда или операции;

- несоответствие выполняемых ПО функций требованиям спецификаций, либо ошибка в спецификации, которая приводит к ошибке при выполнении операции ПО;

- ошибки вычислительного характера (например, переполнение);

- исправление ПО, улучшающее его взаимодействие с пользователем.

К программным ошибкам не относят исправления, создающие или уничтожающие временные программные «заглушки» на отсутствующую или не корректную программу, а так же перетрансляцию программы, вызванную накопившимися исправлениями. Количество оставшихся в ПО или переданных ошибок – это потенциальное число ошибок в ПО, которое может быть обнаружено в нём на последующих этапах его жизненного цикла после исправлений, внесённых на данном этапе. Это количество ошибок будем обозначать символом В.

Введём интенсивность обнаружения ошибок или функцию риска r(t), которая определяется отношением числа обнаруженных ошибок к промежутку времени, за который эти ошибки были обнаружены. Для интенсивности обнаружения ошибок справедливы все формулы, которые известны из теории надёжности. В отличие от интенсивности отказов 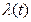функция риска убывает по мере обнаружения и исправления ошибок. Если предположить, что 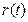остаётся постоянной между моментами обнаружения и исправления ошибок, уменьшаясь скачкообразно на постоянную величину в момент обнаружения ошибок, то для простоты целесообразно полагать её пропорциональной количеству оставшихся ошибок

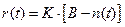, (2.80)

где 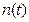- число обнаруженных ошибок на данном этапе.

Дифференцируя уравнение (2.80) по времени получим

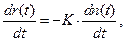
где 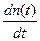- есть функция риска 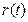. Если решить дифференциальное уравнение 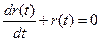, с начальными условиями 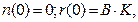то

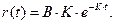(2.81)

Обозначим 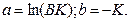Тогда уравнение (2.81) можно переписать в виде

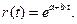(2.82)

Функцию риска зададим дискретно, придав интервалу времени заданное значение (день, неделя, месяц). Логарифмируя уравнение (2.82) для выбранных значений времени 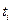, получим систему уравнений вида

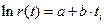(2.83)

Расчёт экспоненциальной регрессии даёт следующие выражения для её коэффициентов

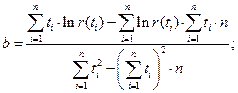(2.84)

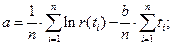(2.85)

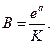(2.86)

Программа для расчёта экспоненциальной регрессии приведена ниже в 2.3.3.

Будем под удельной интенсивностью обнаружения ошибок в ПО понимать следующую функцию времени:

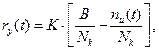(2.87)

где 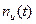- число ошибок в ПО, которые исправлены к моменту времени t; 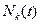- число команд в программе. Приближенно можно полагать, что

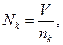(2.88)

здесь 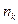- разрядность команды; 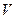- объем программы по Холстеду, что будет; В – число оставшихся ошибок в ПО к моменту t = 0; К – коэффициент пропорциональности. Величины В и К являются неизвестными.

Рассмотрим два периода отладки программы Т₁ и Т₂ такие, что Т₁ < Т₂. Пусть n₁ и n₂ соответственно количество ошибок в ПО, обнаруженных в каждом из периодов. Тогда для среднего времени безошибочной (безотказной) работы в каждом из периодов можно записать следующие выражения:

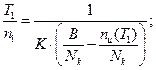(2.89)

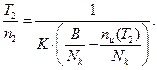(2.90)

Разделив первое равенство на второе, после преобразований можно получить:

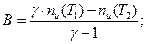(2.91)

где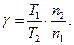

Подставив полученное значение B в формулу для среднего времени безотказной работы в первом периоде отладки программы, можем определить коэффициент пропорциональности

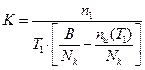. (2.92)

Определив В и К, можно для любого момента времени вычислить значение удельной интенсивности обнаружения ошибок в ПО 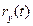и вероятность безотказной работы, полагая, что время исправной работы подчинено экспоненциальному закону распределения.

Прогоном программы называют совокупность действий, включающую в себя:

- ввод возможной комбинации Е_i входных данных;

- выполнение расчёта по программе, которая заканчивается получением результата F(E_i) или отказом.

Для определенного набора входных данных отклонение результата от заданного значения F`(E_i), полученное в результате выполнения программы, находится в допустимых пределах

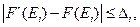(2.93)

а для всех остальных E_i, образующих подмножество 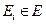, выполнение программы не обеспечивает приемлемого результата, т.е.

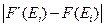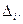> (2.94)

События, описываемые неравенством (2.94), называются отказами программы.

Методика статистической оценки вероятности отказа ПО за n независимых прогонов программы является традиционной и формально включает в себя оценку

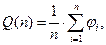(2.95)

где 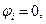если выполняется неравенство (2.93); 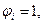если выполняется неравенство (2.94).

Обозначим через 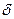допустимую относительную погрешность оценки вероятности отказа. Тогда необходимое число независимых прогонов программы n должно быть пропорционально величин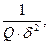е где 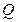- заданное значение вероятности отказа. Так, при 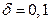и значении 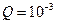число независимых прогонов должно быть не меньше

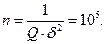
Такое количество прогонов трудно реализовать на практике и обычно обращаются к другим методам оценки вероятности отказа ПО. Зная вероятность отказа, нетрудно вычислить вероятность безотказной работы ПО.

Для проверки надёжности ПО используются методы проверки статистических гипотез и, в частности, последовательный анализ Вальда. Сопоставим дихотомической переменной 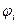значение 1, если выполняется (2.94), и значение 0, если выполняется (2.93). Тогда результат прогонов образует выборку случайных величин 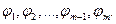Обозначим вероятность того, что 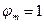, т.е. программа отказывает, как Р; а вероятность Р₀ того. что 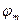принимает значение 0, а программа исправна. Тогда выбор значения

Р₀ =0,99 означает, что в серии из 100 прогонов вероятно в среднем появление одного отказа.

Применение последовательного анализа позволяет существенно ограничить число испытаний на надёжность ПО и не налагает жёстких требований на закон распределения случайной величины 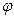. Практическое применение последовательного анализа будет продемонстрировано ниже.

Большое значение для получения приближенных оценок показателей надёжности ПО имеют так называемые метрики Холстеда. Эти же метрики позволяют численно оценить и другие характеристики ПО: длину программы, её объём, уровень программы, её интеллектуальное содержание, длительность разработки и т.п. Метрики прошли серьезную практическую апробацию и показали приемлемую для практических расчётов точность. Рассмотрим сущность метода Холстеда.

Для любой программы можно определить:

- число различных операций , например, 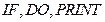и др.;

- общее число всех операндов 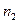(переменных и констант);

- общее число всех операций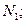

- общее число всех операндов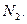

Тогда словарь программы есть 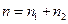, а длина реализации составляет 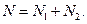Длина программы в этом случае равна

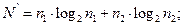(2.96)

а объём программы 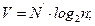(2.97)

потенциальный объём программы

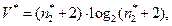(2.98)

где 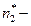минимальное число различных операндов (точнее, число независимых входных и выходных величин).

Потенциальный объём 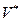- минимально возможный объём определённого алгоритма. Уровень программы L определяется через отношение потенциального объёма к объёму программы

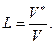(2.99)

Работа по программированию Е оценивается как суммарное число элементарных мысленных отличий между элементами, необходимых для генерации программы:

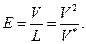(2.100)

Уровень языка позволяет оценивать преимущество языка более высокого уровня по сравнению со своим предшественником и определяется выражением

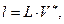(2.101)

что позволяет иначе выразить характеристики Е и V:

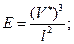(2.102)

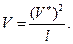(2.103)

В таблице 2.2 приведены численные значения для языков различного уровня.

 

Таблица 2.2 – Численные значения уровня языка

Язык	Уровень
Ассемблер	0,88
Бейсик	1,14
Английский	2,16

Трудоемкость разработки программного обеспечения определяется по формуле

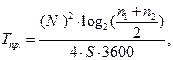чел. - часов; (2.104)

где 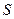- параметр Страуда, т.е. время, которое необходимо человеческому мозгу для определения существенного отличия между двумя элементами, оценивается значением 5-20 существенных различий в секунду.

Замечено, что при разработке сложных программ трудоёмкость их создания и количество выявленных при отладке ошибок существенно возрастают. При этом число переданных ошибок пропорционально объёму программы.

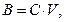(2.105)

или 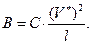(2.106)

Коэффициент пропорциональности С определяют, исходя из следующих соображений. В соответствии с эмпирическим законом Д. Миллера «7 2» для 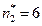определим, что 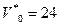, а для английского языка с учётом (2.100) получим

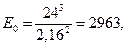
что позволяет оценить коэффициент С как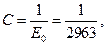

однако для языков более низкого уровня правильнее оценивать С, используя выражение более общего вида

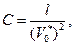(2.107)

что, в частности, для Ассемблера даёт значение 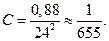Таким образом,

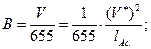(2.108)

или в более общей форме

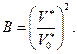(2.109)

Значения величин и 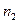могут быть определены из результатов анализа ПО или косвенно путем решения уравнений Холстеда, если известны значения 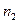и :

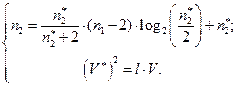(2.110)

2.3.2 Методика оценки числа оставшихся ошибок в программе

Оценка потенциального числа ошибок в ПО перед началом разработки программы может быть проведена путём расчёта количества независимых входных и выходных величин , потенциального объёма программы и возможного числа ошибок в ней. Приведём примеры анализа входных и выходных данных.

Пример 1. Рассматривается система контроля посадки самолётов в условиях ограниченной видимости. В состав системы входят курсовой радиомаяк, глиссадный радиомаяк, ответчик радиодальномера. Входными величинами системы являются: три пространственные координаты (азимут, угол места, дальность), всего количество координат равно 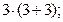Три информационных эталонных канала, т.е. - 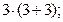четыре координаты самолёта (высота, путевая скорость, крен, тангаж).

Всего есть сорок входных величин. Выходных величин для каждого информационного канала будет четыре (три пространственные координаты плюс время), т.е. всего 12 независимых величин.

Решение.

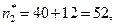
потенциальный объём программы равен

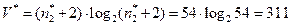бит,

а количество потенциальных ошибок в ПО равно

 

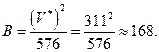
Пример 2. Определить характеристики программного обеспечения для боевой космической станции (БКС) системы противоракетной обороны (ПРО) типа стратегической оборонной инициативы президента США Рейгана. БКС должна быть рассчитана на перехват около 1000 целей с расстояния примерно 400 км.

Решение. Для перехвата необходимо рассчитать местоположение целей, их скорость, расстояние до них и условные параметры прицеливания. Упростим задачу и попытаемся получить оценку снизу. Поэтому не будем рассматривать задачи распознавания целей и согласования полученных данных с моделью боевой ситуации. Будем рассматривать предельно простой случай полной децентрализации, когда процессор управляющего компьютера непосредственно подключён к датчикам БКС и обрабатывает данные о координатах наблюдаемых объектов с целью вычислить их положение на момент перехвата. Полагаем, что на одном экране БКС появляется одновременно не более 20 целей, а 30 последовательных измерений положения объекта и его скорости статистически достаточно для получения необходимой точности и выбора наилучшего момента поражения одной цели.

Пусть для определения природы объекта необходимо измерить пять величин и на экране измеряются две координаты для каждого из 20 объектов. Таким образом, количество входных величин оказывается равным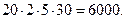

Выходные величины программы – это угловые координаты целей и расстояние до них. Для 20 целей количество выходных величин составляет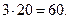

Итак,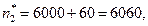

что даёт для потенциального объёма программы значение равное

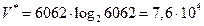бит.

Расчёты показывают, что для создания такого объёмного ПО требуется около 10¹² чел. - часов. Потенциальное количество ошибок в этом гигантском по объёму ПО для языков различного уровня равно:

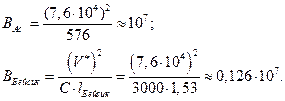
На устранение такого огромного количества ошибок может потребоваться значительно больше времени, чем на создание самого программного обеспечения. Поэтому разработка ПО такого большого объёма сомнительна.

Выполним расчёт потенциального количества ошибок в ПО перед началом комплексной отладки. Уточнение значения числа ошибок можно было бы провести путём прямого подсчёта значений и 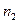. Однако для программ, написанных на языке низкого уровня это сделать затруднительно. Возможен иной подход, который рассмотрим для ПО при условиях примера 1. Особенностью этого ПО является то, что оно написано на Ассемблере.

Значение складывается из числа команд 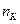, используемой системы команд и из числа отдельных подпрограмм 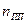. В ПО примера использовалось 45 различных операторов, число подпрограмм составило 157. Таким образом,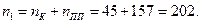

Количество операндов 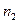равно сумме 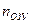(различные переменные и массивы данных, используемых в ПО); плюс количество локальных меток 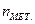и констант 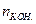. Для облегчения подсчёта 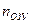используют имеющееся распределение памяти оперативного запоминающее устройства (ОЗУ), при этом подходе исключается повторяемость соответствующих операндов. Число локальных меток подсчитывают по тексту программы на Ассемблере слева от мнемонической записи команды. Таким способом гарантируется не повторяемость меток, а общепринятая табуляция облегчает подсчёт. Сложнее сосчитать число различных констант, которые оформляются в массивы числовых данных и используются при адресации в Ассемблере. Поэтому по тексту программы считают лишь число констант, заведомо помещающихся в одном байте. Как правило, они выделяются в тексте и вероятность их совпадения очень мала. К значению этой величины прибавляют 256 – число возможных байтовых констант. Для рассматриваемого ПО указанные величины имеют следующие значения:

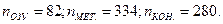
Тогда

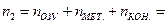82 + 334 + 280 + 256 = 952.

Полученные значения и 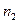можно сопоставить с расчётными значениями, которые определены из решения уравнений Холстеда для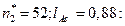

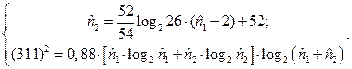
В результате решения 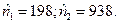Эти значения можно полагать приемлемыми (отличие от реального ПО составляет 11,0 % и 10,5 %).

Рассчитаем длину программы

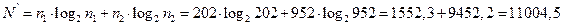
и определим объём программы

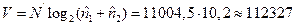бит.

Уточнённая оценка переданного количества ошибок в ПО равна:

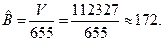
Оценка 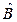отличается от полученной ранее 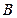= 168 лишь на 12 % и по своему смыслу является более близкой к реальности.

2.3.3 Методика расчёта интенсивности обнаружения ошибок в зависимости от времени эксплуатации программы

В процессе комплексной отладки ПО видоизменяется с целью осуществления недостающих функций и внесения исправлений для обнаруженных ошибок в уже реализованной программе. Такие изменения обычно заносятся в специальный журнал учёта исправлений с указанием даты и семантики исправления. В качестве примера рассмотрим ПО из примера 1. Исходными данными являются результаты комплексной отладки этого ПО примерно за двухлетний период. Количество обнаруженных ошибок фиксировалось помесячно, поэтому интенсивность обнаружения ошибок имеет размер «количество ошибок/месяц». Значения интенсивности обнаружения ошибок за 20 месяцев приведены ниже в таблице. Таблица 2.3 - Значения интенсивности обнаружения ошибок

Δti
r(ti)
Δti
r(ti)

 

Используя экспоненциальную аппроксимацию 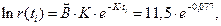что даёт значение количества оставшихся ошибок 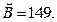Это значение хорошо согласуется с ранее определенными значениям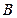и и .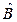

Экспоненциальная аппроксимация интенсивности обнаружения ошибок может быть использована для прогностического расчёта количества оставшихся ошибок, если определить интенсивность определения ошибок на какое-то время вперед, например, на квартал.

Таблица 2.4 - Интенсивность обнаружения ошибок на квартал вперед

Δti
r(ti)

2.3.4 Статистическая оценка вероятности безотказной работы

программного обеспечения

Рассмотрим метод последовательного анализа для оценки вероятности безотказной работы программы. В нём вводится допущение о том, что если вероятность успешного прогона Р находится в достаточно малой окрестности точки Р₀, то риск принятия неправильного решения допустимо мал. Под неправильным решением понимают решение отвергнуть надёжную программу или пропустить не надёжную программу. Для формализации этого допущения задают такие P` и P`` (P`<P₀<P``), что принятие не надёжной программы рассматривается как ошибочное решение только при 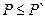, а отказ от надёжной программы является ошибочным в случае, когда 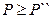. После задания значений вероятностей P` и P`` допустимый риск принятия неправильных решений таков, что вероятность ошибки первого рода, т.е. отказа от надёжной программы, не должна превышать α = Вер 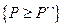, а вероятность ошибки второго рода, т.е. принятия не надёжной программы не должна превышать β = Вер 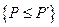. Значения величин α и β при этом назначаются, исходя из разумного компромисса, до начала испытаний, так как с их уменьшением растёт объём испытаний.

Сущность последовательного анализа гипотезы Н₀ (Р = Р₀) состоит в проверке двух конкурирующих гипотез Н`(P = P`) и H``(P = P``). Здесь под вероятностью безотказной работы ПО P(m) понимают вероятность получения выборки 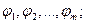в которой для 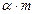элементов P`<P_m,P``, тогда

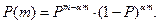(2.111)

Если верна гипотеза H`, то

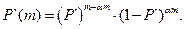(2.112)

Аналогично, если верна гипотеза H``, то

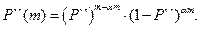(2.113)

Составим отношение «правдоподобия»:

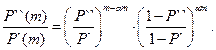(2.114)

Последовательный анализ проводится до тех пор, пока не будет выполняться следующие неравенства:

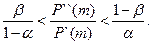(2.115)

Если на этапе m 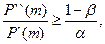то ПО не надёжно; а если 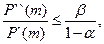то ПО можно принять как надёжное.

Прологарифмировав выражения (2.114) и (2.115), можно придать им графическую форму в координатах m, 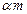. После логарифмирования и преобразований получим:

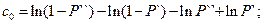
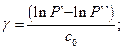
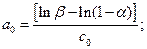
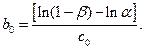
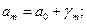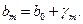Теперь можно построить две прямые и Если 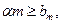то ПО не надёжно, если же 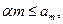то ПО можно принять как надёжное. При условии 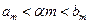испытания следует продолжать.

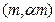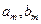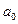На плоскости строятся прямые с одинаковым наклоном и точками пересечения оси ординат и 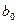соответственно.

 

Рисунок 2.12 - Примерные графические результаты

последовательного анализа

 

Итак, план действий при выполнении последовательного анализа является таковым:

- задать перед началом испытаний значения величин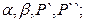

- построить прямые лини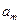и и 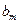, как это сделано на рис. 2.12;

- в ходе испытаний наносить на график полученные точки ();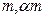

- если текущая точка 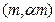попадает выше линии 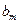, то испытания завершаются, а ПО признаётся не удовлетворяющим заданным требованиям по надёжности;

- если текущая точка 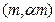попадает ниже линии 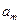, то испытания завершаются, а ПО признаётся надёжным;

- испытания продолжаются, если текущая точка 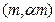находится внутри области ограниченной прямым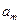и и .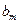

Изложенный метод удобен и прост в практической работе. Следует отметить, что метод последовательного анализа требует обеспечения независимости испытаний (прогонов) программы. Для обеспечения независимости прогонов могут быть использованы различные генераторы тестовых наборов данных. В них генерация числовых значений, выбор символических значений и значений ключевых полей осуществляется с помощью алгоритмов, выдающих совокупности случайных чисел с последующим формированием потоков входных сообщений, модельных экземпляров баз данных разнообразной структуры. Для автоматизации последовательного анализа разработаны специальные программы.

При использовании метода последовательного анализа очень важно оценить среднее число испытаний 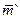при истинности гипотезы H` и среднее число испытаний 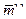при истинности гипотезы H``. В первом случае

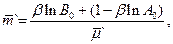(2.116)

где 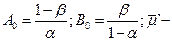математическое ожидание случайной величины 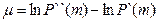при истинности гипотезы H`. Очевидно, что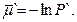

Во втором случае

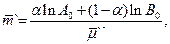(2.117)

где 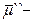математическое ожидание случайной величины при истинности гипотезы H``,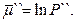

Рассмотрим примеры расчёта среднего числа испытаний.

Пример 3. Пусть 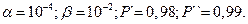Необходимо определить среднее число испытаний программы.

Решение.

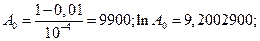
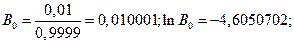
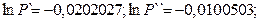
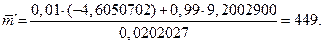
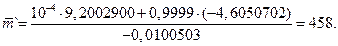
Пример 4. Пусть 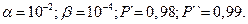Определить среднее число испытаний программного обеспечения.

Решение.

 

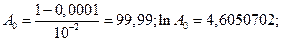
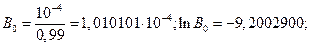
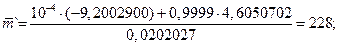
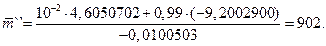
2.3.5 Рекомендации по повышению надёжности программного обеспечения

Как было показано в 2.3.1 количество оставшихся в ПО ошибок В пропорционально объёму программы V. Уменьшение числа различных операций и операндов 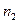, от которых зависит объём программы, приводит к снижению числа переданных ошибок. Из примеров 1 и 2 ясно, что можно рекомендовать следующие способы снижения количества переданных ошибок и повышения надёжности ПО:

1. Уменьшение общего количества локальных меток. Для этого необходимо минимизировать число условных переходов в ПО и, где возможно, отказаться от применения безусловных переходов. Эти принципы соответствуют рекомендациям структурного программирования.

2. Программируемый алгоритм должен иметь «приведённый» вид, т.е. иметь минимальное количество констант. Этому способствуют операции выделения общего множителя, приведения подобных членов в алгебраических выражениях и т.п.

3. Реализуемый алгоритм должен быть оптимальным по объёму используемого ОЗУ, т.е. по числу переменных. Этому требованию отвечает концепция использования локальных, рабочих переменных, стека.

4. Необходимо стремиться к тому, чтобы обходиться минимальным набором команд при реализации алгоритма.

5. Не следует сильно увеличивать библиотеку стандартных подпрограмм. Лучше отдать предпочтение эффективным и универсальным подпрограммам, реализующим сразу несколько операций.

Таким образом, минимизация объёма ПО при соблюдении требований спецификаций к ПО приводит к уменьшению количества ожидаемого ошибок в ПО. Основные способы повышения надёжности программного обеспечения таковы:

1) совершенствование технологии программирования;

2) выбор алгоритмов, не чувствительных к нарушениям вычислительного процесса (применение алгоритмической избыточности);

3) резервирование программ (создание структурной избыточности);

4) контроль и тестирование программ с последующей их коррекцией.

Контрольные вопросы:

1.Какая система имеет основное соединение элементов?

2.Как классифицируют методы расчёта надёжности при основном соединении элементов в системе?

3.Объясните суть метода «мажоритарного» резервирования.

4.Какие два метода структурного резервирования идентичны друг другу?

5.Перечислите способы преобразования сложных схем.

6.В каком методе резервирования используется интеграл Дюамеля?

7.Что такое «программная ошибка», «прогон программы»?