Пусть функция 
определена в некоторой окрестности точки 
.
Определение 1. Предел отношения 
при 
, если он существует, называется производной функции в точке .
Обозначение: 
, 
, 
, 
.
Таким образом,
.
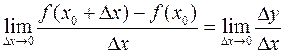(слайды 1 и 2)
Операция вычисления производной функции называется операцией дифференцирования.
Пример. Найти по определению производную функции 
в точке .
.
Пусть в прямоугольной декартовой системе координат oxy кривая Г является графиком функции (слайд 3), точки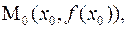 
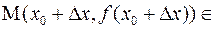Г. Прямая L, проходящая через точки М0, М, называется секущей по отношению к Г. Уравнение секущей:
.
Подставляя в уравнение секущей координаты точки М, получим
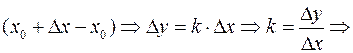
угловой коэффициент секущей есть тангенс угла 
наклона секущей к оси абсцисс.
Пусть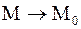 
так, что 
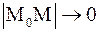. Если при этом секущая L стремится к некоторому предельному положению Т так, что угол между прямыми L и Т стремится к нулю, то прямая Т называется касательной к кривой Г в точке М0. Угловой коэффициент касательной есть тангенс угла наклона касательной в точке М0, равный пределу отношения 
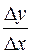при :
.
Геометрически производная функции в точке представляет собой угловой коэффициент касательной к графику функции в точке в абсциссой x0 (слайд 4).
Уравнение касательной: 
.
Переходим к вопросу о механическом смысле производной.
Пусть материальная точка движется по оси ox (слайд 5). Положение точки определяется ее абсциссой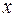 
и является функцией времени 
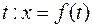. В момент времени 
материальная точка находилась в точке М0 с абсциссой . К моменту времени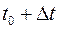 
материальная точка переместилась в точку М с абсциссой 
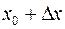. Путь, пройденный материальной точкой за время 
, составил 
. Отношение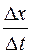 
есть средняя скорость материальной точки за время . Если существует конечный предел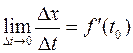 
, то он является мгновенной скоростью 
точки в момент времени . Таким образом:
.
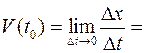
М0 
М
· ·
0 
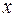
Таким образом, с механической точки зрения, если известна функция, определяющая движение объекта, то производная от этой функции в фиксированной точке равна мгновенной скорости движения в этой точке.
То же самое относится к любому процессу – физическому, химическому, биологическому, экономическому и т. д.: если известна функция, описывающая течение этого процесса, то производная от этой функции
равна скорости течения процесса (слайд 6).
Переходим к вопросу о дифференциале функции и его геометрическом смысле.
Функция называется дифференцируемой, если
D у = f ¢(х)D х + a(D х)D х,
a(D х) ® 0 при D х ® 0.
Определение 2. Дифференциалом dy функции у = f (x) в данной точке называется главная линейная часть приращения D у функции в этой точке:
dy = f ¢(x)D x.
Применение дифференциала для приближенных вычислений основано на приближенном равенстве
D у» dy Þ f (x + D х)» f (x) + f¢ (x)D х.
Геометрически, как видно из слайда 7, дифференциал функции равен той части приращения функции y = f(x), которая отсекается от этого приращения касательной, проведенной к кривой в той точке, в которой вычисляется производная и дифференциал (слайд 8).
