Методика, организация и инструментарий проведения численного эксперимента

Здесь ставится задача практически реализовать случайность внешних воздействий для разных ХТС из общего тиража. Предполагаем, что все тиражированные ХТС созданы по одной нормативной документации (технологический регламент, РД на нестандартное оборудование). Здесь же предполагается, что оборудование изготовлено на одних и тех же заводах-изготовителях, а строительные и монтажные работы проведены одним и тем же СМУ. Короче говоря, все тиражируемые ХТС - братья-близнецы. Главное, комплект внешних воздействий у них случаен и, следовательно, разный.

Процедура генерации комплекта внешних воздействий состоит в следующем. Все внешние воздействия, как это говорилось выше, объявляются взаимно-независимыми гауссовскими случайными величинами. Напоминаем, что именно они образуют поле элементарных, случайных событий. Взаимная независимость внешних воздействий, наверное, очевидна. А вот гауссовость - наша гипотеза, хотя и не принципиальная (если есть другая информация о плотности распределения вероятностей какого-то внешнего воздействия, то и ее несложно использовать).

В любом современном компьютере есть генератор случайных гауссовских величин с математическим ожиданием 0 и с дисперсией 1. Обратившись программно к генератору, получаем случайное гауссовское число Х. Далее, используем таблицу внешних воздействий на ХТС: номинальное значение каждого внешнего воздействия объявляем математическим ожиданием, а амплитуду отклонения (см. таблицу внешних воздействий) равной 3s, где s - среднее квадратическое отклонение. После этого несложно получить величину случайного внешнего воздействия:

.

Здесь буквой G обозначен, например, расход сырья в ХТС, G_НОМ - его номинальное значение, а среднеквадратическое отклонение 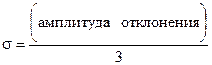. И такую процедуру проделываем столько раз, сколько всего внешних воздействий. Так формируется один комплект случайных внешних воздействий.

Далее, этот комплект направляется в программу расчета всех заданных параметров, и находятся их случайные величины (так как внешние воздействия случайны). Затем каждый найденный заданный параметр ХТС сравнивается со своим номиналом и тем самым определяется местоположение его: попал или не попал в разрешенный диапазон (см. таблицу заданных параметров). Если все заданные параметры ХТС при этом испытании (т.е. комплекте внешних воздействий) попали в свои разрешенные диапазоны, то такое сложное случайное событие называем благоприятным: ХТС работоспособна. И в соответствующую зарезервированную ячейку-сумматор добавляем 1. В противном случае (т.е. хоть один заданный параметр выскочил из разрешенного диапазона отклонения) наступает состояние отказа ХТС. Тогда в сумматор ничего не добавляется.

Если необходимо, а мы всегда это делали, то так же можно исследовать работоспособность любой части ХТС. Например, выделим подмножество заданных параметров, назначаемых химиками-технологами при разработке ХТС. Тогда при том же испытании (том же комплекте внешних воздействий) в отдельный сумматор добавлялась 1, если все заданные технологические параметры попадали в свои разрешенные диапазоны, даже если какие-то другие заданные параметры не попадали. Точно так же можно выделить заданные параметры процесщиков, машиностроителей или рассматривать их попарно, по три и т.д. Можно заняться отдельным процессом переноса или каким-то видом оборудования в составе ХТС, если у них есть заданные параметры.

При формировании второго испытания снова обращаемся к генератору случайных гауссовских величин столько раз, сколько внешних воздействий, формируя их случайную величину. Так образуется новый комплект случайных внешних воздействий, направляемых в программу расчета заданных параметров, и добавляем или не добавляем 1 в соответствующий сумматор.

И так поступаем много раз, но где же остановиться? Для нелинейных задач теория статистики не позволяет найти оптимальное число испытаний, чтобы получить “хорошую” в каком-то смысле оценку вероятности работоспособности. Тогда поступили очень просто: число испытаний определяем экспериментально. При каждом испытании рассчитывалась частота благоприятного события w: 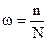, где n - число благоприятных событий (например, ХТС работоспособна), это по существу натуральное число в сумматоре, N - общее число испытаний. Далее, пользуясь специальным программным обеспечением, на мониторе ПК демонстрировался график зависимости w = w(N) (см рис.3.3.).

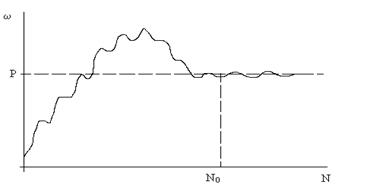
Рис. 3.3 Типичная зависимость частоты w благоприятного события от числа испытаний N. Величина Р принимается за оценку вероятности работоспособности ХТС

Чисто программно не сложно вывести на экран монитора ПК частоту благоприятных событий (т.е. работоспособность) частей ХТС. Наверное, понятно, что их частота выходила на “стационар” раньше, чем N = N₀. Таким образом, получали оценки вероятностей работоспособности частей ХТС и ее самой.

На практике для современных ХТС число испытаний N₀ выхода частоты w на стационар имело порядок 10⁵, а время счета на ПК сильно зависело от искусства вычислителя и “скорострельности” ПК.

Предупреждение. Оказывается, в практике статистических испытаний типа Монте Карло стоит проблема получения больших массивов взаимно-независимых и одинаково распределенных в вероятностном смысле случайных чисел. В одном научном коллективе (Ю.М. Быков, МИХМ, автор участвовал в работе) эту проблему решили так, что и не стали ее решать: взяли “слабенький” изотоп Со⁶⁰ и счетчик Гейгера, тогда число “щелчков” в счетчике за фиксированное время счета будет, как хорошо известно, и проверено, распределено по Пуассону. Счетчик через интерфейс соединен с ПК, а далее чисто алгоритмически несложно превратить случайную величину с распределением Пуассона в другую случайную величину с любым распределением.

Суть проблемы в том, чтобы получить достоверную оценку вероятности работоспособности, а одно из условий этого - взаимная независимость испытаний. С другой стороны, генератор случайных чисел в ПК выдает их чисто алгоритмически, т.е. реализует детерминированный механизм получения чисел, который пользователи воспринимают как бы случайным. И действительно, если построить эмпирическую функцию плотности распределения вероятностей случайных чисел от генератора в ПК, то получаем гистограмму, которая очень хорошо апроксимируется кривой Гаусса.

Но математики очень подозрительные люди и никому не верят, даже себе. Мы исследовали генератор случайных чисел в нашем ПК на предмет взаимной независимости этих чисел и на возможность существования периодики. Для этого построили корреляционную функцию случайного процесса [51] по одной очень длинной реализации (последовательности чисел от генератора). В качестве “времени” взяли номер обращения к генератору.

Рассмотрение оценки корреляционной функции показало, что любые три соседние значения случайного процесса от генератора нашего ПК “знают” друг о друге, т.е. коррелированны, а для случайных гауссовских величин это означает взаимную зависимость в вероятностном смысле. Более того, полученный случайный процесс имеет периодичность: через 6∙10⁴ обращений к генератору он, оказывается, повторяет свои характеристики.

Пришлось в общей программе численного эксперимента сделать специальную подпрограмму работы с генератором случайных чисел в ПК. Дело в том, что для получения случайной величины внешнего воздействия на ХТС пришлось теперь использовать только каждое четвертое обращение к генератору (три обращения делали “холостыми”). Кроме того, пришлось отслеживать общее число обращений к генератору, и как только это число равнялось 5∙10⁴, так чисто программно изменяли начало работы генератора, используя стандартную таблицу случайных чисел. Таким образом, при общем числе испытаний 10⁵ пришлось обращаться к генератору случайных чисел 4*10⁵ раз и раз менять начало работы генератора (конечно, все это в автоматическом режиме). Только теперь можно быть уверенным в отсутствии систематического “насилия” генератора случайных чисел в ПК на качество статистической оценки вероятности работоспособности ХТС.