1. Погрешность измерения (абсолютную, относительную) округляют, записывая ее значение:
а) двумя цифрами, если первая значащая цифра вычисленного значения погрешности 1 или 2:
Примеры: 0,00145 ≈ 0,0015 1,237% ≈ 1,3%
б) до первой значащей цифры, если первая значащая цифра 3, 4, ….9
Примеры: 8.27 ≈ 9; 0.0862% ≈ 0.09%; 0.00035 ≈ 0.0004; 43.5 ≈ 5;
2. Результаты измерения округляют с точностью «до погрешности», т.е. последняя значащая цифра в результате должна находиться в том же разряде, что и в погрешности.
3. Примеры: 243.871 ± 0.026; 243.87 ± 0.03; 243.871 ± 2.6 ≈ 244 ± 3; 1053 ± 47 ≈ 1050 ± 50.
4. Округление результата измерения достигается простым отбрасыванием цифр, если первая из отбрасываемых цифр меньше 5. Примеры: 8.337 (округлить до десятых) ≈ 8.3;
5. Если первая из отбрасываемых цифр больше или равна 5, (а за ней одна или несколько цифр отличны от нуля), то последняя из остающихся цифр увеличивается на единицу.
Примеры: 8.3351 (округлить дл сотых) ≈ 8.34; 0.2510 (округлитьь до десятых) ≈ 0.3;
При обработке результатов прямых многократных измерений предлагается следующий порядок операций:
1. Проведите n измерений и результаты каждого измерения x i запишите в таблицу.
2. Вычислите среднее значение из n измерений
 = (Σ x i)/ n.
= (Σ x i)/ n.
3. Найдите погрешность отдельного измерения
 .
.
4. Вычислите квадраты погрешностей отдельных измерений
(Δx 1)2, (Δx 2)2,..., (Δx n)2.
5. Определите среднеквадратичную погрешность среднего арифметического 

6. Задайте значение доверительной вероятности (обычно берут Pд = 0.95или 0.99).
7. Определите коэффициент Стьюдента t для заданной доверительной вероятности Pд и числа произведенных измерений n.
8. Найдите доверительный интервал (погрешность измерения) Δxд = 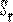 · t.
· t.
9. Окончательный результат запишите в виде  д.
д.






