

19. Бернулли схемасындағы ең ықтимал табыс саны.
Оқиғаның әр тәуелсіз тәжірибеде пайда болу ықтималдығы Р болса, онда n тәжірибеде осы оқиғаның пайда болу саны k0 ең ықтимал сан деп аталады, егер k0 саны осы тәжірибелерден пайда болуы мүмкін басқа нәтижелердің ықтималдықтарынан асып кетсе немесе кем болмаса. Енді осы ең ықтималды сан k0-ді анықтаудың жалпы формуласын табайық. Ол үшін ең үлкен ықтималдықты Рn (k0) деп ұйғарайық та, оның алдындағы Рn (k0-1) мен одан кейінгі
Рn (k0+1) ықтималдығын алайық. Сонымен
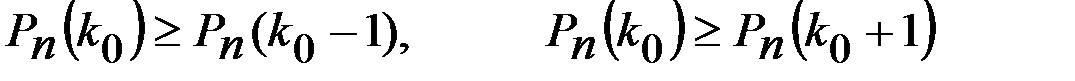
болады. Бұлардың әр қайсысын жеке жеке қарастырайық. Сонда
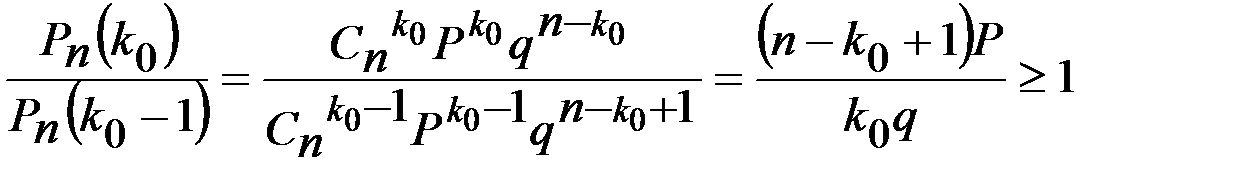
болып келеді. Бұдан К0≤np+p екені шығады. Екінші теңсіздіктен

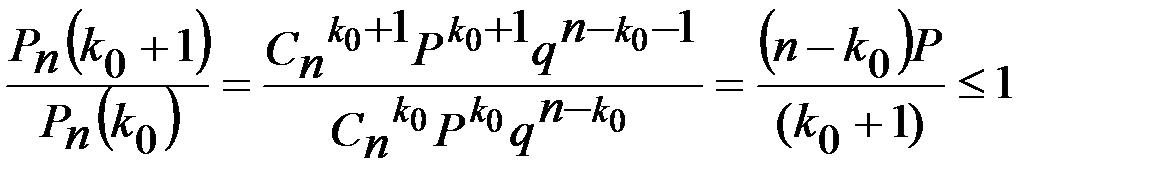 .
.
Бұдан  ≥ np-q Бұл екі теңсіздікті біріктіргенде, np-q≤
≥ np-q Бұл екі теңсіздікті біріктіргенде, np-q≤  ≤np+p болады. Бұл теңсіздіктің оң жақ бөлігін түрлендірейік:
≤np+p болады. Бұл теңсіздіктің оң жақ бөлігін түрлендірейік:
np+p=np+(1-q)=(np-q)+1.
Сонымен, алдыңғы теңсіздіктің оң жақ бөлігі сол жақ бөлігінен бір бүтін бірлікке артық. np-q мен np+p сандары бөлшек болса, онда айырымы бірге тең екі бөлшек сан шығады, бірақ m мәні бүтін сан болғандықтан, ең ықтималды сан біреу ғана болады.
Сонымен, ең ықтимал сан  қос теңсіздіктен анықталады
қос теңсіздіктен анықталады
np-q≤  ≤n+p (1) және егер:
≤n+p (1) және егер:
а) np-q бөлшек сан болса, онда бір ең ықтимал сан  болады;
болады;
б) np-q бүтін сан болса, онда екі ең ықтимал сан  және
және  +1 болады;
+1 болады;
в) np бүтін сан болса, онда ең ықтимал сан  =np болады.
=np болады.
Мысал: Тәуелсіз 6 сынау жүргізілсін дейік. Оның әрқайсысында А оқиғасының пайда болу ықтималдығы 0,2-ге тең. А оқиғасының пайда болуының ең жоғары ықтималдықты санын табу керек. Шешуі: Есептің шарты бойынша n=6; p=0,2; q=0,8. Ең ықтимал сан  -ді табу үшін (1) қос теңсіздігін пайдаланамыз. Осыған есептің берілгенін қойсақ, 6∙0,2-0,8≤
-ді табу үшін (1) қос теңсіздігін пайдаланамыз. Осыған есептің берілгенін қойсақ, 6∙0,2-0,8≤  ≤6∙0,2+0,2 немесе 0,4≤
≤6∙0,2+0,2 немесе 0,4≤  ≤1,4 болады. Мұндағы np+p=1,4, ал np-q=0,4 бөлшек сандары болғандықтан
≤1,4 болады. Мұндағы np+p=1,4, ал np-q=0,4 бөлшек сандары болғандықтан  =1.
=1.
20. Пуассонның жуықтау формуласы.

21. Муавр-Лапластың жергіліктік және интегралдық теоремалары. Қолданылу мысалдары

22. Кездейсоқ шама: анықтамасы, үлестірім заңы, үлестірім функциясы және оның қасиеттері.





24. Үзіліссіз кездейсоқ шамалар: үлестірім тығыздығы, үлестірім функциясы. Қасиеттері.

25. Екі өлшемді кездейсоқ шамалар. Олардың үлестірімі.


27. Шартты үлестірім. Қасиеттері
Егер бір аргументтің мәнін бекітіп, деп алсақ, онда шарты кезіндегі Х - Х кездейсоқ шамасының шартты үлестірімі деп аталады. Осы үлестірімнің
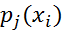 ықтималдықтары Х=хi оқиғасының шартты ықтималдықтары болады, егер Y=yj орындалды деп болжасақ. Шартты ықтималдықтың анықтамасы бойынша
ықтималдықтары Х=хi оқиғасының шартты ықтималдықтары болады, егер Y=yj орындалды деп болжасақ. Шартты ықтималдықтың анықтамасы бойынша

Тура осылай Х=хi шарты кезіндегі У кездейсоқ шамасының шартты үлестірімі шартты ықтималдықтар көмегімен беріледі:

28. Өзара тәуелсіз кездейсоқ шамалар. Тәуелсіз болу критерийлері


29. Екі өлшемді нормаль (гаустік) үлестірім.

31. Екі тәуелсіз кездейсоқ шаманың қосындысының үлестірімі. Үйірткі (свертка) формуласы.
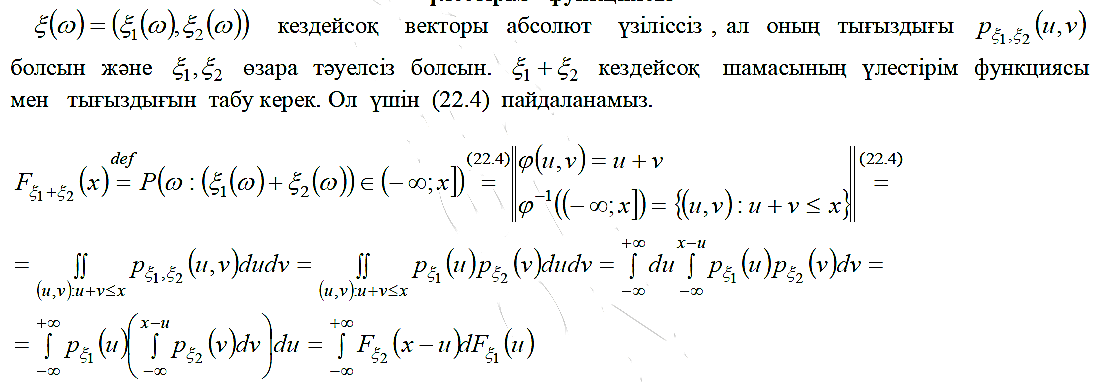
32. Нормаль үлестірілген өзара тәуелсіз кездейсоқ шамалардың қосындысының үлестірімін қорыту

Нормальді үлестірімдердің композициясы нормальді үлестірілген болады. Осылай егер Х пен У – тәуелсіз нормальді үлестірілген кездейсоқ шамалар болса, яғни, 
 болса онда кездейсоқ шамасы да нормаль үлестірілген болады
болса онда кездейсоқ шамасы да нормаль үлестірілген болады  Х пен У тәуелді болса, (корреляция коэффициенті ρ≠0), онда Z=X+Y нормальді үлестірілген болып қалады, параметрлері
Х пен У тәуелді болса, (корреляция коэффициенті ρ≠0), онда Z=X+Y нормальді үлестірілген болып қалады, параметрлері

 болады.
болады.
33. Дискретті кездейсоқ шаманың математикалық күтімі. Қасиеттері
АНЫҚТАМА. Дискреттік кездейсоқ шаманың математикалық үміті деп оның барлық мүмкін мәндерін сәйкес ықтималдықтарына көбейтіп қосқандағы қосындыны айтамыз.
Х кездейсоқ шамасының мүмкін мәндері 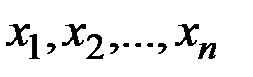 болсында олардың сәйкес ықтималдықтары
болсында олардың сәйкес ықтималдықтары 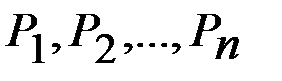 болсын. Сонда математикалық үміт мына теңдіктен анықталады:
болсын. Сонда математикалық үміт мына теңдіктен анықталады:
М(Х)=  (1)
(1)
Егер кездейсоқ шама Х-тің қабылдайтын мәндері 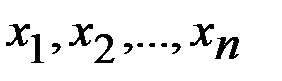 ,... ал оларға сәйкес ықтималдықтары
,... ал оларға сәйкес ықтималдықтары 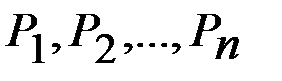 ,... болса және
,... болса және  қатары абсолютті жинақты болса, онда осы қатардың қосындысын кездейсоқ шаманың математикалық үміті дейді.
қатары абсолютті жинақты болса, онда осы қатардың қосындысын кездейсоқ шаманың математикалық үміті дейді.
М(Х)=  .
.
Енді математикалық үміттің қасиеттерін көрсетейік.
1- қасиет. Тұрақты шаманың математикалық үміті сол тұрақтының өзіне тең:
М(С)=С, С=const.
Дәлелдеу. Х-тің барлық мәндері тұрақты С-ның өзіне тең, яғни 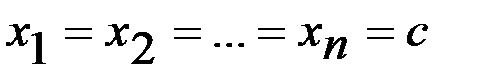 болатын кездейсоқ шама деп қарастыруымызға болады. Сонда
болатын кездейсоқ шама деп қарастыруымызға болады. Сонда
М(С)= 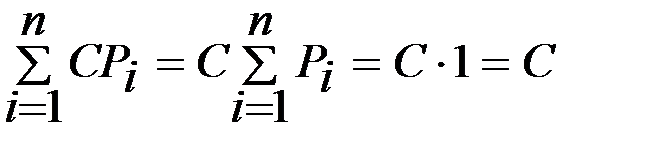 .
. 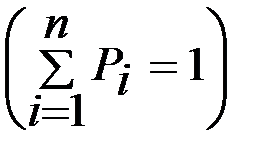
2- қасиет. Тұрақты көбейткішті математикалық үміт белгісінің сыртына шығаруға болады:
М(СХ)=СМ(Х), С=const.
Дәлелдеу. СХ-ті кездейсоқ шама деп қарастырамыз, сонда
М(СХ)= 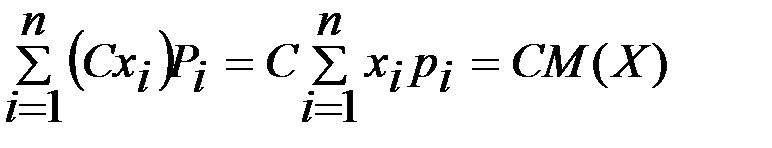 .
.
3- қасиет. Кездейсоқ екі шаманың қосындысының математикалық үміті әр кездейсоқ шамалардың математикалық үміттерінің қосындысына тең:
М(Х+У)=М(Х)+М(У).
1-салдар. Кездейсоқ 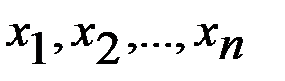 шамалардың қосындыларының математикалық үміті олардың математикалық үміттерінің қосындысына тең, яғни
шамалардың қосындыларының математикалық үміті олардың математикалық үміттерінің қосындысына тең, яғни
М 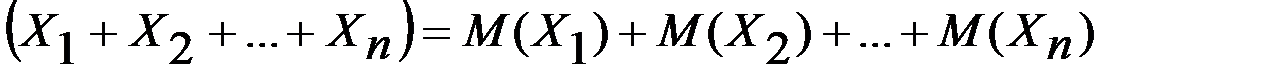 .
.
Математикалық индукция әдісімен дәлелдеу қиын емес. Бұл қасиет кездейсоқ шамалар тәуелсіз болса да, тәуелді болса да орындалады.
2-салдар. Кездейсоқ екі шаманың математикалық үміті олардың математикалық үміттерінің айырмасына тең:
М(Х-У)=М(Х)-М(У).
Дәлелдеу. (-У)-ті (-1)У деп жазып, 2 және 3 - қасиеттерді пайдаланып дәлелденеді.
3-салдар. Кездейсоқ шама мен тұрақты шама қосындысының (айырымының) математикалық үміті сол кездейсоқ шаманың математикалық үміті мен сол тұрақтының қосындысына (айырымына) тең, яғни
М 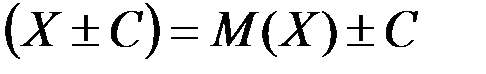 .
.
4- қасиет. Тәуелсіз екі кездейсоқ шама көбейтіндісінің математикалық үміті олардың математикалық үміттерінің көбейтіндісіне тең, яғни
M  .
.
1 -салдар. 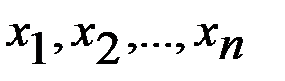 кездейсоқ шамаларды қос- қостан тәуелсіз болса, онда
кездейсоқ шамаларды қос- қостан тәуелсіз болса, онда
М 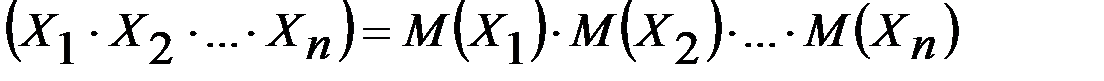 .
.
Математикалық индукция әдісімен дәлелдеу қиынға соқпайды.

Мысал. Үлестіру заңы белгілі (Х) кездейсоқ шаманың математикалық үмітін табайық:
| х | ||||
| р | 0,3 | 0,1 | 0,2 | 0,4 |
Шешуі. 
Мысал. Х және У екі тәуелсіз кездейсоқ шама үлестіру заңдарымен берілген. М(Х), М(У) кездейсоқ шамаларының математикалық үмітін табайық:
Шешуі. М(Х)=- 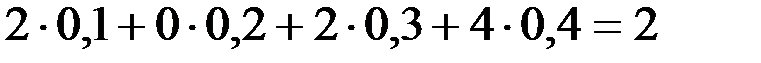 ,
,
М(У)=  .
.
Теорема-1. Егер А оқиғасының бір тәжірибедегі ықтималдығы р- ға тең болса, бір тәжірибедегі А оқиғасының пайда болу санының математикалық үміті де р-ға тең болады, яғни М(Х)=р.
| х | ||
| р | р | 1-р |
Дәлелдеу. Шынында да, А оқиғасының бір тәжірибедегі пайда болу санын кездейсоқ шама ретінде қарастырсақ, оның үлестіру заңы мынадай болады: М(Х)=  Теорема-2. n тәуелсіз тәжірибедегі А оқиғасының пайда болуы сандарының математикалық үміті тәуелсіз тәжірибелер саны мен оқиғаның әрбір тәжірибедегі пайда болуының ықтималдығы р-ның көбейтіндісіне тең: М(Х)=nр.
Теорема-2. n тәуелсіз тәжірибедегі А оқиғасының пайда болуы сандарының математикалық үміті тәуелсіз тәжірибелер саны мен оқиғаның әрбір тәжірибедегі пайда болуының ықтималдығы р-ның көбейтіндісіне тең: М(Х)=nр.
34. Дискретті кездейсоқ шаманың дисперсиясы, орта квадраттық ауытқуы. Қасиеттері
Кездейсоқ шаманың мәндері оның математикалық үмітінен ауытқитындығы түсінікті. Міне, осы ауытқуды бағалау үшін дисперсия ұғымы енгізіледі. Х кездейсоқ шаманың дисперсиясын таңбасымен D(Х) белгіленеді:
Х-дискретті кездейсоқ шама, М(Х)-осы кездейсоқ шаманың математикалық үміті болсын. Бұл жағдайда Х-М(Х) айырмасын, кездейсоқ шама мәндерінің математикалық үміттен ауытқуы деп аталады. Кездейсоқ Х шамасының таралу заңы:
| Х | 
| 
| ... | 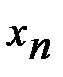
| |
| Р | 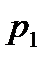
| 
| ... | 
| 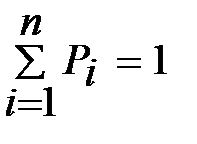
|
берілсін. Бұл жағдайда Х-М(Х) ауытқудың үлестірім заңы
| Х-М(Х) | 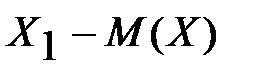
| 
| ... | 
| |
| Р | 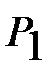
| 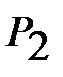
| ... | 
| 
|
Теорема. Ауытқудың математикалық үміті нөлге тең, яғни М 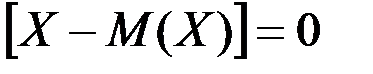 . Дәлелдеу.
. Дәлелдеу. 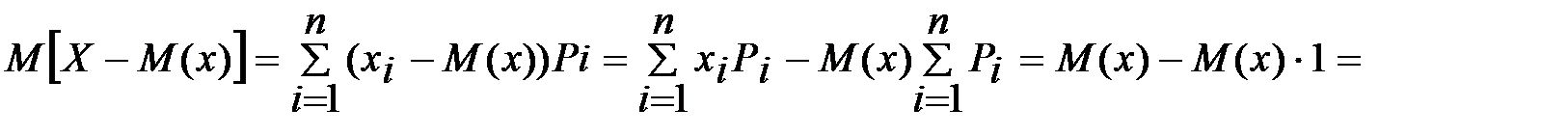
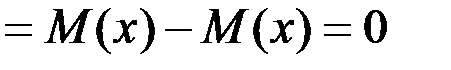 .
.
АНЫҚТАМА. Дискреттік Х кездейсоқ шамасының дисперсиясы деп кездейсоқ шаманың оның математикалық үмітінен ауытқуы квадратының математикалық үмітін айтады және оны былай белгілейді:
 .
.
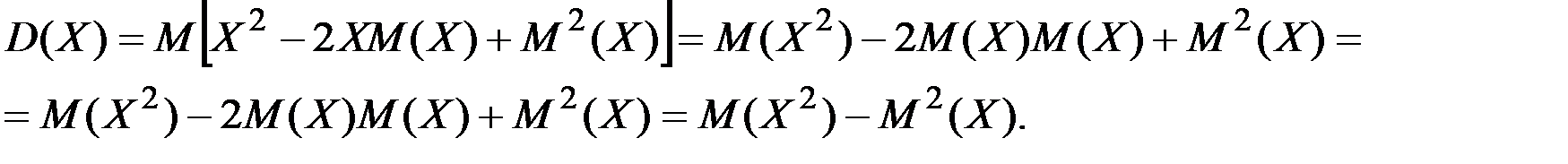
Сонымен дисперсияны анықтайтын  (2)
(2)
формуласы келіп шығады. Дисперсияның қасиеттері:
1-қасиет. Тұрақты шаманың дисперсиясы нөлге тең: D(С)=0, С=const.
Дәлелдеу. (2) формула бойынша D(С)=М(С 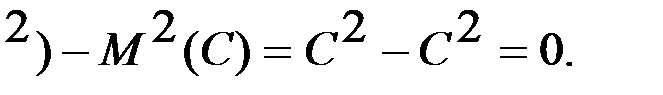
2-қасиет. Тұрақты көбейткіш дисперсия белгісінің алдына квадратталып шығады: D(СХ)=С 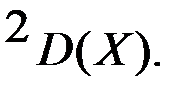
Дәлелдеу. Бұл қасиетті дәлелдеу үшін де (1) формуланы пайдаланамыз:
D(СХ)=М((СХ) 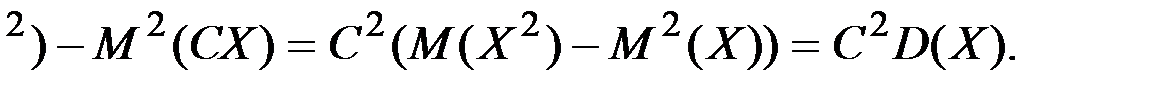
3-қасиет. Тәуелсіз екі кездейсоқ шамалардың қосындысының дисперсиясы олардың дисперсияларының қосындысына тең: (Х+У)=D(Х)+D(У).
Дәлелдеу. (1) формулаға математикалық үміттің қасиеттерін қолданып, кездейсоқ шамалардың тәуелсіздігін ескерсек,  Кездейсоқ шаманың алатын мәндерінің оның орта мәнінен ауытқуын (шашырауын) бағалау үшін тағы бір сандық сипаттама орташа квадраттық ауытқу қолданылады
Кездейсоқ шаманың алатын мәндерінің оның орта мәнінен ауытқуын (шашырауын) бағалау үшін тағы бір сандық сипаттама орташа квадраттық ауытқу қолданылады 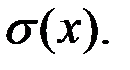
Орташа квадраттық ауытқу деп дисперсиядан алынған квадрат түбірді айтады, яғни 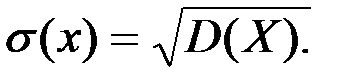 (3)
(3)
1- теорема. Егер тәжірибені бір рет жүргізгендегі А оқиғасының ықтималдығы р-ға тең болса q=1-p, ол оқиғаның пайда болу санының дисперсиясы pq-ға тең болады.
х 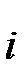
| ||
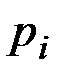
| P | q |
Дәлелдеу. Бұл жағдайда кездейсоқ шаманың үлестірілу заңын былай жазуға болады:
Дисперсияны есептеп табайық:
М(Х)= 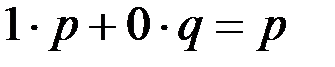 ; М(Х
; М(Х 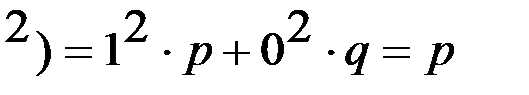 ,
,
D(Х)=М(Х 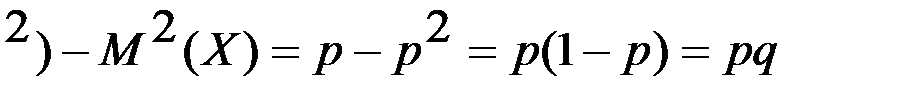 .
.
2-теорема. Егер бір тәжірибеде оқиғаның ықтималдығы р-ға тең болса q=1-p, ол оқиғаның тәжірибені n рет қайталағанда пайда болу санының дисперсиясы npq-ға тең болады, яғни D(Х)=npq.
Дәлелдеу. 1-теорема бойынша бір тәжірибеде оқиғаның пайда болу санының дисперсиясы pq-ға тең. Тәжірибе n рет қайталанғандықтан, 3- қасиет бойынша pq+pq+…+pq=npq.
Мысал. Әрбіреуінде оқиғаның пайда болу ықтималы 0,3 болатын 15 тәуелсіз тәжірибе жүргізілген. Осы тәжірибедегі оқиғаның пайда болу саны –Х шамасының дисперсиясын табу керек. Шешуі. Есептің шарты бойынша n=15, p=0,3 олай болса q=1-0,3=0,7.
Сондықтан, іздеп отырған дисперсиямыз: D(Х)= 
35. Үзіліссіз кездейсоқ шаманың математикалық күтімі. Қасиеттері.


36. Үзіліссіз кездейсоқ шаманың дисперсиясы, орта квадраттық ауытқуы. Қасиеттері
Х дискретті кездейсоқ шама болса, дисперсия
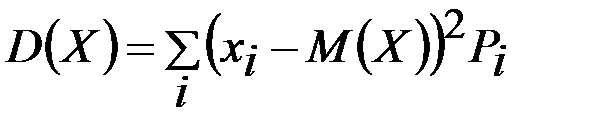
формуласымен өрнектеледі. Х – үздіксіз болса, онда дисперсия
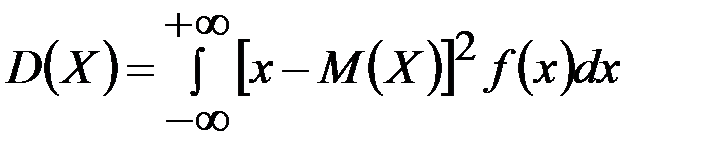
формуласымен өрнектеледі. Ал, егер де Х – тің мүмкін мәндері
[a, b] аралығында болса, онда
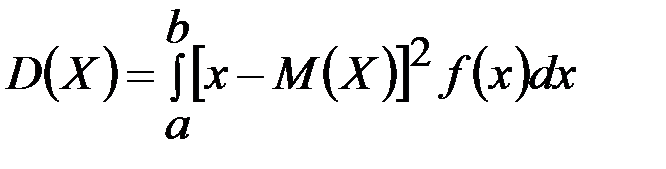
болады. Үздіксіз кездейсоқ шаманың дисперсиясын
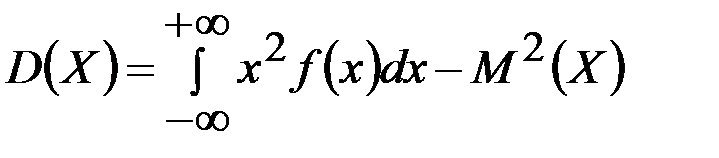
формуласы бойынша есептеген қолайлы.
Үздіксіз кездейсоқ шаманың орта квадраттық ауытқуы деп дисперсияның квадрат түбірін айтады:
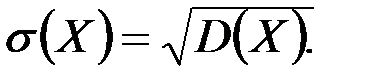
37. Биномиаль үлестірім. Анықтамасы және сандық сипаттамалары.
АНЫКТАМА: Егер Х кездейсок шамасы 0,1,2,...n мәндерін кабылдау ықтималдығы  , мундағы
, мундағы 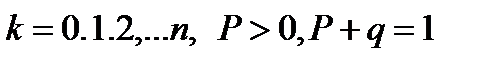
ал 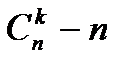 элементтен К-дан жасалган теру саны болса, онда Х-ді Бернулли заны бойынша улескен деп айтады. Немесе бұл улестірімді биномдык деп те айтады. Бернулли заны бойынша улестірілген кездейсок шаманын математикалык үмітін табалык n – рет Бернулли тәжірибесін жургізгенде А оқиғасынын пайда болу санын Х аркылы белгіледік. Жанадан кездейсок шамалар өнгізейік.
элементтен К-дан жасалган теру саны болса, онда Х-ді Бернулли заны бойынша улескен деп айтады. Немесе бұл улестірімді биномдык деп те айтады. Бернулли заны бойынша улестірілген кездейсок шаманын математикалык үмітін табалык n – рет Бернулли тәжірибесін жургізгенде А оқиғасынын пайда болу санын Х аркылы белгіледік. Жанадан кездейсок шамалар өнгізейік.
| – ші тәжиребеде пайда болса – ші тәжиребеде пайда болмаса |
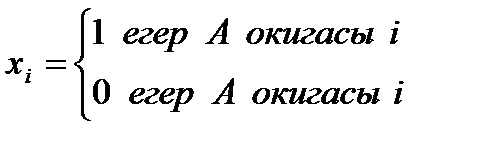
Сонда Х кездейсок шамасын  косындысы турінде жазуға болады, өйткені бүл косынды да турган әрбір косылныш не 0-ге, не 1-ге тен және бірлердін саны А оқиғасынын пайда болу саны канша болса сонша. Математикалык үміттін аныктамасын және онын касиеттері аркылы Х-дін математикалык үмітін есептеуге болады:
косындысы турінде жазуға болады, өйткені бүл косынды да турган әрбір косылныш не 0-ге, не 1-ге тен және бірлердін саны А оқиғасынын пайда болу саны канша болса сонша. Математикалык үміттін аныктамасын және онын касиеттері аркылы Х-дін математикалык үмітін есептеуге болады:
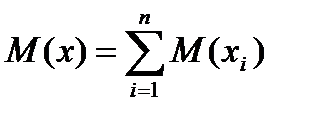
Енді хi – нын үмітін табалык: 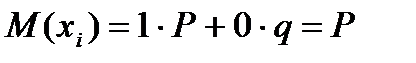
Сонымен
(13)

38. Пуассон үлестірім. Анықтамасы және сандық сипаттамалары.
АНЫКТАМА: Егер Х кездейcок шамасы 0,1,2,…n мәндерін кабылдаса және бұл мәндері кабылдау ықтималдығы:
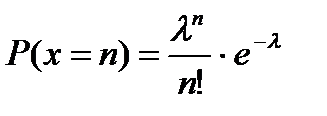
мундағы  болса, онда Х-ті Пуассон заны бойынша улескен деп айтады.
болса, онда Х-ті Пуассон заны бойынша улескен деп айтады.
Пуассон заны бойынша улестірілген Х кездейсок шамасы ушін:
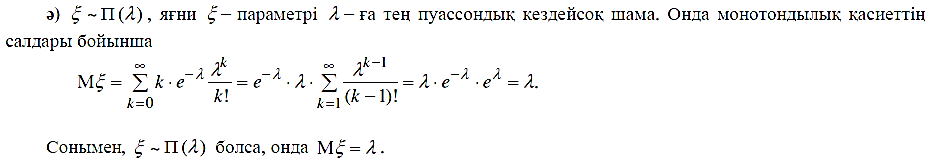
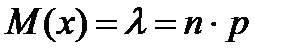 (16)
(16)
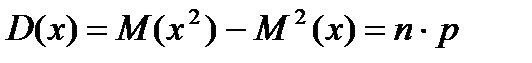 (17)
(17)
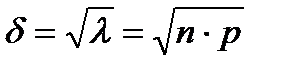 (18)
(18)
Мұндағы  Пуассон заңының параметрі деп аталады.
Пуассон заңының параметрі деп аталады.






40. Теріс биномиальді үлестірім. Анықтамасы және сандық сипаттамалары
(n,p) параметрмен үлестірілген кездейсоқ ξ шамасы теріс биномиалды үлестірілген болады, егер 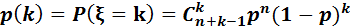
Үлестірім функциясы: 
Бернуллидің тәуелсіз сынақтар тізбегінде n-ші табыс n+k-ші сынақта пайда болуының ықтималдығын табайық. (“табыс” ықтималдығы р).
Егер n-ші табыс n+k-ші сынақта пайда болса, онда ең соңғы n+k-ші сынақта “табыс” (А оқиғасы), ал одан бұрынғы n+k-1 сынақта n-1 рет “табыс ”, k рет “сәтсіздік” болды(В оқиғасы) деген сөз. Сынақтар тәуелсіз болғандықтан іздеп отырған ықтималдығымыз мына формуламен анықталады. (k=0,1,2,….):
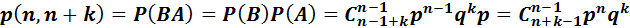 (1)
(1)
(1)-үлестірім теріс биномиальды үлестірім деп аталады. Бұл үлестірімнің атауы мына теңдікке байланысты шыққан:
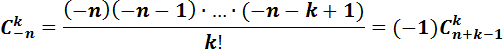
Соңғы теңдік (1)-үлестірімді басқаша жазуға мүмкіндік береді:
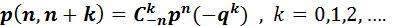 (1’)
(1’)
Мына анализден белгілі формуланы

Пайдаланып былай жаза аламыз:
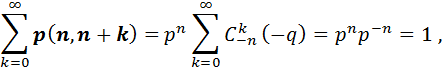
Яғни {  } шындығында да үлестірім болады. Теріс биномиалды үлестірімді кейде Паскаль үлестірімі деп те атайды.
} шындығында да үлестірім болады. Теріс биномиалды үлестірімді кейде Паскаль үлестірімі деп те атайды.
Ал n=1 болған кезде (1)-үлестірім геометриялық үлестірім деп аталады:

Теріс биномиалды үлестірімнің математикалық күтімі: 
Теріс биномиалды үлестірімнің дисперсиясы:  . Мұндағы, q=1- p.
. Мұндағы, q=1- p.
Демек, n-ші "табысқа " дейінгі толық сынақтардың санның математикалық күтiмi мынаған тең: 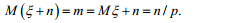
41. Гипергеометриялық үлестірім және оның сандық сипаттамалары.
Дискретті ξ кездейсоқ шамасының гипергеометриялық үлестірімі болады, егер оның k=1,2,3,....,min(n;M) мәнінде
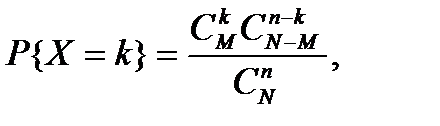
ықтималдықтары бар болса, мұндағы k=1,2,3,....,min(n;M), k≤N;n≤N;n,M,N – натурал сандар.
Алдыңғы формуладан (  ) мынандай қатынас шығатынын атай кетелік:
) мынандай қатынас шығатынын атай кетелік:
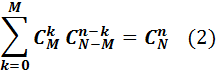
Гипергеометриялық үлестірімнің математикалық күтімін табайық:
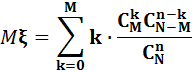
Қосынды ішіндегі 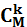 –ды
–ды  түрінде жазып, сәйкес қысқартуларды орындасақ, мынаны аламыз:
түрінде жазып, сәйкес қысқартуларды орындасақ, мынаны аламыз:
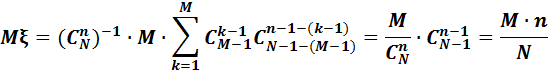
Біз жоғарыда ортаңғы қосындыны (2)-формула арқылы  түрінде жаздық. Енді
түрінде жаздық. Енді 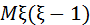 есептелік:
есептелік:
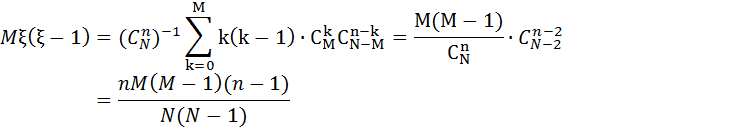
Бұдан

Теорема. n,M,N параметрімен үлестірілген ξ кездейсоқ шамасының гипергеометриялық үлестірімінің математикалық күтімі: 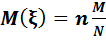
Ал дисперсиясы:  тең.
тең.
42. Бірқалыпты үлестірім. Анықтамасы және сандық сипаттамалары.
Ықтималдықтар тығыздығы

теңдiгiмен анықталатын Х кездейсоқ шамасын бiрқалыпты үлестiрiмдi (равномерное распределение) деп атайды. Енді f(x) бойынша интегралдық функция Ғ(х) мәнін анықтайық. Ол үшін 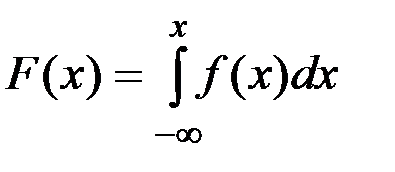 формуласын пайдаланамыз.
формуласын пайдаланамыз.
Егер х 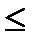 a болса, онда f(x) = 0 болды.Сондықтан Ғ(х) = 0. Егер а<x
a болса, онда f(x) = 0 болды.Сондықтан Ғ(х) = 0. Егер а<x 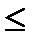 b болғанда
b болғанда
 .
.
 болғанда
болғанда
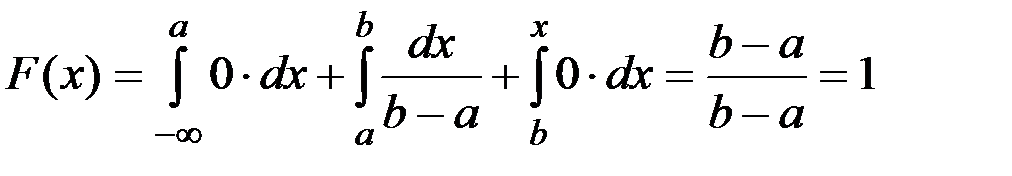 .
.
Демек,
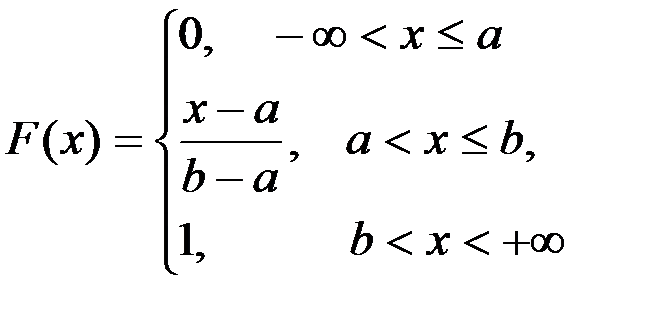
Енді математикалық үмітті және дисперцияны табайық:
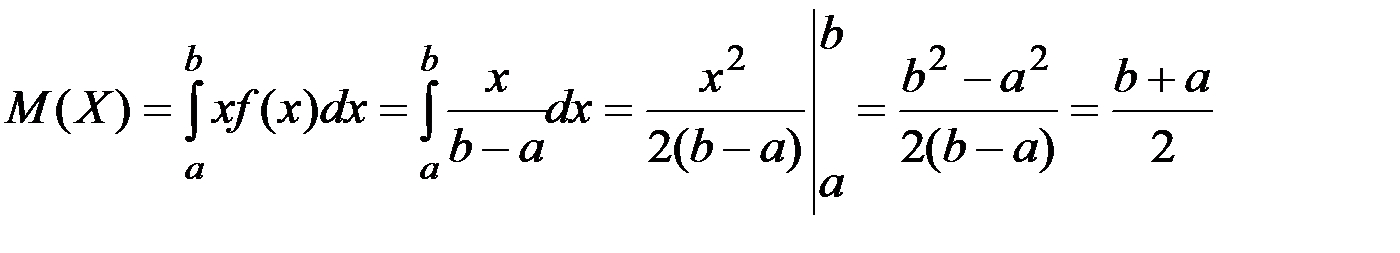 .
.

Демек, 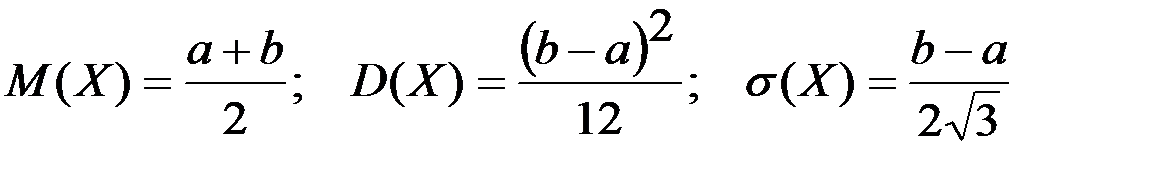
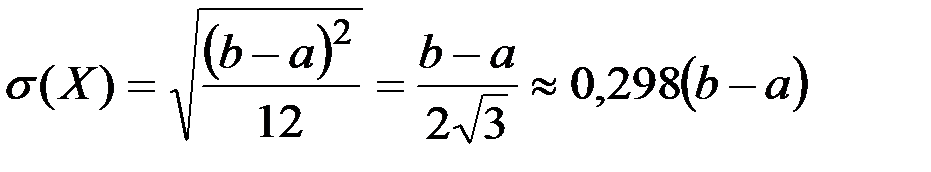 .
.
43. Көрсеткішті үлестірім. Анықтамасы және сандық сипаттамалары.
Ықтималдық тығыздығы
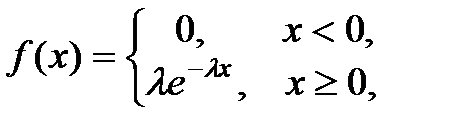
мұндағы 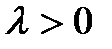 параметр, теңдiгiмен анықталатын Х кездейсоқ шамасын көрсеткiштiк заң бойынша үлестiрiмдi деп атайды. Анықтама. Егер Х кездейсоқ шамасы мына үлестірім тығыздығы
параметр, теңдiгiмен анықталатын Х кездейсоқ шамасын көрсеткiштiк заң бойынша үлестiрiмдi деп атайды. Анықтама. Егер Х кездейсоқ шамасы мына үлестірім тығыздығы
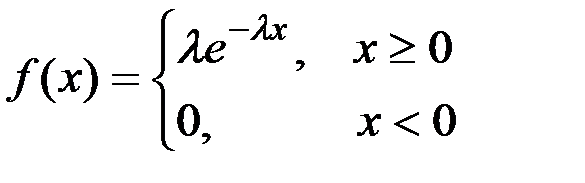
арқылы берілсе, онда ол көрсеткіштік үлестірім заңымен берілген дейді. Мұндағы 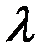 - тұрақты оң шама.
- тұрақты оң шама.
Интегралдық функциясын табайық:
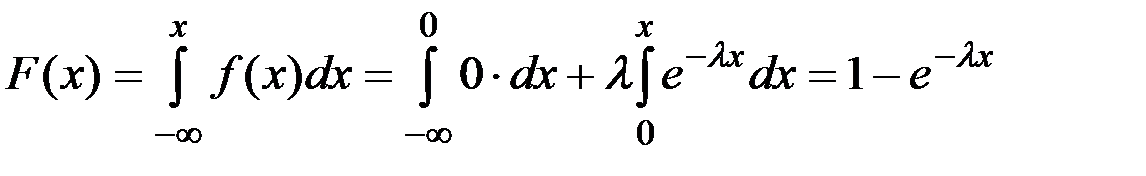 .
.
Сонымен 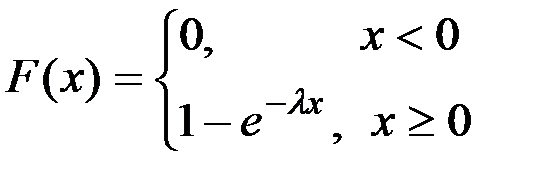
Бұл үлестірімнің сандық сипаттамалары:
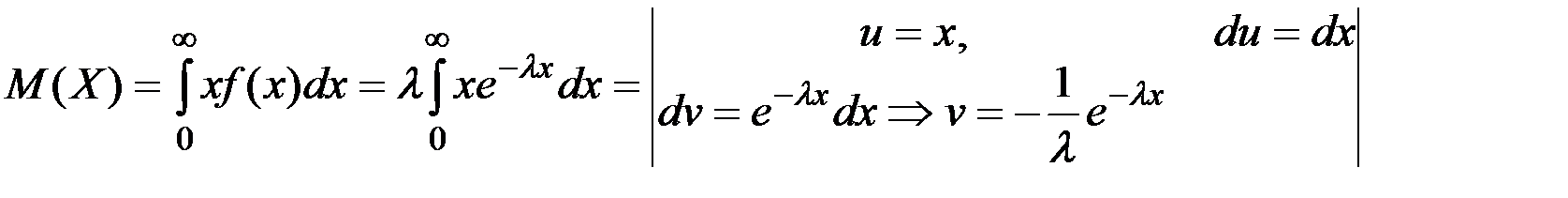
= 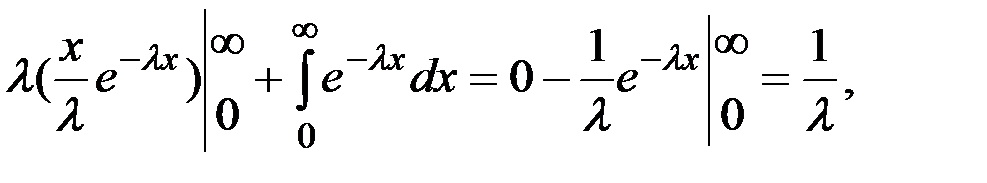 яғни
яғни 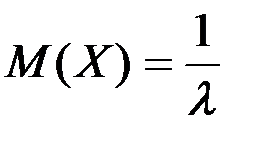 .
.
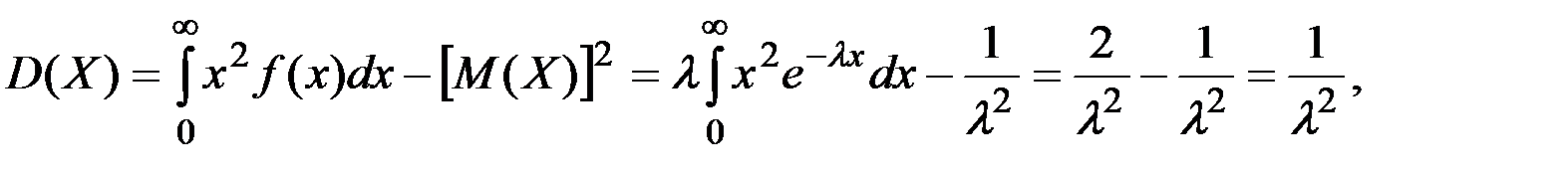
яғни 
Кездейсоқ шаманың (а; b) аралығынан мән қабылдау ықтималдығы
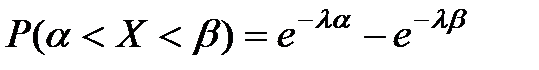 ;
;
44. Гамма үлестірім. Анықтамасы және сандық сипаттамалары.
Гамма үлестірім. Математикалық талдау курсында меншіксіз және параметрлі интегралдар тобына жататын гамма функциясының анықтамасын еске түсірелік:
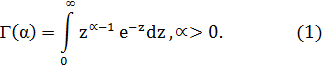
Сөйтіп,  параметрінің
параметрінің 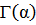 функциясы
функциясы 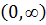 аралығында анықталған, үздіксіз.Бұл функцияны есептеу
аралығында анықталған, үздіксіз.Бұл функцияны есептеу
 формуласына негізделген.
формуласына негізделген.
(2)-формуласын дәлелдеу үшін бөліктеп интегралдаса болғаны:
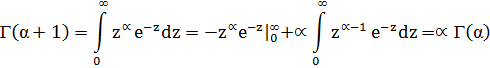
Егер n натурал сан болса, 
Гамма үлестірімді ξ кездейсоқ шамасының тығыздық функциясы
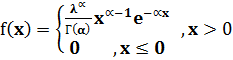 (3)
(3)
Теңдіктерімен анықталады, мұндағы α>0 және λ>0, өйткені f(x)≥0 және 
Гамма үлестірімнің сипаттауыш функциясы
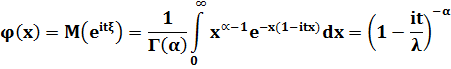
Формуласымен,ал k-шы ретті моменті
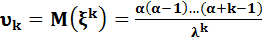 формуласымен есептеледі.
формуласымен есептеледі.
Олай болса, математикалық күтімі мен дисперсиясы табылды:
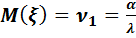 және
және 
Гамма үлестірімі арқылы бірқатар үлестірім заңдарын шығарып алуға болады.Мәселен, 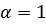 болса,гамма үлестірімі,көрсеткіштік үлестірімге айналады.
болса,гамма үлестірімі,көрсеткіштік үлестірімге айналады.
45. Нормаль үлестірім. Анықтамасы және сандық сипаттамалары.
Үздіксіз кездейсоқ Х шамасының ықтималдықтар үлестірімін қалыпты деп атайды, егер оның ықтималдықтар үлестірім заңы ықтималдық тығыздығымен анықталса
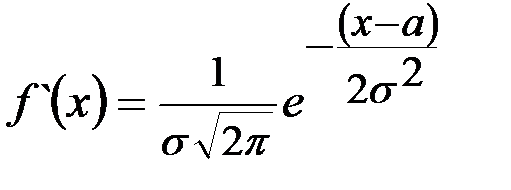 . (1)
. (1)
мұндағы  нақты параметрлер Бұл кездейсоқ шаманың математикалық үмітін табайық:
нақты параметрлер Бұл кездейсоқ шаманың математикалық үмітін табайық:


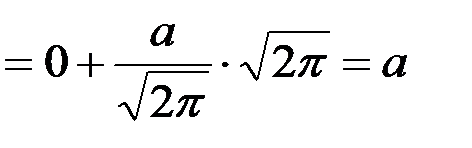 ,
,
яғни 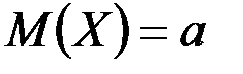 .Сонымен параметр
.Сонымен параметр 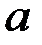 қалыпты заң үшін математикалық үміт болады.Енді дисперсиясын табайық:
қалыпты заң үшін математикалық үміт болады.Енді дисперсиясын табайық:
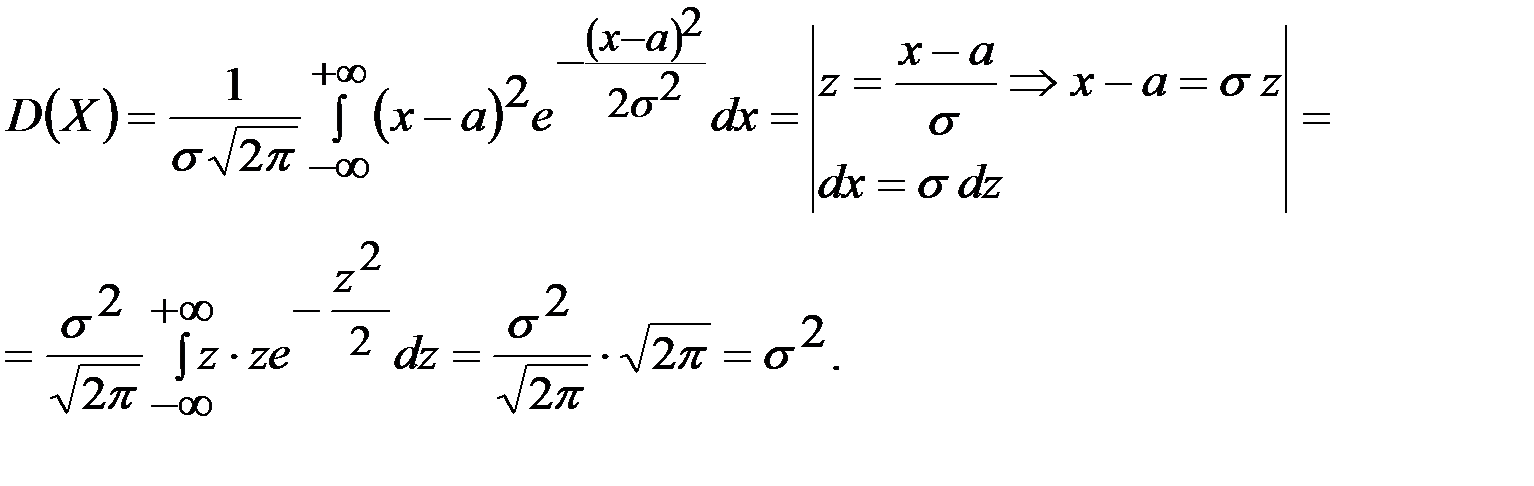
Өйткені мүшелеп интегралдасақ

болады. Сонымен, 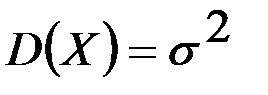 , ал
, ал 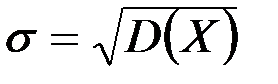 орташа квадраттық ауытқуы болады.Қалыпты үлестірімі бар кездейсоқ шаманың математикалық үміті мен дисперсиясын есептеп отырып, оның анықтамасына қатынасатын параметрлердің ықтималдық мәнін аштық: бұл анықтамадағы
орташа квадраттық ауытқуы болады.Қалыпты үлестірімі бар кездейсоқ шаманың математикалық үміті мен дисперсиясын есептеп отырып, оның анықтамасына қатынасатын параметрлердің ықтималдық мәнін аштық: бұл анықтамадағы 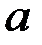 параметрі математикалық үмітті, ал
параметрі математикалық үмітті, ал  параметрі дисперсияны көрсетеді.
параметрі дисперсияны көрсетеді.
Теорема. Қалыпты үлестірімді кездейсоқ шаманың берілген 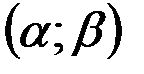 аралығына түсу ықтималдығы
аралығына түсу ықтималдығы 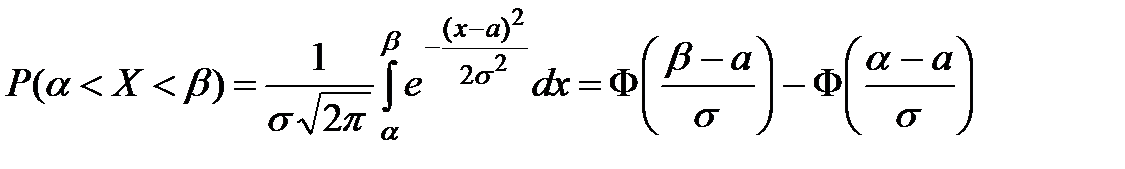 .формуласы бойынша анықталады, мұндағы
.формуласы бойынша анықталады, мұндағы 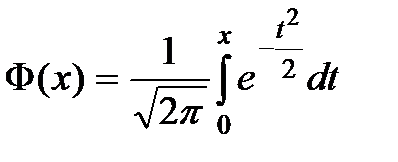 Лаплас функциясы.
Лаплас функциясы.
46.Ковариация. Ковариациялық матрица. Қасиеттері.

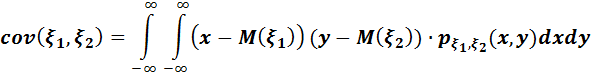
Коварияцияның 4 қасиетінің дәлелдеуі:
Егер 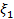 және
және  тәуелсәз кездейсоқ шамалар болса, онда
тәуелсәз кездейсоқ шамалар болса, онда

Шындығында да бұл жағдайда
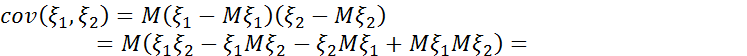
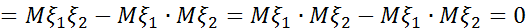
Сонымен, тәуелсіз  ,
,  кездейсоқ шамалары үшін
кездейсоқ шамалары үшін  болады.
болады.
 кездейсоқ шамалары берілсе, онда коварияциялық матрица келесі түрде болады:
кездейсоқ шамалары берілсе, онда коварияциялық матрица келесі түрде болады:
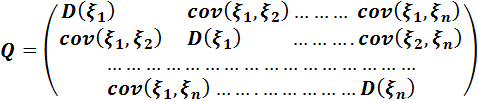
47. Корреляция коэффициенті. Қасиеттері. Корреляциялық матрица.

Теорема.1.Егер 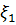 ,
, 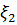 тәуелсіз кездейсоқ шамалар болса, онда олардың корреляция коэффиценті нөлге тең:
тәуелсіз кездейсоқ шамалар болса, онда олардың корреляция коэффиценті нөлге тең: 
2.Әруақытта 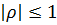 ;
;
3. 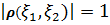 сонда тек сонда ғана,егер қандай да бір а≠0,b-тұрақтылары табылса және
сонда тек сонда ғана,егер қандай да бір а≠0,b-тұрақтылары табылса және 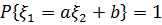 болса;
болса;
Егер ρ>0 болса 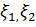 кездейсоқ шамалары оң корреляцияланған,ал ρ<0 болса теріс корреляцияланған кездейсоқ шамалар деп аталады.
кездейсоқ шамалары оң корреляцияланған,ал ρ<0 болса теріс корреляцияланған кездейсоқ шамалар деп аталады.
Корреляциялық матрица деп, қаралатын кездейсоқ шамалардың корреляция жұбының коэффициенттерi болып табылатын матрицаны қарастырамыз. Корреляциялық матрица симметриялы және оның бас диагоналында әрқашанда бір тұрады.
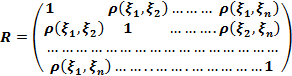
Сонымен, 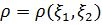 корреляция коэффиценті берілген
корреляция коэффиценті берілген 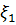 және
және 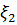 кездейсоқ шамаларының тәуелдәләк өлшемі ретінде қарастыруға болады екен: егер олар тәуелсіз болса, онда ρ=0;егер ρ=±1 болса, онда кездейсоқ шамалар бір біріне сызықты тәуелді және де ρ=1 болса
кездейсоқ шамаларының тәуелдәләк өлшемі ретінде қарастыруға болады екен: егер олар тәуелсіз болса, онда ρ=0;егер ρ=±1 болса, онда кездейсоқ шамалар бір біріне сызықты тәуелді және де ρ=1 болса 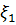
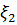 -мен бірге монотонды өседі,ρ=-1 болса
-мен бірге монотонды өседі,ρ=-1 болса 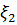
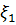 -мен бірге монотонды кемиді.
-мен бірге монотонды кемиді.
48. Гаустік кездейсоқ вектор және оның қасиеттері.
Теорема: 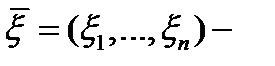 Гаустік кездейсоқ вектор. Онда оның келесі тұжырымдары болады:
Гаустік кездейсоқ вектор. Онда оның келесі тұжырымдары болады:
1)  - тәуелсіз кездейсоқ шамалар,
- тәуелсіз кездейсоқ шамалар,
2) 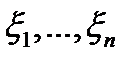 - корреляцияланбаған кездейсоқ шамалар (cov=0),
- корреляцияланбаған кездейсоқ шамалар (cov=0),
3) 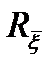 - диагональды.
- диагональды.
Ескету: 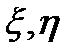 - нормальды үлестірілген кездейсоқ шамалар болса, онда
- нормальды үлестірілген кездейсоқ шамалар болса, онда 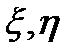 - тәуелсіз
- тәуелсіз 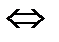
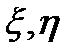 - корреляцияланбаған.
- корреляцияланбаған.
Дәлелдеу. Келесі арақатынастар айқын болады: 1)  2)
2)  3)
3)
3) 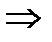 1) шығатынын көрсетейік.
1) шығатынын көрсетейік.
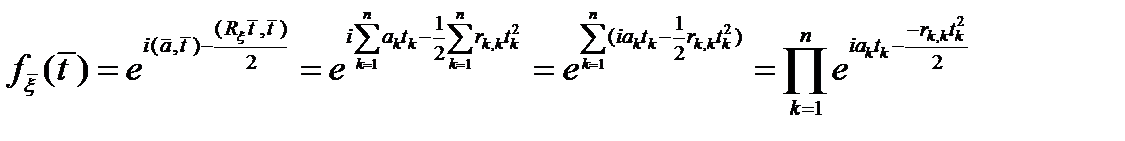 ={
={ 
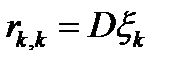 } =
} = 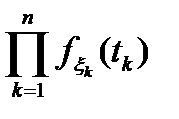
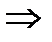
 - тәуелсіз.
- тәуелсіз.
Теорема: 1) 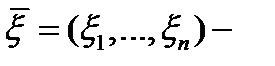
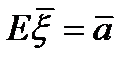 ,
, 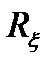 ковариациялық матрицасы және
ковариациялық матрицасы және 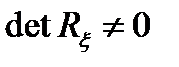 бар гаустік кездейсоқ вектор. Онда кездейсоқ вектордың
бар гаустік кездейсоқ вектор. Онда кездейсоқ вектордың 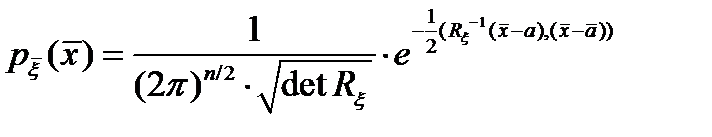 .
.
тығыздығы болады.
2) Кез келген 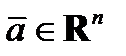 және кез келген
және кез келген  -(
-( )үшін
)үшін  кездейсоқ гаустік вектор болады және онда
кездейсоқ гаустік вектор болады және онда 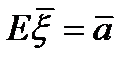 және
және 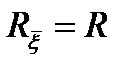 .
.
49. Чебышев теңсіздігі. Дәлелдеу.
Теорема. Егер ξ кездейсоқ шамасының дисперсиясы D(ξ) бар болса, онда кез келген ε>0 саны үшін
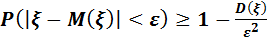 (1) -теңсіздігі орындалады.
(1) -теңсіздігі орындалады.
Чебышев теңсіздігі  айырымының абсолют шамасын ықтималдық тұрғыдан бағалауға мүмкіндік береді.
айырымының абсолют шамасын ықтималдық тұрғыдан бағалауға мүмкіндік береді.
(1)-теңсіздік
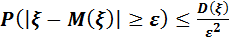 (2) - теңсіздігімен парапар, өйткені
(2) - теңсіздігімен парапар, өйткені
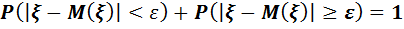
Дәлелдеу. ξ шамасының тығыздық функциясын f(x) арқылы белгілесек:
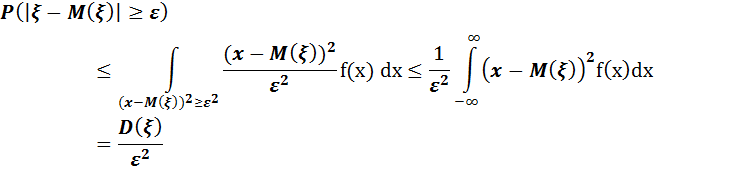
Сөйтіп (2) – теңсіздік дәлелденді
Кез – келген 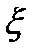 кездейсоқ шамада шекті дисперсия болып, кез – келген
кездейсоқ шамада шекті дисперсия болып, кез – келген 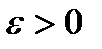 болғанда, онда мынадай теңсіздік орындалады:
болғанда, онда мынадай теңсіздік орындалады:
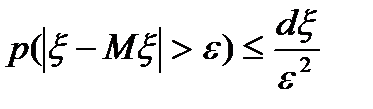 . (2.3.1)
. (2.3.1)
Бұл Чебышев теңсіздігі деп аталады.
50. Марков теңсіздігі. Дәлелдеу.
Марков теңсіздігін Чербышев леммасы деп те атайды.
Теорема. Егер  кездейсоқ шамасы тек қана оң мәндерді қабылдаса және математикалық күтімі бар болса, онда кез келген a оң сан үшін келесі теңсіздік орындалады:
кездейсоқ шамасы тек қана оң мәндерді қабылдаса және математикалық күтімі бар болса, онда кез келген a оң сан үшін келесі теңсіздік орындалады:
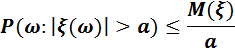
Дәлелдеу. Теңсіздіктің дәлелдеуін 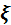 кездейсоқ шамасы үшін жүргіземіз:
кездейсоқ шамасы үшін жүргіземіз:
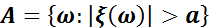
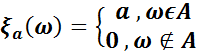
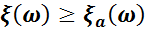
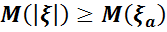
Соңғы теңдіктегі 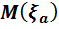 мынаған тең:
мынаған тең:  .
.
Осыдан

теңдігі шығады.
Теорема дәлелденді.
Марков теңсіздігі кез келген оң кездейсоқ шамалары үшін қолданылады.
51. Үлкен сандар заңы.
Үлкен сандар заңы деп кездейсоқ шамалардың арифметикалық ортасына қатысты тұжырымдалатын теоремалары айтамыз. Оларға Чебышев және Бернулли теоремалары жатады. Бұл теоремаларда өте көп кездейсоқ факторлардың жиынтық әсері, кездейсоқтықтан тәуелсіз нәтижелер алудың шарттары беріледі.
Чебышев теоремасы. Егер Х1, Х2,...., Хn- тәуелсіз кездейсоқ шамалар тізбегінің математикалық үміттері М(Хі) және бәрі бір С санымен шектелген дисперсиялары D(Хі) (і=1,2,3,.....,n) болса, онда кез келген 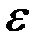 саны үшін
саны үшін 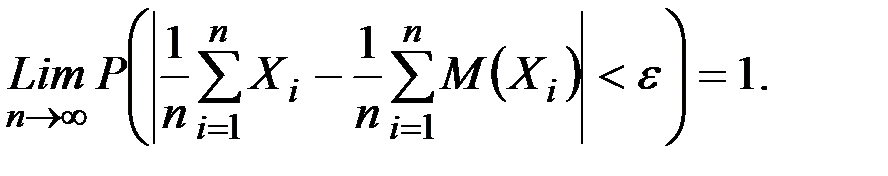
Чевышев теоремасын дәлелдеуде бағалау аламыз
 (3)
(3)
Салдар-1. (Бірдей үлестірімді кездейсоқ шамалар үшін Чевышев теорамасы.) Егер Чебышев теоремасының шартында X1, X2,...., Xn кездейсоқ шамалардың бір ғана М(Xі) =a математикалық үміті болса, онда

(2) –ден бағалау аламыз
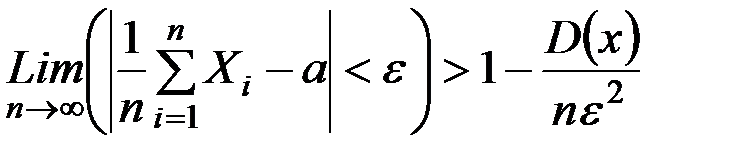 . (4)
. (4)
Салдар-2. (Бернулли теоремасы) Егер тәуелсіз n тәжірибенің әрқайсысында А оқиғасының пайда болу ықтималдығы р тұрақты болса, онда 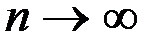 болғанда кез келген мейлінше аз оң
болғанда кез келген мейлінше аз оң 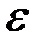 саны үшін
саны үшін
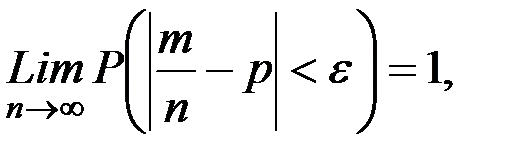
мұндағы 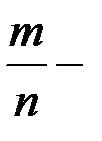 А оқиғасының пайда болуының салыстырмалы жиілігі.
А оқиғасының пайда болуының салыстырмалы жиілігі.
Бернулли теоремасын дәлелдеуден бағалау аламыз
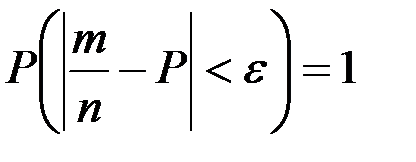
 . (5)
. (5)




52. Орталық шектік теорема. Қолданылу мысалдары.
Теорема.(Орталық шектік теорема) 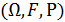 кеңістікте
кеңістікте  өзара тәуелсіз және бірдей үлестірілген және
өзара тәуелсіз және бірдей үлестірілген және 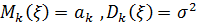
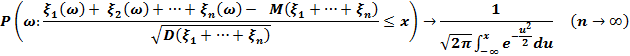
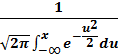 – стандартты нормаль үлестірім N(0;1)
– стандартты нормаль үлестірім N(0;1)

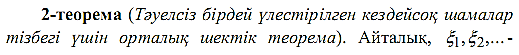
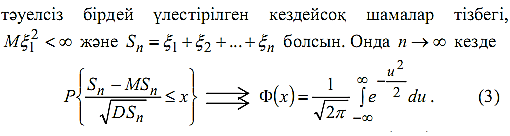
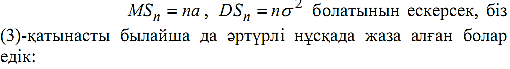

Қолданылу мысалдары



53. Математкиалық статистикадағы бас жиынтық және таңдама. Вариациялық қатар. Полигон. Гистограмма.
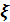 кездейсоқ шамасының мүмкін болатын барлық мәндерін бас жиынтық деп, n рет тәжірибе жүргізгенде пайда болған
кездейсоқ шамасының мүмкін болатын барлық мәндерін бас жиынтық деп, n рет тәжірибе жүргізгенде пайда болған  шамасының
шамасының 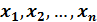 мәндерін статистикалық қатар деп атайды.
мәндерін статистикалық қатар деп атайды.
Қатар элементтерін өсу тәртібі бойынша орналастырғаннан кейін шыққан
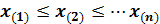 қатарын вариациялық қатар деп, ал оның элементтерін варианттар деп атайды.
қатарын вариациялық қатар деп, ал оның элементтерін варианттар деп атайды.
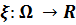 бақыланатын кездейсоқ шама. Оның үлестірім функциясы
бақыланатын кездейсоқ шама. Оның үлестірім функциясы 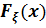 , бірақ бізге ол белгісіз.
, бірақ бізге ол белгісіз.
Бұл 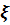 - деналынған көлемі n-ге тең таңдама. Сонымен көлемі n-ге тең таңдама дегеніміз өзара тәуелсіз және
- деналынған көлемі n-ге тең таңдама. Сонымен көлемі n-ге тең таңдама дегеніміз өзара тәуелсіз және 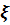 бірдей үлестірілген n кездейсоқ шама.
бірдей үлестірілген n кездейсоқ шама.
Дата добавления: 2015-01-29; Мы поможем в написании ваших работ!; просмотров: 8334 | Нарушение авторских прав Лучшие изречения:






