Экспоненциальный закон надежности

Зависимость опасности отказов от времени очевидно может быть трех типов:

1. Опасность отказов с увеличением времени эксплуатации убывает.

Элемент в процессе эксплуатации улучшает свои надежностные характеристики. Этот редкий случай имеет место, например, в процессе предварительной приработки, когда в начальный период эксплуатации отказавшие, бракованные элементы заменяются новыми. Сформированная так партия элементов улучшает свои характеристики надежности.

2. Опасность отказов с увеличением времени эксплуатации увеличивается. Элемент в процессе эксплуатации ухудшает свои характеристики надежности. Элемент «стареет». Это очевидный, наиболее распространенный случай.

3. Опасность отказов в процессе эксплуатации не меняется, остается постоянной. Элемент в процессе эксплуатации «не стареет», остается «новым». Очевидно, что это некая теоретическая модель.

Рассмотрим подробнее последний случай. Если λ(t)=const, то согласно (1.10) получим

(2.1)

Полученный закон надежности называется экспоненциальным и имеет большое значение в теории надежности. Частота отказов в соответствии с (1.3) равна

(2.2)

Средняя наработка на отказ согласно (1.11) равна

(2.3)

Вычислим вероятность надежной работы на интервале, равном среднему времени отказов t =T₀.

 

Надежность очень мала, примерно только треть элементов останется работоспособными. Поэтому для ответственных элементов время эксплуатации следует выбирать много меньше среднего времени жизни элемента (t <<T₀). Тогда вероятность безотказной работы согласно (2.1) примерно равна

(2.4)

а вероятность отказа примерно равна

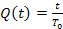(2.5)

Вероятность отказа на малом интервале времени ∆t у исправного элемента равна λ∆t. Эта вероятность не зависит от проработанного времени, если элемент исправен, то его дальнейшее поведение не зависит от прошлой предыстории. Верно и обратное утверждение. Для моделей отказов, когда предыстория не влияет на поведение отказов, справедлив экспоненциальный закон надежности. Такие модели отказов называются схемой мгновенных повреждений.

Рис.2.1 Модель мгновенных повреждений.

 

Пусть на элемент воздействует случайная ударная перегрузка (рис 2.1). Когда она меньше критической ∆, отказа нет, нет никаких мелких повреждений, ухудшающих надежностные характеристики. Элемент остается по всем показателям как «новый». Как только перегрузка превышает критический уровень, элемент отказывает. Если перегрузка представляет собой случайный процесс типа белого шума, все отсчеты которого независимы, предыстория эксплуатации на момент отказа не влияет. То есть такая модель отказа соответствует экспоненциальному закону надежности.

Недостаток экспоненциального закона в том, что он отражает редко встречающую модель отказов. Однако далее будет показано, что только этот закон позволяет построить практически применимые, инженерные методы расчетов.

Рис.2.2. Схема с переменным порогом.

 

Рассмотрим еще одну схему мгновенных повреждений, но с переменным во времени порогом (рис. 2.2). Эта схема отличается от схемы, приведенной на рис 2.1 тем, что порог – граница допустимых перегрузок переменный. Вначале он велик и перегрузка никогда не может его достигнуть. Затем порог снижается и в некоторый момент времени t₀ фиксируется на некотором постоянном значении, которое достигается перегрузкой.

Имеем при t<t₀ элемент не отказывает P(t)=1.

При t>t₀ имеем экспоненциальный закон надежности P(t)=e^-λ(t-t0)

График вероятности безотказной работы показан на рис. 2.3.

Рис.2.3. Закон с переменным порогом.

Для плотности вероятности отказа имеем (см. рис. 2.4):

при t<t₀ q(t)=0

при t>t₀ q(t)=λe^-λ(t-t0)

Рис.2.4. Опасность отказа.

 

Эта модель может служить приближением для результатов экспериментального определения закона надежности, полученного в виде, показанного на рис. 2.5.

Рис.2.5. Экспериментальная кривая частоты отказов.

 

 

Контрольные вопросы

1. Что такое экспоненциальный закон надежности?

2. В каком соотношении находятся среднее время безотказной работы и реальное время эксплуатации?

3. Опишите модель мгновенных повреждений.

 

3. Модель накопления повреждений. Гамма – распределение времени безотказной работы

Модель накопления повреждений предполагает, что действие возмущений в процессе эксплуатации, износ элемента все время накапливается, увеличивается. Это накопление может начинаться от разных начальных условий из-за случайных мелких дефектов производства, может нарастать с разной скоростью из-за случайного характера воздействий и т. д.

Предположим, что существует некоторый постоянный порог, по достижении которого происходит отказ (рис.3.1).

Рис.3.1. Модель накопления повреждений.

 

Рассмотрим следующую модель накопления повреждений (рис 3.2).

Рис.3.2. Принятая схема накопления повреждений.

 

В случайные независимые моменты времени скачком происходит увеличение повреждения. Все скачки равны по амплитуде. Примем величину скачка, равной a. Примем также, что соотношение между скачком и порогом таково, что отказ произойдет после r скачков. Пусть времена скачков образуют простейший поток событий, то есть удовлетворяют следующим условиям: события независимы; поток стационарный; в один момент времени может произойти только один скачок. Известно, что для простейшего потока или потока Пуассона, вероятность наступления точно k событий за время T равна

(3.1)

Здесь α - средняя частота скачков.

Отказ наступит после некоторого целого числа скачков r. Тогда P(t) - функция надежности есть вероятность того, что за время t произойдет меньше чем r скачков

(3.2)

Найдем плотность вероятности отказов для такого распределения

3.3)

Получен двухпараметрический (α,r) закон надежности, которым можно было бы аппроксимировать экспериментальные характеристики. Но для этого надо распространить (3.3) на непрерывные значения r. В принципе в (3.3) r может быть непрерывным всюду кроме аргумента факториала.

Существует гамма-функция, которая для целых положительных значений аргумента совпадает со значением факториала, и может быть принята как распространение понятия факториала на нецелые значения аргумента.

Выражение для гамма-функции есть

(3.4)

Для целых положительных r значение гамма-функции равно

Г(r)=(r−1)! (3.5)

Заменяя в (3.3) факториал на гамма-функцию, получим

(3.6)

Тогда для непрерывных значений r вероятность отказов равна

(3.7)

а функция надежности равна

(3.8)

Для средней наработки на отказ имеем

(3.9)

Здесь сделана подстановка x=ατ, следовательно dτ=dx/α.

Для гамма-функции имеет место рекуррентное соотношение, которое следует из (3.5):

Γ(r+1)=rΓ(r) (3.10)

Тогда для среднего времени жизни из (3.9) имеем:

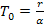(3.11)

Обратим внимание, что полученный результат согласуется с результатами для экспоненциального закона. Для модели мгновенных повреждений достаточно одного события – достижения порога (r=1), которое не зависит от предыстории процесса, чтобы произошел отказ. Средняя частота событий в пуассоновском потоке α по вероятности равна величине, обратной среднему времени между отказами 1/T_0e для экспоненциального закона надежности. Следовательно,

α =λ_e.

Тогда для экспоненциального закона из (3.11) получаем известный нам результат

Для дисперсии времени жизни имеем

(3.12)

Здесь учтено, что согласно (3.10)

Γ(r+2)=(r+1)Γ(r+1)=(r+1)rΓ(r).

Тогда

= (3.13)

Опасность отказа равна:

Опасность отказа для этого закона надежности вычисляется сложным образом. Однако при малых временах можно принять P(t)≈1; e^-αt≈1, тогда из (3.6) следует, что зависимость опасности отказа от времени имеет вид λ(t)≈At^r-1, что позволяет оценить поведение опасности отказа на начальном интервале. Точные зависимости показаны на рис 3.3.

Рис.3.3. Зависимость опасности отказов от параметра.

 

При r >1 имеем модель стареющих элементов (опасность отказов увеличивается). При r =1 имеем экспоненциальный закон надежности. Это соответствует модели мгновенных повреждений. Одного скачка достаточно для отказа. При r<1 имеем убывающую опасность отказа. Частота отказов представлена на рис.3.4. В пределе при r→∞ закон гамма- распределения стремится к нормальному закону надежности.

Рис.3.4. Плотность вероятности отказов – частота отказов.

 

 

Контрольные вопросы

1. Опишите модель повреждений закона гамма-распределения времени безотказной работы?

2. Ч то такое гамма-функция, зачем она используется при описании закона гамма-распределения?

3. Какой вид имеет зависимость опасности отказа от времени при законе гамма-распределения?