РАСЧЕТ НАДЕЖНОСТИ ИНФОРМАЦИОННОЙ СИСТЕМЫ
По структурной схеме надежности информационной системы и заданным значениям интенсивности отказов ее элементов:
1) построить график изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня 0,1 – 0,2;
2) определить время наработки системы соответствующее заданному γ (гамма-процентному ресурсу системы);
3) обеспечить при заданном γ (гамма-процентном ресурсе) увеличение времени наработки системы не менее чем в 1,5 раза за счет структурного резервирования элементов системы. Варианты структурных схем и значения интенсивностей отказов приведены на рис. 7 и в табл. 2, соответственно.
Рис. 1 - Структурная схема надежности
Значения интенсивности отказов элементов,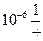 
:
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
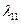
| 0,01 | 0,1 | 0,1 | 0,2 | 0,2 | 0,5 | 0,5 | 0,3 |
где γ – (гамма-процентный ресурс системы) – вероятность безотказной работы системы, выраженный в процентах, по истечении определенного времени непрерывной работы (наработки) системы.
Все элементы системы работают в режиме нормальной эксплуатации. Резервирование отдельных элементов или групп элементов должно осуществляться идентичными по надежности резервными элементами или группами элементов. Переключатели при резервировании считаются идеальными. На схемах обведенные пунктиром m элементов являются функционально необходимыми.
Расчет
1. Элементы 4, 5, 6 и 7 образуют соединение «2 из 4», которое заменяем элементом А. Так как p 4 = p 5 = p 6 = p 7, то для определения вероятности безотказной работы элемента А можно воспользоваться выражением, в основе которого лежит формула биноминального распределения (биноминальному распределению подчиняется дискретная случайная величина k – число появлений некоторого события в серии из n опытов, если в отдельном опыте вероятность появления события составляет p).
где 
– биноминальный коэффициент, называемый «числом сочетаний по k из n» (т. е. сколькими разными способами можно реализовать ситуацию k из n).
.
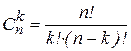Поскольку для отказа системы «m из n» достаточно, чтобы количество исправных элементов было меньше m, вероятность отказа может быть найдена по теореме сложения вероятностей для k = 0, 1, …, (m – 1):
Аналогичным образом можно найти вероятность безотказной работы как сумму для k = m, m + 1, …, n:
.
В данном конкретном случае, при n = 4 и m = 2, вероятность безотказной работы элемента F определится выражением:
|
2. В исходной схеме элементы 10, 11 и 12 образуют параллельное соединение. Заменяем их квазиэлементом В. Учитывая, что p10 = p11 = р12 получим:
(2)
3. Элементы 13 и 14 также образуют параллельное соединение, заменив которое элементом С и учитывая, что p13 = p14, получим:
(3)
7.
рис. 2 - Преобразованная схема
8. Элементы 2, 3, А, 8, 9 (рис. 2) образуют мостиковую систему, которую можно заменить квазиэлементом D. Для расчета вероятности безотказной работы воспользуемся методом минимальных путей. Логическая схема мостиковой системы по методу минимальных путей приведена на рис. 3
 |
Система, изображенная на рис. 3 работоспособна до тех пор, пока работоспособны элементы 2 и 8 или 3 и 9, или – 2, А и 9, или – 3, А и 8. Таким образом, вероятность работы квазиэлемента D можно определить по формуле:
(4)
9.
Рис. 4 - Схема после преобразования
10. В преобразованной схеме (рис. 4) элементы 1, D, B, C и 15 образуют последовательное соединение. Тогда вероятность безотказной работы всей системы определяется выражением:
(5)
11. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 15 (рис. 1) подчиняются экспоненциальному закону:
(6)
12. Результаты расчетов вероятностей безотказной работы элементов 1 – 15 исходной схемы по формуле (9) для наработки до 3·106 часов представлены в табл. 1:
Таблица 1
| Наработка, t – 100 000 ч | |||||||||
| Элемент | 
| 0,5 | 1,5 | 2,5 | 2,25 | ||||
| 0,01 | 0,9995 | 0,9990 | 0,9985 | 0,9980 | 0,9975 | 0,9970 | 0,9978 | ||
| 2, 3 | 0,1 | 0,9950 | 0,9900 | 0,9851 | 0,9802 | 0,9753 | 0,9704 | 0,9778 | |
| 4 - 7 | 0,6065 | 0,3679 | 0,2231 | 0,1353 | 0,0821 | 0,0498 | 0,1054 | ||
| 8, 9 | 0,2 | 0,9900 | 0,9802 | 0,9704 | 0,9608 | 0,9512 | 0,9418 | 0,9560 | |
| 10 - 12 | 0,6065 | 0,3679 | 0,2231 | 0,1353 | 0,0821 | 0,0498 | 0,1054 | ||
| 13, 14 | 0,5 | 0,9753 | 0,9512 | 0,9277 | 0,9048 | 0,8825 | 0,8607 | 0,8936 | |
| 0,3 | 0,9851 | 0,9704 | 0,9560 | 0,9418 | 0,9277 | 0,9139 | 0,9347 | ||
| A | - | 0,8282 | 0,4687 | 0,2173 | 0,0911 | 0,0361 | 0,0139 | 0,0577 | |
| B | - | 0,9391 | 0,7474 | 0,5311 | 0,3535 | 0,2266 | 0,1420 | 0,2840 | |
| C | - | 0,9994 | 0,9976 | 0,9948 | 0,9909 | 0,9862 | 0,9806 | 0,9887 | |
| D | - | 1,0000 | 0,9997 | 0,9988 | 0,9972 | 0,9951 | 0,9928 | 0,9962 | |
| P | - | 0,9241 | 0,7227 | 0,5037 | 0,3283 | 0,2058 | 0,1260 | 0,2609 | |
| B' | - | 0,9994 | 0,9745 | 0,8673 | 0,6875 | 0,4960 | 0,3354 | 0,5898 | |
| P' | - | 0,983447 | 0,94227 | 0,822595 | 0,638548 | 0,450478 | 0,297511 | 0,541728 | |
13. Результаты расчетов вероятностей безотказной работы квазиэлементов А, В, С, D, по формулам (1) – (4) и также представлены в табл. 1.
14.
Рис. 5 - График зависимости вероятности безотказной работы системы Р от времени (наработки) t
15. По графику (рис. 5, кривая Р) находим для γ = 50% (Р = 0.5) γ-процентную наработку системы t = 1,5·105 ч, расчет при t = 1,5·105 ч показывает (табл. 1), что P γ = 0,5037 ~ 0,5.
17. По условиям задания находим время, превышающее в 1,5 раза время, соответствующее вероятности безотказной работы, равное 0,5 (P γ = 0,5):
. (10)
= 1,5·1,5·106 = 2,25·106 ч.
18. Расчет показывает (табл. 1), что при = 2,25·105 ч для элементов преобразованной схемы (рис. 4) p1 ( ) =0,9978, pD ( ) =0,9962, pB ( ) = 0,2840, pC ( ) = 0,9887, p15 ( ) = 0,9347. Следовательно, из пяти последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент В, и именно увеличение его надежности даст максимальное увеличение надежности системы в целом.
19. Для того чтобы при = 2.25 × 105 ч система в целом имела вероятность безотказной работы P’ = 0,5, надо найти необходимую вероятность безотказной работы элемента F. Так как
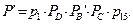
где 
– необходимая вероятность безотказной работы элемента В, то
(11)
20. Для элемента В резервирование означает увеличение общего числа элементов. Аналитически определить минимально необходимое количество элементов достаточно сложно, так как число элементов должно быть целым и функция 
= f(n) дискретна.
21. Для повышения надежности параллельно добавляем элементы, идентичные по надежности исходным элементам 10 – 12, до тех пор, пока вероятность безотказной работы квазиэлемента В не достигнет заданного значения:
- добавляем элемент 16, получаем:
- добавляем элемент 17, получаем:
- добавляем элемент 18, получаем:
- добавляем элемент 19, получаем:
- добавляем элемент 20, получаем:
22. Таким образом, для повышения надежности до требуемого уровня, необходимо в исходной схеме (рис. 1) квазиэлемент В достроить элементами 16, 17, 18, 19 и 20 (рис. 6).
рис.6
23. Результаты расчетов вероятностей безотказной работы квазиэлемента «В'» и системы в целом Р’ представлены в табл. 1.
24. Расчеты показывают, что при t’ = 2,25×105 ч, Р’ = 0,5417 > 0,5, что соответствует условию задания.
Расчет основной схемы
1. Построение основной схемы без резервных элементов осуществляется по основным элементам системы: 1, 2, 8, 10, 13, 15 (рис. 7) или 1, 2, А, 9, 12, 13, 15 (рис. 8), т.к. остальные элементы имеют такие же параметры, как и элементы, которые они резервируют:
рис. 7 - Первый вариант основной схемы
рис. 8 - Второй вариант основной схемы
2. Проверим вероятность безотказной работы первого и второго варианта основной схемы по формуле:
и 
(т.к. соединение последовательное)
Таблица 2
| Вероятность | Время tх100000 с | |||||
| 0,5 | 1,5 | 2,5 | ||||
| Р1 | 0,5767 | 0,3325 | 0,1918 | 0,1106 | 0,0638 | 0,0368 |
| Р2 | 0,3498 | 0,1223 | 0,0428 | 0,0150 | 0,0052 | 0,0018 |
3. Наибольшую вероятность безотказной работы имеет первый вариант основной схемы, значит в качестве основной схемы системы принимаем его. Произведем расчет для основной схемы системы.
Таблица 3
| Наработка, t – 100 000 ч | |||||||||
| Элемент |
| 0,5 | 1,5 | 2,5 | 0,63 | 0, 945 | |||
| 0,01 | 0,9995 | 0,9990 | 0,9985 | 0,9980 | 0,9975 | 0,9970 | 0,9994 | 0,9991 | |
| 0,1 | 0,9950 | 0,9900 | 0,9851 | 0,9802 | 0,9753 | 0,9704 | 0,9937 | 0,9906 | |
| 0,2 | 0,9900 | 0,9802 | 0,9704 | 0,9608 | 0,9512 | 0,9418 | 0,9875 | 0,9813 | |
| 0,6065 | 0,3679 | 0,2231 | 0,1353 | 0,0821 | 0,0498 | 0,5326 | 0,3887 | ||
| 0,5 | 0,9753 | 0,9512 | 0,9277 | 0,9048 | 0,8825 | 0,8607 | 0,9690 | 0,9538 | |
| 0,3 | 0,9851 | 0,9704 | 0,9560 | 0,9418 | 0,9277 | 0,9139 | 0,9813 | 0,9720 | |
| P | - | 0,9241 | 0,7227 | 0,5037 | 0,3283 | 0,2058 | 0,1260 | 0,4998 | 0,3533 |
| 10' | - | 0,9391 | 0,6004 | 0,3965 | 0,2524 | 0,1574 | 0,0971 | 0,7815 | 0,6263 |
| P' | - | 0,8884 | 0,5373 | 0,3357 | 0,2021 | 0,1193 | 0,0696 | 0,7287 | 0,5639 |
рис. 9 - График зависимости вероятности безотказной работы системы Р от времени (наработки) t
4. По графику (рис. 9, кривая Р) находим для γ = 50% (Р = 0.5) γ-процентную наработку системы t = 0,63·105 ч, расчет при t = 0,63·105 ч показывает (табл. 1), что P γ = 0,4998 ~ 0,5.
5. По условиям задания находим время, превышающее в 1,5 раза время, соответствующее вероятности безотказной работы, равное 0,5 (P γ = 0,5):
. (10)
= 0,63·1,5·105 = 0,945·105 ч.
6. Расчет показывает (табл. 2), что при = 0,945·105 ч для элементов преобразованной схемы (рис. 4) p1 ( ) =0,9978, pD ( ) =0,9962, pB ( ) = 0,2840, pC ( ) = 0,9887, p15 ( ) = 0,9347. Следовательно, из пяти последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент В, и именно увеличение его надежности даст максимальное увеличение надежности системы в целом.
7. Для того чтобы при = 2.25 × 105 ч система в целом имела вероятность безотказной работы P’ = 0,5, надо найти необходимую вероятность безотказной работы элемента F. Так как
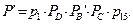
где – необходимая вероятность безотказной работы элемента В, то
(11)
8. Для элемента В резервирование означает увеличение общего числа элементов. Аналитически определить минимально необходимое количество элементов достаточно сложно, так как число элементов должно быть целым и функция = f(n) дискретна.
9. Для повышения надежности параллельно добавляем элементы, идентичные по надежности исходному элементу 10, до тех пор, пока вероятность безотказной работы квазиэлемента 10 не достигнет заданного значения:
- добавляем элемент 16, получаем:
рис. 10
10. Таким образом, для повышения надежности до требуемого уровня, необходимо в исходной основной схеме квазиэлемент 10 достроить элементом 16 (рис. 10).
Критерий Колмогорова
1. При применении критерия согласия Колмогорова в качестве меры расхождения между теоретическим и статистическим распределением рассматривается максимальное значение модуля разности между теоретической и экспериментальной функциями распределения.
На основе этого критерия, экспериментальное распределение согласуется
с выбранным теоретическим, если выполняется условие
где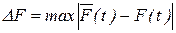 
– наибольшее отклонение теоретической кривой распределения от экспериментальной; n – общее количество экспериментальных данных.
2. В табл. 4 приведены вероятности отказов по экспериментальным данным 
и по теоретическому закону F(t).
Считаем закон распределения отказов экспоненциальным 
Таблица 4
| t,105 ч | 0,5 | 1,5 | 2,5 | |||
| 0,0759 | 0,2773 | 0,4963 | 0,6717 | 0,7942 | 0,8740 |
| 0,2953 | 0,5034 | 0,6501 | 0,7534 | 0,8262 | 0,8775 |
3. Количество экспериментальных данных n = 15
По данным таблицы строим теоретическую и экспериментальную кривые (рис 11).
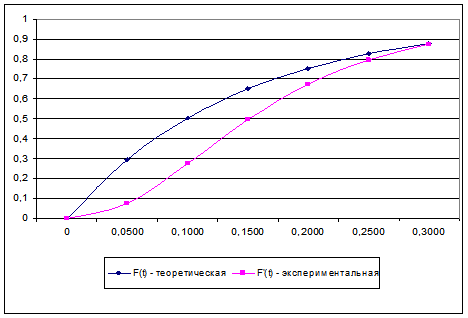
Рис. 11
Из рисунка и таблицы D F = 0.2261.
Проверяем по критерию согласия Колмогорова.
Считаем, что закон распределения отказов – экспоненциальный.
Критерий Колмогорова прост и нагляден.
Недостатком критерия является то, что он требует предварительного знания теоретического распределения, т. е. знания не только вида функции распределения F(t), но и ее параметров.
ВЫВОДЫ
1. По данным расчета вероятности безотказной работы системы от времени построен график P(t).
2. По графику найдено время, соответствующее 50% g-процентному ресурсу системы (t = 2,25 × 105 ч).
3. Для увеличения наработки системы в 1,5 раза при 50% g -процентном ресурсе системы предложено нагруженное резервирование основных элементов 10, 11, 12 идентичными по надежности резервными элементами 16, 17, 18, 19 и 20.
4. Рассчитана вероятность безотказной работы системы с повышенной надежностью от времени, построен график P’(t) системы с повышенной надежностью, на графике (рис. 7) показано время (t’ = 2,25 × 105 ч) соответствующее 50% g -процентному ресурсу.
Расчет надежности системы
1. Пусть есть система, представляющая собой соединение двух компьютеров с сервером. Можно выделить следущие элементы системы:
 - База данных
|  - Персональный компютер
|  - Сервер
|
 - Линия связи от ПК до свича
|  - Свич
|  - Программа
|
 - Клиентская часть программы
|  - Линия связи с сервером
|
Под отказом системы будем предполагать отказ на запрос пользователя.
2. Из представленных элементов можно составить следущую схему системы:
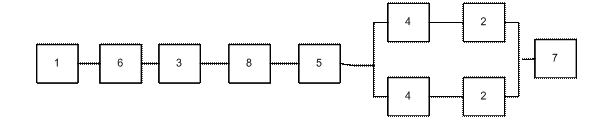
рис. 1 - Структурная схема соединения элементов
3. Элементы 4 и 2 образуют последовательное соединение, заменив которое элементами А и И, получим:
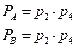
4. Элементы В и С образуют параллелльное соединение, заменим его на соединение D:
5. Получаем схему следущего вида:
рис. 2 - Преобразованная стуктурная схема
6. Вероятность безотказной работы системы будет расчитываться как произведение всех элементов преобразованной системы, так как все элементы соединины последовательно:
7. Необходимо определить интенсивности отказов элементов системы. Время наработки примем равным 
.
8. Программная часть системы является самой надежной частью, при наличии защиты программной части от влияния пользователя отлаженная программа практически полностью исключает ошибки. Предположим, что интенсивность наработки на отказ программы и киентской части программы 
. Надежность базы данных зависит от надежности жесткого диска, на котором она хранится. Тогда, изучив документацию от производителя, можно воспользоваться их рассчетами и приянть интенсивность наработки на отказ равную 
. Наработку на отказ персональных компьютеров производители расчитывают и называют в пределах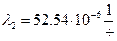 
. Сервером является ПК с более мощными и современными параметрами, наработка на отказ наиболее современного компьютера на данный момент составляет 
. Наработку на отказ для кабелей длиной до 100 м при изгибах производители дают равной 
. Наработку на отказ соединительной линии к серверу примем так же равной 
. Самым уязвивым элементом системы является свич, наработка на отказ которого на прямую зависит от количества элементов, подключенных в него, поэтому интенсивность наработки на отказ свича примем равной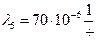 
9. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 8 (рис. 1) подчиняются экспоненциальному закону: (1)
10. Результаты расчетов вероятностей безотказной работы элементов 1 – 8 исходной схемы по формуле (1) для наработки до 3·104 часов представлены в табл. 1:
| Элемент | λ, 10-6 | Наработка, t  10000 ч
| |||||
| 0,0050 | 0,0100 | 0,0150 | 0,0200 | 0,0250 | 0,0300 | ||
| 0,9950 | 0,9900 | 0,9851 | 0,9802 | 0,9753 | 0,9704 | ||
| 52,54 | 0,7690 | 0,5913 | 0,4547 | 0,3497 | 0,2689 | 0,2068 | |
| 0,8958 | 0,8025 | 0,7189 | 0,6440 | 0,5769 | 0,5169 | ||
| 0,2 | 0,9990 | 0,9980 | 0,9970 | 0,9960 | 0,9950 | 0,9940 | |
| 0,7047 | 0,4966 | 0,3499 | 0,2466 | 0,1738 | 0,1225 | ||
| 0,1 | 0,9995 | 0,9990 | 0,9985 | 0,9980 | 0,9975 | 0,9970 | |
| 0,1 | 0,9995 | 0,9990 | 0,9985 | 0,9980 | 0,9975 | 0,9970 | |
| 0,2 | 0,9990 | 0,9980 | 0,9970 | 0,9960 | 0,9950 | 0,9940 | |
| A | 0,7682 | 0,5901 | 0,4533 | 0,3483 | 0,2675 | 0,2055 | |
| B | 0,7682 | 0,5901 | 0,4533 | 0,3483 | 0,2675 | 0,2055 | |
| C | 0,9463 | 0,8320 | 0,7012 | 0,5752 | 0,4635 | 0,3688 | |
| P | 0,5932 | 0,3270 | 0,1727 | 0,0888 | 0,0449 | 0,0224 |
Рис. 3 - График зависимости вероятности безотказной работы системы Р от времени (наработки) t
