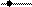, (20)
где 
.
Схема расчета надежности (рис. 3) представляет собой общее резервирование замещением с целой кратностью m.
| |||||||||
Основная цепь
Резервные цепи
 | |||||||||
 |  |  | |||||||
 |
Рис. 3
При экспоненциальном законе надежности и ненагруженном состоянии резерва вероятность безотказной работы системы:
(21)
где 
- интенсивность отказов основного (нерезервированного) устройства.
Средняя наработка системы до первого отказа:
(22)
где 
- средняя наработка до первого отказа основного (нерезервированного устройства).
Схема расчета надежности (рис. 4) представляет собой раздельное резервирование замещением с целой кратностью m.
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 |
Рис. 4
Вероятность безотказной работы системы:
(23)
где 
- вероятность безотказной работы системы i-го типа, резервированных по способу замещения.
Значение вычисляется по формуле общего резервирования замещением (21).
Пример решения задачи 4.2 для исходных данных:
Готовой формулы для средней наработки до первого отказа в рассматриваемом случае нет. Поэтому необходимо воспользоваться соотношением
Найдем выражение для вероятности безотказной работы 
системы. Очевидно, 
где
Тогда, подставляя значения 
в выражение для , получим
Так как
то
Подставляя в выражение для 
значение интенсивности отказов, получаем
Воспользовавшись известным соотношением (4), найдем зависимость
Функция 
приведена на рис. 5. Заметим, что интенсивность отказов резервированной системы при t = 0 равна 
, т.е. равна интенсивности отказов 
нерезервированного элемента.
  |
Рис. 5
При больших t интенсивность отказов стремится к величине 
т.е. к интенсивности отказов нерезервированной системы. Это свойство справедливо для сколь угодно сложных систем с любым видом резервирования.
Методические указания к теме 5
Составление графа переходов системы при m кратном резервировании рассмотрим на простом примере.
Пусть система состоит из основного элемента 1 и резервного элемента 2. Схема расчета надежности системы имеет вид, представленный на рис. 6.
 | |||||
 | |||||
 |
Рис. 6
В данном случае кратность общего резервирования m = 1.
Число состояний системы в общем случае равно m + 2, т.е. число состояний системы из двух элементов равно 3: состояние 0 – 2 элемента, входящих в систему работоспособны; состояние 1 – один из элементов, входящих в систему, в отказовом состоянии; состояние 2 – оба элемента, входящих в систему, в отказовом состоянии.
Граф состояний такой простейшей системы имеет вид, представленный на рис. 7.
 |
Рис.7. Граф состояний простейшей системы: 
- интенсивности отказов или переходов системы из состояний 0 – 1 и 1-2 соответственно;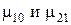 
- интенсивности восстановлений или обратных переходов из состояний 1 – 0 и 2 – 1
Состояния 0, 1, 2 называют узлами графа, а возможные переходы из одного состояния в другое называют ветвями графа.
Академик А.Н. Колмогоров предложил для определения вероятностей нахождения системы в каждом из состояний составлять и решать дифференциальные уравнения, которые и называются уравнениями массового обслуживания.
В инженерных расчетах систему этих уравнений можно получать непосредственно по виду графа состояний, применяя следующее правило: для каждого из возможных состояний системы записывается уравнение, в левой части которого 
а справа – столько слагаемых, сколько стрелок графа соприкасается с данным состоянием. Если стрелка направлена в данное состояние, то перед слагаемым ставится плюс, если стрелка направлена из данного состояния – минус. Каждое из слагаемых будет равно произведению интенсивности перехода из данного состояния (либо в данное состояние) на вероятность состояния, из которого выходит стрелка.
Согласно данному правилу, система дифференциальных уравнений для рассматриваемого графа состояний имеет вид
(24)
где 
- вероятности возможных состояний системы в 0-м, 1-м, и 2-м состояниях соответственно.
Полученную систему дифференциальных уравнений можно решить по известным правилам.
В инженерных расчетах решение системы упрощается, если учесть, что рассматриваемый процесс функционирования системы марковкий стационарный, для которого производные 
можно принять равными нулю (вероятности состояний не меняются с течением времени). Тогда система уравнений (24) переходит в систему алгебраических уравнений
(25)
Решение системы уравнений (25) имеет вид
В инженерных расчетах результаты решения системы уравнений (25) можно получить непосредственно по виду графа состояний, если применить следующее правило: вероятность нулевого состояния определяется выражением
где числитель правой части – всегда единица; знаменатель – сумма, состоящая из единицы и дробей, числители которых – произведения интенсивностей, изображенных на верхних стрелках, знаменатели - произведения интенсивностей на нижних стрелках (произведения формируются с последовательным увеличением числа множителей от одного до n в соответствии с переходами
.
Вероятность состояния 1 равна вероятности состояния 0 умноженной на коэффициент, равный второму слагаемому в знаменателе для 
, т.е. 
.
Вероятность состояния 2 равна вероятности состояния 0, умноженной на коэффициент, равный третьему слагаемому в знаменателе для , т.е.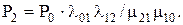 
Вероятность n–го состояния равна вероятности 0, умноженной на коэффициент, равный последнему (n-y) слагаемому в знаменателе для , т.е. 
.
После того как будут определены вероятности всех возможных состояний системы, можно определить коэффициент технической готовности системы 
. 
где n – последнее исправное состояние системы.
Для рассматриваемого простейшего случая 
.
Содержание контрольной работы
Тема 1. Расчет количественных характеристик надежности невосстанавливаемых и восстанавливаемых элементов систем электроснабжения.
Задача 1.1. На испытания поставлено 
элементов. За время t, час, вышло из строя n(t) штук элементов. За последующий интервал времени 
вышло из строя 
элементов. Вычислить вероятность безотказной работы за время 
, за время 
, частоту отказов 
и интенсивность отказов 
на интервале .
Исходные данные приведены в табл. 2.
Задача 1.2. На испытании находилось 
образцов неремонтируемой электроаппаратуры. Число отказов фиксировалось через каждые 1000 час. работы 
. Данные об отказах приведены в табл. 3. Вычислить количественные характеристики надежности 
и среднее время безотказной работы 
, предположив, что на испытаниях находились только те образцы, которые отказали.
Построить зависимости характеристик от времени.
Таблица 2
| № вариантов | Исходные данные | ||||
|
| t, час |  час
| 
|
| |
Таблица 3
| Варианты 
| |||||||||
| 0 - 1000 | ||||||||||
| 1000 - 2000 | ||||||||||
| 2000 - 3000 | ||||||||||
| 3000 - 4000 | ||||||||||
| 4000 - 5000 | ||||||||||
| 5000 - 6000 | ||||||||||
| 6000 - 7000 | ||||||||||
| 7000 - 8000 | ||||||||||
| 8000 - 9000 | ||||||||||
| 9000 - 10000 |
Задача 1.3. Известно, что интенсивность отказов силового трансформатора в период его нормальной эксплуатации 
, отказа/год, а среднее время восстановления 
, сутки.
Требуется вычислить функцию, готовности 
коэффициент готовности трансформатора 
и вероятность застать трансформатор в исправном состоянии после t лет его нормальной эксплуатации P(t).
Исходные данные приведены в таблице 4.
Таблица 4
| № вариантов | , отказа/год
| , сутки
|  , лет
|
| 0,5 | |||
| 0,6 | |||
| 0,7 | |||
| 0,8 | |||
| 0,9 | |||
| 0,4 | |||
| 0,55 | |||
| 0,65 | |||
| 0,75 |
Тема 2. Экспоненциальный закон распределения времени безотказной работы элементов систем электроснабжения.
Задача 2.1. Система электроснабжения состоит из N элементов, имеющих разную надежность. Известно, что каждый из элементов, проработав вне системы 
, имел 
отказов. Для каждого из элементов справедлив экспоненциальный закон надежности.
Определить наработку на отказ всей системы электроснабжения 
, час. Исходные данные для решения задачи приведены в табл. 5.
Таблица 5
| № варианта | Исходные данные | ||||||||||
| N |
 час
|
|
 час
|
|
 , час
|
|
 час
|
|
 час
|
| |
| - | - | - | - | ||||||||
| - | - | ||||||||||
| - | - | - | - | ||||||||
| - | - | ||||||||||
| - | - | - | - | ||||||||
| - | - | ||||||||||
| - | - | - | - |
Задача 2.2. Интенсивность отказов автоматического воздушного выключателя 
. Определить вероятность безотказной работы выключателя в течение t, час, с начала периода нормальной эксплуатации в системе электроснабжения 
, частоту отказов 
, 1/час и среднюю наработку до первого отказа 
, час. Исходные данные для решения задачи приведены в табл. 6.
Таблица 6
| № вариантов | , отказа / год
| t, час |
| 0,7 | ||
| 0,2 | ||
| 0,6 | ||
| 0,3 | ||
| 0,5 | ||
| 0,4 | ||
| 0,9 | ||
| 0,8 | ||
Тема 3. Расчет количественных характеристик надежности при основном соединении элементов электроснабжения.
Задача 3.1. Блок питания релейной защиты системы электроснабжения состоит из элементов, номенклатура и режим работы которых приведены в табл. 7. Требуется определить среднюю наработку до первого отказа и вероятность безотказной работы в течение t, час 
.
Тема 4. Расчет характеристик надежности резервированной системы.
Задача 4.1. Схемы расчета надежности резервированной системы, состоящей из элементов 
приведены в табл. 8. Определить вероятность безотказной работы системы 
, если известны вероятности безотказной работы элементов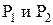 
.
Таблица 7
| Наименование и тип элемента |
Количество элементов 
№ вариантов
| Интенсивность отказов при номинальном режиме
 , 1/час
| Режим работы | Поправочный коэффициент аi | t, час № вариантов | |||||||||
Коэффи-циент нагрузки
| Темпера-
тура среды, 
| |||||||||||||
| Резистор МЛТ, 1 Вт | 0,2 | 0,4 | ||||||||||||
| Резистор МЛТ, 0,5 Вт | 0,5 | 0,8 | 1,86 | |||||||||||
| Резистор ПЭВ, 10 Вт | 3,2 | 0,2 | 0,14 | |||||||||||
| Резистор СПО, 2 Вт | 1,8 | 0,8 | 1,38 | |||||||||||
| Конденсатор МБМ | 0,3 | 0,38 | ||||||||||||
| Диоды выпрямительные | 0,5 | 1,05 | ||||||||||||
| Трансформа торы силовые | 5,2 | |||||||||||||
| Дроссель | 0,8 | 4,1 |
Задача 4.2. Система электроснабжения (см.рисунок 8) состоит из двух повышающих трансформаторов 
линии электропередачи 
и двух понижающих трансформаторов 
. Трансформаторы 
могут пропустить по 100 % потребной мощности каждый. Для повышения надежности трансформаторов применяется нагруженный резерв, т.е. при отказе одного из трансформаторов питание потребителя обеспечивает оставшийся в работе трансформатор.
Схема расчета надежности приведена на рисунке 9.
Рассчитать вероятность безотказной работы системы электроснабжения и ее среднюю наработку до первого отказа, а также построить зависимость от времени частоты отказов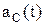 
и интенсивность отказов системы. Предполагается, что последействие отказов элементов отсутствует.
Таблица 8
| № п/п | Схема расчета надежности | № варианта | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Р1
 
| 0,8/0,7 | 0,6/0,9 | 0,6/0,7 | 0,5/0,75 | 0,8/0,95 | 0,5/0,7 | 0,45/0,85 | 0,8/0,6 | 0,9/0,5 | 0,9/0,4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Р1 Р2
| 0,8/0,9 | 0,6/0,7 | 0,5/0,8 | 0,9/0,95 | 0,8/0,98 | 0,72/0,88 | 0,55/0,7 | 0,8/0,6 | 0,9/0,5 | 0,8/0,5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Р1
| 0,6/0,98 | 0,5/0,97 | 0,6/0,96 | 0,5/0,95 | 0,4/0,94 | 0,3/0,93 | 0,2/0,92 | 0,7/0,91 | 0,7/0,9 | 0,6/0,8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||
| |||||
 |
Рис.9. Схема расчета надежности
Таблица 9
Исходные данные для решения задачи
| Обозначения элементов |  1/час, для вариантов задачи
| ||||||||||||||||||
| на схеме эл.снаб- жения | на схеме надеж- ности | ||||||||||||||||||
| 
| 0,8 | 0,5 | 0,4 | 0,5 | 0,5 | 0,3 | 0,5 | 0,3 | ||||||||||
| 
| 0,5 | 0,5 | 0,4 | 0,4 | 0,5 | 0,3 | 0,3 | 0,5 | ||||||||||
| 
| 0,8 | 0,5 | 0,4 | 1,5 | 0,5 | 0,3 | 0,5 | |||||||||||
Тема 5. Расчет характеристик надежности восстанавливаемых элементов методами теории массового обслуживания.
Задача 5.1. Для питания поселка используются электроагрегат из 
генераторов. Каждый из генераторов обладает мощностью, достаточной для обеспечения питания поселка. Эти генераторы работают поочередно. При отказе работающего генератора (или соответствующих устройств регулирования и коммутации) в работу включается резервный генератор, а отказавший отключается и ремонтируется. Отказ электроагрегата состоит в прекращении питания поселка. Конструкция электроагрегата допускает одновременный ремонт всех генераторов. При обслуживании генератора имеется нужное число ремонтников.
Изобразить граф состояний системы электроснабжения, составить уравнения массового обслуживания и определить коэффициент готовности агрегата.
Таблица 10
Исходные данные для решения задачи
| № вариантов | , шт.
| ,час
(наработки на отказ генератора)
| , час
(среднее время восстановления генератора)
|
