Из таблицы 2 (Приложение 2) по заданным n и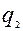 
определяют два числа 
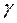и m Гипотеза о нормальности принимается, если не более m разностей 
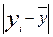превосходят 
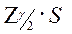, где S рассчитывается по формуле (5), 
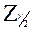- квантиль нормированной функции Лапласа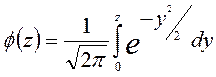 
См. таблицу 3 (Приложение 2)
Гипотеза о нормальности принимается только в том случае, если для проверяемой группы результатов наблюдений выполняются оба критерия. Уровень значимости составного критерия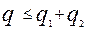 
, где 
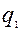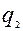, - уровни значимости для 1 и 2 критерия соответственно.
4. Определить наличие грубых погрешностей, и если последние обнаружены, соответствующие результаты отбросить и повторить вычисления. Сначала следует проверить, не являются ли максимальное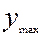 
и минимальное 
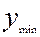значения выборки 
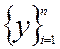результатами наблюдений с грубыми погрешностями. Приведем критерий такой проверки. Если U<П, то результатов наблюдений с грубыми погрешностями в выборке нет, если U>П, то максимальный или минимальный член (в зависимости от того, который из них обеспечивает наибольшее значение U) является результатом наблюдений с грубой погрешностью.
Здесь
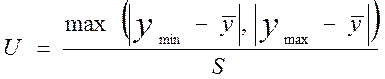, (10)
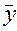и S рассчитываются по формулам (4) и (5) соответственно 
; 
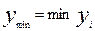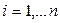
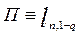- квантили распределения, приведенные в зависимости от (1-q) и n в таблице 4 Приложения 2.
После проверки по указанному критерию результат наблюдений с грубой погрешностью устраняют из выборки и вновь повторяют всю процедуру. Так действуют до тех пор, пока все результаты наблюдений с грубыми погрешностями не будут устранены.
5. Определить оценку величины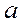 
. Обозначим оценку величины 
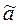. Поскольку выборочные средние 
, 
,… 
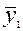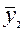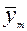являются оценками величин 
, 
,… 
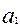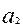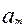, входящих в формулу (3) обозначим их 
, 
,… 
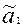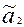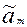. Тогда оценку величины 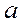можно определить по формуле
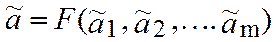. (11)
6. Вычислить доверительные границы случайной составляющей погрешности результатов многократных измерений для всех величин 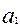, ,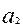… , 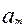подвергаемым прямым измерениям и входящим в зависимость (3)
Доверительную границу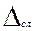 
(без учёта знака) случайной погрешности результата измерения находят по формуле
, 
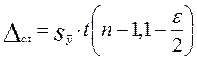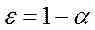, (12)
где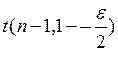 
- квантиль распределения Стьюдента, который в зависимости от доверительной вероятности 
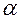и числа результатов наблюдений находят по таблице 5 Приложение 2
7. Вычислить доверительные границы неисключенной систематической погрешности (НСП) результатов измерений для каждой величины 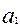, ,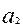… 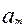НСП результата образуется из составляющих, в качестве которых могут быть НСП метода, средств измерений, а также вызванные другими источниками. При суммировании составляющих НСП результата измерения все они рассматриваются, как случайные величины. При отсутствии данных о виде распределения этих случайных величин их распределения принимают за равномерные. Доверительную границу НСП 
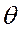результата измерения при равномерном распределении НСП (без учёта знака) можно вычислить по формуле
, 
, 
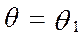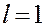
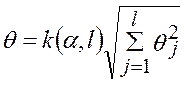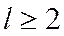, (13)
где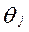 
- граница j – ой НСП
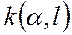- коэффициент, определяемый принятой доверительной вероятностью 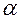и числом составляющих НСП 
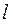(таблица 6,
Приложение 2)
Доверительную вероятность 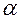для вычисления доверительной границы НСП принимают той же, что и при вычислении доверительной границы случайной погрешности результата измерения.
8. Вычислить доверительные границы погрешности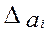 
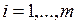результатов измерений каждой величины , ,…
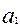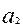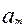
Если принять, что погрешность от пренебрежения систематической составляющей погрешности результата измерения не должна превышать 15%, то получим предельные отношения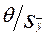 
. В зависимости о доверительной вероятности 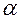, эти отношения равны
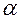0,90 0,95 0,99
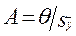1,2 1,1 1,1
Если пренебречь случайной составляющей, ориентируясь на ту же погрешность 15%, то
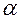0,90 0,95 0,99
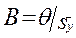3 4 7
Таким образом, если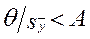 
, то с достаточной уверенностью можно пренебречь систематической, а если 
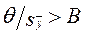- можно пренебречь случайной составляющей погрешности результата измерения.
Если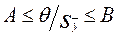 
при заданной доверительной вероятности 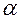, то границу погрешности результата измерения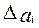 
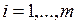(без учёта знака) можно вычислить по формуле
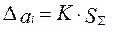, (14)
где
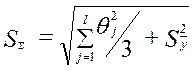, (15)
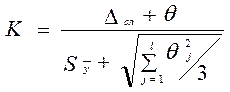, (16)
9. Вычислить значения частных производных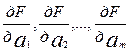 
при найденных ранее (см. п.5) оценках величин , ,… .
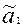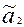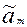10. Определить доверительную границу погрешности результата косвенного измерения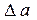 
по формуле
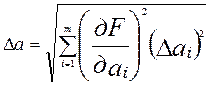, (17)
11. Определить относительную погрешность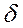 
результата косвенного измерения величины 
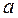по формуле
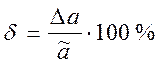, (18)
12. Результат косвенного измерения записывается в виде
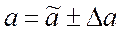
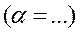(19)
Доверительную границу погрешности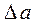 
, а также 
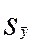и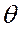 
следует выражать одной или двумя значащими цифрами. Две цифры оставляют при наиболее точных измерениях, а также в тех случаях, когда цифра старшего разряда числа, выражающего погрешность, меньше или равна трем. Отметим, что в промежуточных выкладках при расчете погрешностей нужно удерживать три-четыре значащих цифры. Результат косвенного измерения 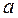необходимо округлять так, чтобы его значение оканчивалось цифрой того разряда, что и 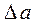после округления.
