Косвенным называется измерение, при котором значение искомой величины находят на основании известной зависимости, связывающей её с другими величинами, которые определяются прямыми измерениями. Обозначим искомую величину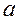 
, а величины, подвергаемые прямым измерениям 
, 
, …, 
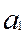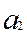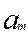Связь между нами задана в явном виде
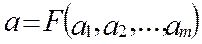, (3)
где F – известная функциональная зависимость
В данной расчётной работе предлагается один из способов обработки результатов наблюдений при косвенных измерениях.
Пусть при прямых измерениях для каждой из величин 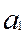, , 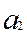…, 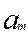получена группа результатов наблюдений. Процедура обработки состоит из следующих этапов.
Ⅰ. По результатам наблюдений при прямых измерениях величин 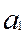, , 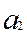…, 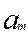рассчитываются выборочное среднее 
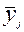и оценка среднего квадратического отклонения случайной погрешности 
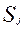для всех величин 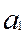, , 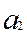…, 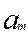подвергаемых прямым измерениям.
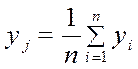(4)
j = 1,…,m
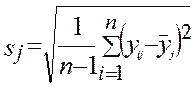, (5)
j = 1,…,m
где n – число результатов наблюдений
, 
, …, 
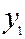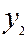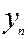- результаты полученные при прямых измерениях величины 
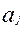(Приложение Ⅰ). В дальнейшем индекс j при величинах 
, 
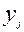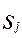и т. д. будем опускать.
2. Вычислить оценки среднего квадратического отклонения выборочного среднего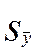 
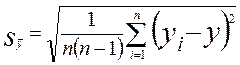(6)
3. Проверить гипотезу о том, что случайная погрешность подчиняется нормальному распределению.
В случае если 15 < n < 50 проверка осуществляется по двум критериям. Гипотеза о нормальности принимается только в том случае, если она принята, как по первому, так и по второму критериям.
