ѕолученные результаты измерений, как правило, подвергаютс€ статистической обработке, целью которой €вл€етс€ получение достоверных данных. ¬ основном статистическа€ обработка результатов измерений направлена на отсеивание грубых погрешностей измерени€ и определение закона распределени€ экспериментальных данных. —овокупность всех возможных наблюдений, которые могут быть сделаны при данном комплексе измерений, называетс€ генеральной совокупностью. ¬ыборкой называетс€ ограниченное число случайно отобранных наблюдений из генеральной совокупности.
ѕусть имеетс€ выборка экспериментальных данных x1, x2, x3, Е xi, Е, xN случайной величины ξ. —реднее значение этого р€да можно определить из выражени€
 .
.
¬ данном случае значение 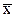 €вл€етс€ выборочным средним, так как оно вычислено по ограниченному числу измерений N. »спользу€
€вл€етс€ выборочным средним, так как оно вычислено по ограниченному числу измерений N. »спользу€ 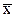 можно найти отклонение каждого результата от среднего
можно найти отклонение каждого результата от среднего
 .
.
¬еличину

называют оценкой дисперсии, она характеризует степень рассеивани€ случайной величины относительно своего выборочного среднего.
ќценка среднего квадратического отклонени€ может быть найдена по формуле 
¬ажными числовыми характеристиками €вл€ютс€ оценки моментов случайных величин. ќценка начального момента первого пор€дка:

ќценка начального момента второго пор€дка:

ќценка центрального момента k-го пор€дка находитс€ с помощью выражени€

ќценка первого центрального момента  =0. ќценка второго центрального момента €вл€етс€ оценкой дисперсии
=0. ќценка второго центрального момента €вл€етс€ оценкой дисперсии
 =
=  .
.
ќценка третьего центрального момента 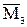 характеризует асимметрию распределени€ (случай, когда один спад крутой, а другой пологий). ƒл€ симметричных относительно центра распределений
характеризует асимметрию распределени€ (случай, когда один спад крутой, а другой пологий). ƒл€ симметричных относительно центра распределений 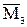
 . ќценка четвертого центрального момента
. ќценка четвертого центрального момента  характеризует прот€женность спадов распределени€, а его относительное значение
характеризует прот€женность спадов распределени€, а его относительное значение

называетс€ оценкой эксцесса распределени€.
ачество оценок характеризуетс€ состо€тельностью, несмещенностью, эффективностью. ќценка параметра называетс€ состо€тельной, если она по мере роста числа наблюдений стремитс€ к оцениваемому теоретическому значению параметра. ќценка параметра называетс€ несмещенной, если при любом числе наблюдений ее математическое ожидание точно равно значению оцениваемого параметра. ”довлетворение требовани€ несмещенности устран€ет систематическую погрешность, котора€ в случае состо€тельности оценки стремитс€ к нулю при числе наблюдений 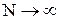 . ќценка параметра называетс€ эффективной, если среди прочих оценок того же параметра она обладает наименьшей дисперсией.
. ќценка параметра называетс€ эффективной, если среди прочих оценок того же параметра она обладает наименьшей дисперсией.
¬се сказанное выше относитс€ к равноточным измерени€м, т. е. к измерени€м одного происхождени€, выполненным одними инструментами и методами, которые содержат только случайную погрешность, подчин€ющуюс€ закону нормального распределени€.
ƒл€ исключени€ грубых погрешностей измерений (промахов) имеетс€ большое количество методик. Ќаиболее проста€ методика предполагает выполнение следующих пунктов:
1. »з измеренных значений выбирают то, которое имеет наибольшее отклонение от среднего (обозначим его как  );
);
|
|
|
2. ѕо формуле

вычисл€ют значение статистики τ дл€ выбранного значени€;
3. ѕо табл. 1.1 наход€т процентные точки распределени€ —тьюдента t(q, NЦ2), где, q Ц уровень значимости. ƒостаточно определить только два значени€ t(5 %, NЦ2) и t(0,1 %, NЦ2).
4. ƒл€ q=5 % и q=0,1 % вычисл€ют значени€

≈сли значени€ 
 , то результат измерени€ отсеивать нельз€. ѕри
, то результат измерени€ отсеивать нельз€. ѕри  результаты отсеивать можно, если в пользу этого имеютс€ другие соображени€. ƒл€
результаты отсеивать можно, если в пользу этого имеютс€ другие соображени€. ƒл€  измерени€ отсеиваютс€ всегда.
измерени€ отсеиваютс€ всегда.
“аблица 1.1
| NЦ2 | q | |||||||
| 10% | 5% | 2,5% | 1% | 0,5% | 0,25% | 0,1% | 0,05% | |
| t(p, NЦ2) | ||||||||
| 1,3104 | 1,6373 | 2,0423 | 2,4573 | 2,7500 | 3,0296 | 3,3852 | 3,6460 | |
| 1,3031 | 1,6869 | 2,0211 | 2,4233 | 2,7045 | 3,9712 | 3,3069 | 3,5510 | |
| 1,2931 | 1,6759 | 2,0089 | 2,4033 | 2,6778 | 2,9370 | 3,2614 | 3,1960 |

ƒл€ построени€ полигона и гистограммы на основе экспериментальных данных необходимо разбить диапазон изменени€ значений случайной величины на равные интервалы. оличество интервалов можно вычислить по следующему правилу:
 . (1.1)
. (1.1)
¬ данном случае K Ц целое число, получаемое из выражени€ (1.1) путем округлени€. –азность между максимальным и минимальным значени€ми измер€емой величины дел€т на K и получают длину интервала. ƒиапазон изменени€ значений случайной величины (разбитый на интервалы) откладываетс€ по оси абсцисс. ѕосле этого просматриваютс€ все измеренные значени€ и при чтении каждого результата метку (точку или черточку) став€т над тем интервалом, к которому относитс€ данное наблюдение. ѕосле чего осуществл€ют подсчет частостей.
ѕримеры кумул€тивной линии, гистограммы и полигона случайной величины приведены на рис. 1, 2 (кривые 1, 2, 3 соответственно). «десь в качестве измер€емой величины принимаетс€ сопротивление 56 резисторов. “очка с ординатой 0,089 кумул€тивной линии определ€етс€ как отношение числа измерений, попавших в данный класс к общему числу измерений. “.е. из числа резисторов, сопротивление которых соответствует первому классу (от 992 до 995 ќм) попали лишь 5 штук, тогда 5:56 = 0,089. —ледующа€ точка (0,321) определ€етс€ аналогичным образом, только к текущему результату добавл€етс€ предыдущий, т. е. сопротивлением от 995 до 998 ќм обладает 13 резисторов; 13:56 = 0,232; 0,232+0,089=0,321. јналогичным образом определ€ютс€ остальные точки.
 |
–ис. 1 –ис. 2
умул€тивна€ лини€ оценивает функцию распределени€ F(x) случайной величины. «начение функции распределени€ дл€ каждого x €вл€етс€ веро€тностью событи€, заключающегос€ в том, что случайна€ величина ξ принимает значени€ меньше x, т.е. F(x)=P(ξ<x).
√истограмма и полигон €вл€ютс€ оценками плотности веро€тности случайной величины. ≈сли плотность веро€тности случайной величины может быть хот€ бы приближенно описана кривой

то считаетс€, что данна€ случайна€ величина подчин€етс€ нормальному (√ауссову) закону распределени€.
ќбработка результатов измерени€ может быть существенно упрощена, если они подчин€ютс€ именно нормальному закону распределени€. ѕоэтому дл€ проверки нормальности распределени€ выработан р€д относительно простых критериев.
ƒл€ не очень больших выборок (N<120) можно примен€ть следующие рекомендации по проверке нормальности распределени€. ƒл€ этого необходимо вычислить среднее абсолютное отклонение (—јќ) по формуле

ƒл€ выборки, имеющей приближенно нормальный закон распределени€, должно быть справедливо выражение
|
|
|
 .
.
—уществуют и другие более точные методики определени€ нормальности распределени€, например,  Ц критерий, критерий олмогорова-—мирнова и др.
Ц критерий, критерий олмогорова-—мирнова и др.






