Методы оперативного аппаратного контроля

В качестве основного способа оперативного аппаратного контроля применяют контроль по модулю, контроль дублированием и контроль кодов.

Контроль дублированием. Контроль дублированием является наиболее простым способом аппаратного контроля. Суть метода состоит в том, что два одинаковых операционных устройства A и B работают синхронно при одинаковых исходных данных. В случае возникновения ошибки в одном из них, результаты на выходах A и B будут различаться, что фиксируется устройством сравнения.

Полнота контроля дублированием приближается к единице. Необнаружение ошибки может произойти по двум причинам:

а) если в устройствах А и В одновременно возникнут одинаковые ошибки;

б) если откажет устройство сравнения. Недостатком контроля дублированием является большое количество необходимой аппаратуры, а также то, что сравнение сигналов на выходе устройств позволяет обнаруживать ошибку не сразу, а только при появлении ошибочных результатов на выходе. Контроль дублированием применяется иногда для контроля самых ответственных и труднопроверяемых узлов и устройств ЭВМ, например, АЛУ.

Контроль по модулю. Наиболее широко в цифровых ЭВМ применяется контроль по модулю. Он относится к неполному контролю, основанному на группировании чисел в классы эквивалентности. Если в случае возникновения ошибки число переходит в другой класс эквивалентности, то такая ошибка обнаруживается простыми средствами. В противоположном случае ошибка не обнаруживается. В один и тот же класс эквивалентности входят числа, сравнимые по модулю. Пусть некоторое целое положительное число представлено в виде: A=aq+r_a,

где a, q и r_a - целые неотрицательные числа, а r_a может принимать значения от 0 до q-1.

Тогда число q называют модулем, а число r_a остатком А по модулю q.

В случае, когда числа А 1 и А 2 имеют одинаковые остатки ra1=ra2, то говорят, что А 1 и А 2 сравнимы по модулю q и записывают это условие следующим образом:

A 1 A 2 mod q или A 2≡ A 1 mod q

Поскольку число возможных значений r_a равно q, число классов эквивалентности, на которые разбивается множество неотрицательных чисел А, равно q. Отсюда следует общее свойство контроля по модулю: чем больше q, тем больше классов эквивалентности, тем меньше мощность каждого класса и тем меньше вероятность того, что в результате некоторой ошибки число останется в том же классе эквивалентности (и вследствие этого ошибка не обнаружится). Следовательно, большие значения q обеспечивают большую полноту контроля. Рекомендуется выбирать q=r±1, где r - основание системы счисления.

Таким образом, разбив все кодовые слова на классы, можно параллельно с основной операцией в контролируемом устройстве выполнять в контролирующем устройстве операцию над остатками. Результаты, полученные в этих устройствах, будут принадлежать к одному классу.

Контроль хранения или передачи числа по модулю q. Пусть число А передается по каналу связи или записывается на магнитный носитель М. Тогда при помощи преобразователя П 2 образуется остаток r _a, который передается дополнительным каналом связи (или записывается в дополнительное запоминающее устройство Мд). Пропускная способность дополнительного канала (или объем памяти дополнительного ЗУ) при этом значительно меньше тех же характеристик основного канала или ЗУ, т.к. разрядность остатка ra намного меньше разрядности числа А. Принятое (или считанное) число А*, которое, возможно, содержит искажения, подвергается также преобразованию П 1 с образованием остатка ra *, который затем сравнивается с остаток r _a. При несовпадении формируется соответствующий сигнал контроля

Числовой контроль арифметических операций. В основе числового контроля по модулю лежат следующие две теоремы:

1. Сумма чисел A_i(i=1,n) сравнима по модулю q с суммой остатков rai этих же чисел:

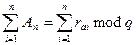
2. Произведение чисел A_i(i=1,n) сравнимо по модулю q с произведением остатков этих же чисел:

Контроль сложения чисел производится на основании теоремы 1.

Кроме суммы A *, которая после сложения чисел А 1 и А 2 в сумматоре S 1, воз -

можно, содержит ошибку, преобразователями П 1 и П 2 образуются остатки слагаемых ra1 и ra 2. После их суммирования в сумматоре S2 небольшой разрядности получается остаток суммы остатков r_a, который сравнивается с остатком ra *.

Контроль умножения чисел (рис.) производится аналогично контролю сложения, но с использованием теоремы 2. В приведенной схеме P1 - основное множительное устройство, Р 2 - вспомогательное множительное устройство небольшое разрядности. Множимое A₁ и множитель А₂ умножаются в основном множительном устройстве Р1, полученное произведение А_м* содержит, возможно, ошибку. Остаток ra * по модулю q результата сравнивается с остатком ra от произведения остатков ra1 и ra 2 множимого и множителя соответственно. Признаком ошибки служит несовпадение остатков. Перемножение остатков производится небольшим вспомогательным множительным устройством P2.

Контроль деления чисел. Этот контроль не может быть осуществлен по аналогии с контролем сложения и умножения, поскольку соответствующей теоремы нет. В основе контроля деления чисел лежит теорема 2.

При помощи преобразователей образуется остаток делимого и остаток от произведения частного и делителя, сравнение которых сравнивающим устройством дает сигнал об ошибке в случае несовпадения результатов. Кроме основного делительного устройства в структуре контроля участвует вспомогательное множительное устройство небольшой разрядности.

Контроль по модулю, хотя и экономичнее в смысле необходимых технических средств, чем полный контроль дублированием вычислений, все же нуждается в значительном количестве вспомогательных устройств.

Цифровой контроль по модулю основан на контроле по модулю суммы цифр, образующих число. Поскольку разрядность суммы цифр большого числа значительно меньше разрядности самого числа, операции вычисления остатка упрощаются, хотя дополнительно требуется операция для образования суммы цифр числа. Однако аналогов теорем 1 и 2 для суммы цифр операндов и результата сложения или умножения не существует, поэтому цифровой контроль непосредственно применим только для контроля операции хранения и передачи чисел.

Особенно просто цифровой контроль реализуется в случае двоичных чисел, когда модуль q=2. Такой контроль называется контролем по четности. При контроле по четности остаток суммы цифр равен нулю, либо единице в зависимости от четности числа единиц в исходном коде. В качестве остатка достаточно иметь один дополнительный разряд, называемый контрольным разрядом.

В двоичной системе счисления для обнаружения ошибок при передачи и хранении данных может быть использован цифровой контроль по модулю 2, как наиболее простой способ контроля, а для контроля арифметических операций - числовой контроль по модулю 3. Контроль по более высоким значениям модуля оправдан в особенно ответственных системах, где требуется эффективная защита от кратных ошибок.