2.1 Из предыдущего примера для статистического анализа возьмем каждый третий опыт, получим ограниченную выборку из 20-ти элементов следующего вида:
Таблица 7 – Ограниченная выборка измерения входного сопротивления транзисторов
| Номер измерения | 
| Номер измерения |
|
| 0,61 | 0,91 | ||
| 0,89 | 0,87 | ||
| 1,05 | 0,74 | ||
| 1,08 | 0,72 | ||
| 0,78 | 0,82 | ||
| 0,85 | 0,78 | ||
| 0,50 | 0,84 | ||
| 0,62 | 0,97 | ||
| 0,81 | 0,92 | ||
| 0,77 | 0,92 |
Составим группированный статистический ряд. Как и в предыдущей задаче, примем общее количество интервалов, равное шести. Максимальное значение исследуемого параметра равно 1,08, а минимальное – 0,5. Тогда размах варьирования по формуле (1) составит:
.
Определим ширину интервала по формуле (2):
.
Для удобства округлим значение интервала до сотых значений в большую сторону – примем равным 0,10.
Подсчитывая количество значений случайной величины, попавших в каждый разряд, относя значения, попавшие на границу между интервалами, к левому интервалу, а также деля на число опытов 
= 20, получаем следующий группированный статистический ряд частот, приведенный в таблице 8.
Таблица 8 – Группированный статистический ряд частот
| Интервалы | 0,50 ÷ 0,60 | 0,60 ÷ 0,70 | 0,70 ÷ 0,80 | 0,80 ÷ 0,90 | 0,90 ÷ 1,00 | 1,00 ÷ 1,10 |
| Середина интервала | 0,55 | 0,65 | 0,75 | 0,85 | 0,95 | 1,05 |
Частоты 
| 0,05 | 0,10 | 0,25 | 0,30 | 0,20 | 0,10 |
Для удобства проведения расчетов в данном примере, как и в предыдущем, воспользуемся методикой расчета моментов с использованием условных вариантов. Для нашего примера в качестве условного нуля в формуле (4) примем 
= 0,85. С целью удобства результаты расчета вспомогательных величин для определения условных начальных моментов сведем в таблицу 9.
Таблица 9 – Расчет вспомогательных параметров для определения условных начальных моментов
|
|  
| 
| 
|
| 0,55 0,65 0,75 0,85 0,95 1,05 | 0,05 0,10 0,25 0,30 0,20 0,10 | -3 -2 -1 | -0,15 -0,20 -0,25 0,20 0,20 | 0,45 0,40 0,25 0,20 0,40 |
| - | -0,20 | 1,70 |
Тогда условные начальные моменты первого и второго порядков по формулам (6) – (7) будут равны
;
;
С учетом формул (5) находим
;
.
2.2 Рассчитанная выше характеристика дисперсии является смещенной характеристикой. Для получения несмещенной оценки дисперсии эту характеристику следует умножить на поправочный коэффициент вида
. (17)
.
Тогда среднеквадратичное значение статистического параметра в данном случае будет равно
.
Окончательно значение статистического параметра для данной выборки записываем в следующем виде:
.
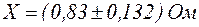2.3 Сравнивая результаты, полученные в данном примере, с результатами предыдущего примера, можно сделать вывод, что при анализе ограниченной выборки математическое ожидание параметра изменилось незначительно, а среднеквадратичное отклонение, характеризующее разброс этого параметра, при ограниченной выборке заметно больше.
