Задание № 2 Насос двойного действия
Вариант 4
Дано: H=210 мм, n1=90 об/мин, φ=90°, yB=0
1.1 Разбить механизм на структурные группы и определить степень подвижности
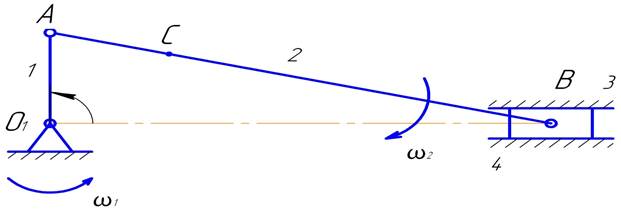
1- кривошип;
2- шатун;
3- ползун
4- стойка.
Определим степень подвижности механизма. Если звенья механизма абсолютно жесткие, то степень подвижности механизма совпадает с числом степеней свободы.
f = 3(n-1) – 2p1 –p2
n = 4; p1 = 4; p2 = 0, тогда f = 3(4-1) – 2*4 = 1.
1.2 Построить план положений звеньев механизма для 12-и значений угла поворота кривошипа. Определить крайние положения выходного звена и построить график перемещений в функции от угла поворота кривошипа.
2 lOA = H
lOA = H/2 = 210/2 = 105мм = 0, 105 м
lAB = lOA/0,25 = 105/0,25 = 420 мм = 0,420 м
lAC = 0,35 lAB = 0,35×420 = 147 мм = 0,147 м
План положений

График перемещений

1.3 Построить планы скоростей и ускорений (аналогов) для двух положений (одно из них крайнее, другое - заданное - φ=90°). Определить численные значения скоростей и ускорений и указать их направления на плане.
а) план скоростей для заданного положения φ = 90°

Угловая скорость первого звена: ω1 = 2πn1/60 = 2×3,14×90/60 = 9,42 рад/с
Скорость точки А: VA = ω1×OA = 9,42×0,075 = 0,71 м/с
Пользуясь планом скоростей, вычисляем масштабный коэффициент:
KV = VA/Va = 0,71/75 = 0,0095 (м/с) /мм
VВ = KV × Vb =0,0095×75 =0,71 м/с
VС = KV × Vс = 0,0095×75 = 0,71 м/с
VВА = 0 ( звено совершает мгновенно поступательное движение )
Va, Vb, Vс, Vba - измеряем эти значения на плане скоростей в мм
Угловая скорость второго звена: ω2 = VВА/ lAB = 0,86/0,3 = 2,96 рад/с
 б) план скоростей для крайнего положения φ = 0°
б) план скоростей для крайнего положения φ = 0°
VВ =0 м/с, VA = 0,71 м/с, VВА = VA = 0,71 м/с
ω2 = VВА/ lAB = 0,71/0,42 = 1,7 рад/с

в) план ускорений для заданного положения φ = 90°
ω1 = 9,42 рад/с = const, тогда  = 0 м/с2
= 0 м/с2
 = ω1× lOA =(9,42)2×0,075 =6,66 м/с2
= ω1× lOA =(9,42)2×0,075 =6,66 м/с2
 =
=  / lAB = 02/0,42 = 0 м/с2
/ lAB = 02/0,42 = 0 м/с2
Пользуясь планом ускорений, вычисляем масштабный коэффициент:
KW =  Wa = 6,66/60 = 0,111 (м/с2)/мм
Wa = 6,66/60 = 0,111 (м/с2)/мм
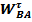 = KW × Wτ= 0,111 × 67,6 = 7,5 м/с2
= KW × Wτ= 0,111 × 67,6 = 7,5 м/с2

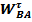 = ε2 × lAB ε2 =
= ε2 × lAB ε2 = 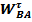 / lAB = 7,5/0,42 = 17,87 рад/с2
/ lAB = 7,5/0,42 = 17,87 рад/с2
WB =KW × Wb = 0,111×31,14 = 3,46 м/с2
WC =KW × Wc = 0,111×46,54 =5,17 м/с2
Wa, Wb, Wc, Wτ - измеряем эти значения на плане ускорений в мм
г) план ускорений для заданного положения φ = 0°

 =
=  / lAB = (0,71)2/0,42 = 1,2 м/с2
/ lAB = (0,71)2/0,42 = 1,2 м/с2

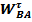 = 0 м/с2 ε2 = 0 рад/с2
= 0 м/с2 ε2 = 0 рад/с2
 = ω1× lOA =(9,42)2×0,105 =9,32 м/с2
= ω1× lOA =(9,42)2×0,105 =9,32 м/с2
Пользуясь планом ускорений, вычисляем масштабный коэффициент:
KW =  Wa = 9,32/70 = 0,133 (м/с2)/мм
Wa = 9,32/70 = 0,133 (м/с2)/мм
Wn =  /KW = 1,20/0,133 = 9,02 мм
/KW = 1,20/0,133 = 9,02 мм
WB =KW × Wb =0,1333×79 = 10,51 м/с2
 WC =KW × Wc =0,133×72,05 = 9,58 м/с2
WC =KW × Wc =0,133×72,05 = 9,58 м/с2
1.4 Составить выражение замкнутого векторного контура и спроектировать его на оси неподвижной системы координат, дважды продифференцировать уравнения по обобщенной координате и решить систему уравнений относительно неизвестных координат
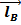 = xB×
= xB× 
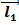 +
+ 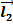 =
= 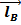 - условие замкнутости
- условие замкнутости
пример решения для заданного положения φ = 90°
l1 = lОА = 0,105 м, l2 = lАВ = 0,42 м

l1  + l2
+ l2 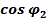 = xB
= xB
l1  + l2
+ l2  = 0
= 0
 = – l1
= – l1 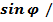 l2 = (– 0, 105×
l2 = (– 0, 105×  )/0,42 = – 0,25
)/0,42 = – 0,25
 =
= 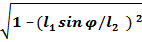 =
=  = 0,968
= 0,968
xB = l1  + l2
+ l2 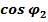 = 0,105×0+ 0,42×0,968 = 0,407 м
= 0,105×0+ 0,42×0,968 = 0,407 м
 – l1
– l1  – l2
– l2  =
= 
l1  + l2
+ l2 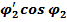 = 0
= 0
 = – l1
= – l1  l2
l2 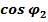 = – 0,105×0/0,42×0,968 = 0
= – 0,105×0/0,42×0,968 = 0
 = – l1
= – l1  – l2
– l2  = –0,105×1 –0,42×0×(– 0,25) = – 0,105 м
= –0,105×1 –0,42×0×(– 0,25) = – 0,105 м

–l1  – l2
– l2 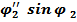 – l2
– l2  =
= 
– l1  + l2
+ l2 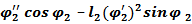 = 0
= 0
 = (
= (  + l1
+ l1  l2
l2 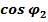 =
=
= (0,42×(0)2×(–0,25) + 0,105×1)/0,42×0,968 = 0,242
 = –l1
= –l1  – l2
– l2 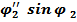 – l2
– l2  =
=
= –0,105×0 – 0,42×0,258×(–0,25)–0,42×(0)2×0,968 = 0,0254 м
ω1 = 2πn1/60 = 2×3,14×90/60 = 9,42 рад/с
ω2 =  × ω1 = 0×9,42 = 0 рад/с
× ω1 = 0×9,42 = 0 рад/с
 =
=  × ω1 = – 0,105 ×9,42 = – 0,99 м
× ω1 = – 0,105 ×9,42 = – 0,99 м
ε2 =  =
=  ×
×  = 0,242×(9,42)2 = 21,47 рад/с2
= 0,242×(9,42)2 = 21,47 рад/с2
 =
=  ×
×  = 0,0254×(9,42)2 = 2,25 м
= 0,0254×(9,42)2 = 2,25 м
1.5 Произвести численные расчеты линейных координат центров масс поршня и шатуна, а также его угол поворота в зависимости от угла поворота кривошипа с шагом 30°. рассчитать также численные значения аналогов скоростей и ускорений в 12-и положениях.
Результаты вычислений представить в виде таблицы. Для одного заданного положения привести пример расчета.
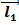 +
+  =
= 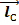 - условие замкнутости
- условие замкнутости
l1 = lОА = 0,105 м, l3 = lАС = 0,147 м
 l1
l1  + l3
+ l3 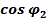 = xС
= xС
l1  + l3
+ l3  = yC
= yC
xС =0,105×0 + 0,147×0,968 =0,142 м
yC =0,105×1 + 0,147×(– 0,25) = 0,683 м

– l1  – l3
– l3  =
= 
l1  + l3
+ l3 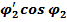 =
= 
 = –0,105×1 –0,147×0×(– 0,25) = - 0,105 м
= –0,105×1 –0,147×0×(– 0,25) = - 0,105 м
 = 0,105×0 + 0,147×0 ×0,968 = 0м
= 0,105×0 + 0,147×0 ×0,968 = 0м
 –l1
–l1  – l3
– l3 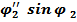 –
–  =
= 
– l1  + l3
+ l3  =
= 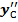
 = – 0,105×0 – 0,147×0,242×(– 0,25) –0,147×02×0,968 = 0,0089 м
= – 0,105×0 – 0,147×0,242×(– 0,25) –0,147×02×0,968 = 0,0089 м
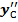 = – 0,105×1 + 0,147×0,242×0,968 –0,147×(0)2×(– 0,25) = – 0,0705 м
= – 0,105×1 + 0,147×0,242×0,968 –0,147×(0)2×(– 0,25) = – 0,0705 м
ω1 = 2πn1/60 = 2×3,14×90/60 = 9,42 рад/с
ω2 =  × ω1 = 0×9,42 = 0 рад/с
× ω1 = 0×9,42 = 0 рад/с
 =
=  × ω1 = – 0,105 ×9,42 = – 0,989 м
× ω1 = – 0,105 ×9,42 = – 0,989 м
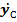 =
=  × ω1 = 0 ×9,42 = 0 м
× ω1 = 0 ×9,42 = 0 м
ε2 =  =
=  ×
×  = 0,242×(9,42)2 = 21,47 рад/с2
= 0,242×(9,42)2 = 21,47 рад/с2
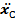 =
=  ×
×  = 0,0089 ×(9,64)2 = 0,83 м
= 0,0089 ×(9,64)2 = 0,83 м
 =
= 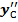 ×
×  = – 0,0705×(9,64)2 = – 6,55 м
= – 0,0705×(9,64)2 = – 6,55 м
1.6 Построить графики перемещений, аналогов скоростей и ускорений для поршня исполнительной машины.
Результаты вычислений представить в виде таблицы. Для одного заданного положения привести пример расчета.
График функции xB = xB(φ)

График функции  =
=  (φ)
(φ)

График функции  =
=  (φ)
(φ)

Задание 2 Насос двойного действия
Вариант 4
Дано:N=11 кВт, ng4=960 об/мин, nxx=1000 об/мин, z1=15, z2=28, m=5 мм, m1=11 кг, m2=24 кг, m3=55 кг, I1O=0,17 кгм2, n1=90 об/мин, H=210 мм, Dп=180 мм, φ=90°
2. Кинетостатический расчёт механизма
2.1 Используя заданную индикаторную диаграмму, определить силу полезного сопротивления в текущих положениях механизма и построить её график в функции от угла поворота кривошипа. Для одного из заданных положений входного звена записать силы инерции.
Дальнейшие расчёты приведены для заданного положения входного звена φ=30°
PC -сила полезного сопротивления
МДВ -момент движущих сил
ФX2 = – m2 ×  = – 24 × 0,83 = -19,92 Н
= – 24 × 0,83 = -19,92 Н
ФY2 = – m2 ×  –24 × (–6,55) = 157,2 Н
–24 × (–6,55) = 157,2 Н
ФX3 = – m3 × 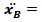 –55 × 2,25 = -123,75 Н
–55 × 2,25 = -123,75 Н
Вычисляемосевой момент инерции JC:
JC = 0,17× m2×  = 0,17×24×(0,42)2 = 0,72 кгм2
= 0,17×24×(0,42)2 = 0,72 кгм2
 –JC ×
–JC ×  = – 0,72×21,47 = – 15,46 Нм
= – 0,72×21,47 = – 15,46 Нм
| φ, град | ||||||||||||||
| РВ, 105 Па | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | |||||||
| РН, 105 Па | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 |

Для значений угла φ от 00 до 1800:
РС = (РВ–РН)×Sn = (6 –1)×105× 0,0254 = 12700 = 12,7 кН
Для значений угла φ от 1800 до 3600: РС = − 12,7 кН
График зависимости РС = РС(φ)

2.2 Выделить структурную группу механизма и входное звено. Составить уравнения статического равновесия, определить реакции в кинематических парах (внутренние - между звеньями, внешние - между подвижными звеньями и станины).
Реакции в кинематических парах:
R12 - сила, с которой первое звено действует на второе (реакция во вращательной паре)
R23 - реакция в ползуне В
RО1 - реакция в шарнире О1
RО3 - реакция в поступательной паре
Дальнейшие расчёты приведены для заданного положения входного звена






