Какая выдвигалась и проверялась гипотеза?

Гипотеза о нормальности закона распределения опытных данных:

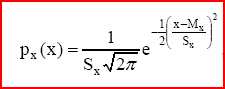
где е – основание натурального логарифма, px(x) – плотность распределения вероятности. Теоретически это утверждение обосновывается исходя из центральной предельной теоремы теории вероятностей, которая утверждает, что сумма многих независимых источников погрешностей с произвольными функциями распределения асимптотически имеет нормальное распределение, если только ни одна из этих погрешностей не является превалирующей.

При нормальном законе распределения погрешность =Sx в среднем может встречаться один раз на каждые 3 измерения, погрешность =2Sx – на каждые 22 измерения, а =3Sx – на каждые 370 измерений. В случае нормального закона распределения случайной величины за граничные значения погрешности принимают Мx3Sx.

Для проверки гипотезы о нормальности закона распределения случайной величины часто используют критерий согласия Xk 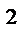.(Вопрос№4)

Определяют доверительный интервал (Xk ,0.5*q, Xk ,(1-0.5*q)) значений Xk в который может попадать мера расхождения.(Вопрос№4)

Если вычисленная по опытным данным мера расхождения Xk окажется в указанном интервале, то гипотеза о нормальности закона распределения опытных данных принимается, т.е. она правдоподобна и не противоречит опытным данным. Если Xk выходит за границы интервала, то гипотеза отвергается, как противоречащая опытным данным.