Матрицы параметров сложных четырехполюсников (последовательное, параллельное и каскадное соединения).
Тема № 2. Пассивные LC-фильтры
2.1. Теория фильтрующих четырехполюсников: классификация, расчет передаточных и входных функций нагруженных и ненагруженных пассивных фильтров типа К и m.
Электрический фильтр представляет собой 4-полюсник пропускающий без затухания(или с малыми затуханиями) сигнала, частоты которых лежат заданной полосе (полосе пропускания), и задерживающий или пропускающий с большим затуханием сигналы с частотами вне этой полосы (полосы задержки).
Граничную частоту между полосой пропускания и полосой задержки называют частотой среза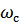 
. Различают фильтры: нижних частот с полосой пропускания 
, полосовой фильтр пропускающий частоты в полосе 
, заграждающий фильтр с полосой задержки 
.
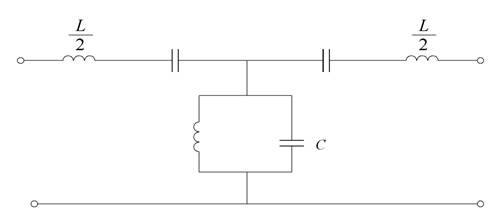
Наиболее простым получается расчет типовых звеньев Т- и П образного вида:
Расчёт А- параметров этих 4-полюсников уже производился.
В случае фильтров типа К продольная и поперечная ветви являются дуальными и произведение их сопротивлений 
является положительной вещественной константой.
Пусть каждое такое звено нагружено на его характеристическое сопротивление. Известно:
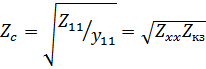
Для реактивных 4-полюсников:
Т.е. являются величинами противоположного знака.
Т.е. если знаки 
совпадают то cthγ имеет вещественное значение, а 
- мнимое.
Заметим, что 
Рассмотрим два возможных случая:
1. 
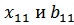имеют одинаковые знаки
cthγ- мнимый, следовательно:
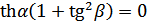
thα=0 >> α=0 при β≠0
т.е. получили полосу пропускания, где затухание α=0 и происходит лишь сдвиг сигналов по фазе:
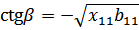
В полосе пропускания характеристическое сопротивление вещественно.
2. Знаки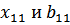 
различны
cthγ имеет вещественное значение:
tg β =0; β =0,π,2π……;
th α ≠0, α>0
Т.к. α>0, имеем полосу задержки в которой происходит затухание сигнала:
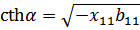
Фазовый сдвиг здесь не меняется имеет чисто мнимое значение(реактивное).
Расчет звена типа К состоит в том, что для заданных структур звеньев из реактивных элементов составляются выражения для 
и определяются их нули и полюсы.
Граничная частота полосы пропускания(частота среза) равняется тому полюсу, при котором происходит переход от совпадения к несовпадению знаков .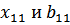
Пример:
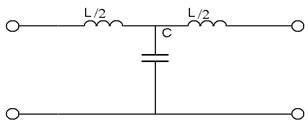Расчёт Т-образного фильтра нижних частот
Проводимость короткого замыкания:
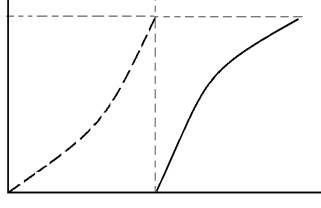
На рисунке показаны графики функций 
:
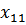
Частота среза равна полюсу-резонансной частоте контура, получающегося при коротком замыкании входа и выхода:
При 
знаки 
совпадают α=0-полоса пропускания.
Пр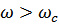и 
знаки различны, полоса задержки α>0.
Примерные графики затухания и фазы:
α,β π β
α
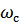ω
Напряжение на выходе отсекает от напряжения на входе, причем в полосе задержки- на π, напряжение на емкости сдвинуто на π относительно U1–вход.
Если соединить каскадно n звеньев то в n раз увеличится затухание в полосе задержки и фазовый угол:
1
s=jω
ω
Нагрузка фильтров обычно бывает активной, а 
-реактивное, т.е.согласование фильтра с нагрузкой в полосе частот выполнить не удается. Другим существенным недостатком фильтров типа К является малая крутизна нарастания затухания при переходе из полосы пропускания в полосу задержки.
Эти недостатки можно уменьшить если применить производные звенья типа m. Видоизменение состоит в замене поперечной емкости исходной схемы типа К (прототипа) последовательным резонансным контуром или продольной индуктивности прототипа параллельным контуром.
При m=1 – последовательное произвольное звено фильтра типа m переходит в звено прототипа К - типа.
Частота среза и характеристическое сопротивление звена m - типа и звена прототипа К - типа одинаковы.(эта частота соответствует резонансной частоте контура при коротком замыкании входа и выхода)
Поэтому звенья типа m могут каскадно соединяться со звеньями типа К.
Т-образное симметричное звено разобьём на два каскадно соединённых навстречу друг другу одинаковых Г-образных 4-полюсника.
где для П-образной схемы(расчет раньше) положить 
и учесть:
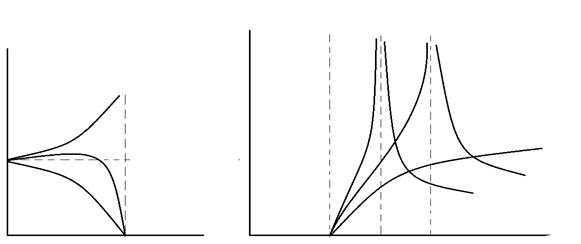
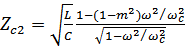
α 
m =0 m= 1
m =0.6
m =1 
0 ω 0 ω
Значение m≈0,6 является оптимальным, т.к. обеспечивает наибольшую равномерность (постоянство) в полосе пропускания. Это улучшает согласование фильтра с нагрузкой в полосе пропускания.
Наличие в поперечной ветви последовательного контура с резонансной частотой, превышающей частоту среза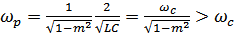 
даёт полюс затухания(бесконечное затухание).Это приводит к увеличению крутизны затухания вблизи границы полосы задержки. Чем меньше m, тем ближе 
.
В полосе задержки затухание фильтра типа m изменяется немонотонно, в отличие от фильтра типа К, что является недостатком фильтров типа m (не везде достаточное затухание).Для устранения недостатков(частичного) тех и других фильтров, m и К фильтры соединяют каскадно:
2.2 Фильтры верхних частот. Полосовые фильтры.
Фильтры других видов могут быть рассчитаны аналогично приведённому выше расчету фильтров нижних частот. Но они могут быть получены также путём пересчета данных исходного фильтра нижних частот с помощью преобразования частоты.
Например, для сведения фильтра нижних частот(прототипа) к искомому фильтру верхних частот используют преобразования:
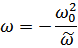
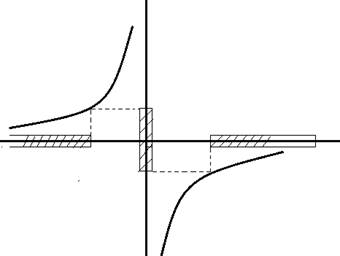ω
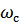
Схему цепи и значения элементов получим путём замены индуктивного элемента ёмкостным,
а ёмкостного элемента- индуктивным.
Получается схема звена ВЧ:
Для получения частотной характеристики полосового фильтра используют преобразования:
При 
и 
полоса пропускания полосового фильтра.
=> 
Определим значения элементов и схему полосового фильтра
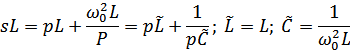
то есть индуктивный элемент преобразуется в последовательный колебательный контур.
Преобразование емкостного элемента:
Дает параллельный колебательный контур.
Для получения заградительного фильтра применим обратное преобразование к (*).
