Тема № 1. Основы теории четырехполюсников и многополюсников
Многополюсники и цепи с многополюсными элементами.
В теории четырехполюсников исследуются общие свойства цепи по отношению к внешним выводам независимо от конкретного вида схемы.
Для этого устанавливаются соотношения между двумя парами напряжений и токов: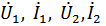 
входа и выхода, которые полностью характеризуют поведение цепи относительно выводов.
Из этих 4 величин лишь две любых являются независимыми. Уравнения четырехполюсников выражают остальные две величины (неизвестные) через известные. Число таких уравнений равно
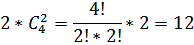
или 6 систем уравнений по 2 в каждой системе.
Коэффициенты этих уравнений называют параметрами 4х-полюсников.
Основные уравнения теории четырехполюсников и их первичные параметры.
1.1 Уравнения и параметры четырехполюсников.
а) система Y-параметров
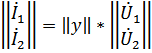
или
Входные проводимости:
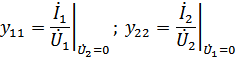
Передаточные проводимости:
В цепях, удовлетворяющих принципу взаимности: 
.
Поведение таких четырехполюсников определяется тремя параметрами. Если дополнительно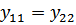 
, то получим симметричный четырехполюсник, имеющий лишь два независимых параметра.
б) системы Z – параметров
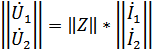
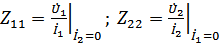- входные сопротивления;
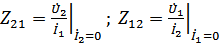- передаточные сопротивления.
В обратных цепях: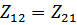 
(три независимых параметра).
Дополнительно 
– симметричный четырехполюсник с двумя независимыми параметрами. Параметры сопротивлений являются дуальными параметрами проводимостей.
в) система A – параметров (параметры передачи).
Разрешая систему (*) относительно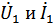 
:
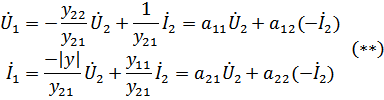
где параметры передачи:
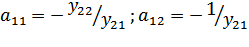
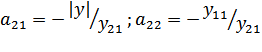
где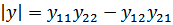 
Таким образом, параметры одной системы четырехполюсника могут быть выражены через параметры другой системы того же четырехполюсника.
Для обратимых четырехполюсников:
,
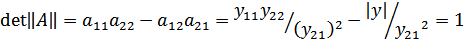так как 
для симметричных четырехполюсников: =>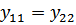 
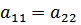
Смысл параметров A определяется опытами холостого хода и короткого замыкания на зажимах четырехполюсника:
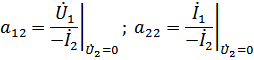
В режиме холостого хода на выходе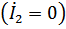 
напряжение и ток на входе:
; 
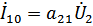
а в режиме короткого замыкания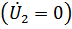 
напряжение и ток на входе:
Систему (**) можно рассматривать как наложение режимов холостого хода и короткого замыкания:
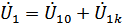
Систему (**)
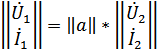
можно преобразовать к виду
где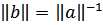 
, то есть
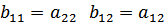
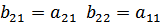
г) смешанные системы параметров
h-параметры:
= 
= 
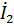Причем
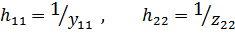
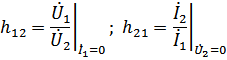
Для обратных цепей: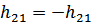 
g-параметры:
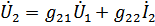
Причем
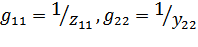
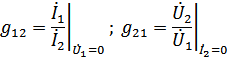
Для обратных цепей: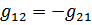 
; и для симметричных четырехполюсников:
Два четырехполюсника называют эквивалентными, если их параметры одинаковы.
