Вектор Умова-Пойнтинга —характеризует направление распространения мощности электромагнитной волны. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:
Волновое сопротивление среды
Волновые уравнения
Движение электромагнитного возмущения, изображенного на рисунке, можно точно описать с помощью волновых уравнений, легко выводимых из уравнений Максвелла.
Для гармонических полей справедлива форма записи
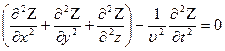решением является сферическая волна
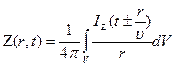
Таким образом, любое возмущение состояния электромагнитного поля приводит к появлению сферических волн 
, 
, 
, 
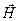, которые разбегаются со скоростью 
во всех направлениях от источника.
Замедляющие структуры
Гофра
Высота ребра- 
Структура гофры состоит из идеально проводящей подложки и набора идеально проводящих пластин. Решетка частая – ее период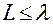 
Необходимо получить условия, при которых данная система являлась замедляющей структурой. Как видно из рисунка основным параметром структуры является высота ребра, поэтому все выкладки будут направлены на то, чтобы получить выражение определяющие параметр , при котором структура будет замедляющей.
Из условия, что решетка частая следует, что между ребрами существует кабельная волна, ее особенность в том, что 
может быть представлена гармонической функцией, удовлетворяющей граничным условиям на поверхности идеального металла.
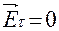
Далее необходимо получить значения 
, поскольку для хорошо проводящих поверхностей существуют граничные условия Леонтовича – связывают тангенсальные составляющие электрических и магнитных полей, через волновые сопротивления поверхностей.
найдем через уравнение Максвелла: 
Вычеркиваем строки содержащие 
, получим:
Теперь получим отношения 
к 
при значении 
(движение к 0 с отрицательной стороны)
, 
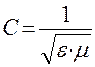, подставим эти равенства в выражение стоящее выше
Рассмотрим волну при 
(т.е. над гофрой). Над гофрой, как замедляющей структурой бежит волна в направлении 
убывая по экспоненте: 
Для неоднородных плоских волн все поперечные компоненты составляющих и 
определяются через продольные компоненты:
Приравнивая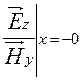 
и 
получаем уравнение: 
Использую соотношение 
, получим 
Гофра считается узкополосной замедляющей структурой. В каждой области допустимых значений эффект замедления возрастает с ростом .
