3.6.1-1
Полная система уравнений Максвелла для электромагнитного поля имеет вид:
 Следующая система уравнений:
Следующая система уравнений:
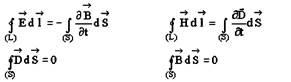 справедлива для …
справедлива для …
| 1. в отсутствие заряженных тел 2. в отсутствие заряженных тел и токов проводимости* 3. при наличии заряженных тел и токов проводимости 4. в отсутствие токов проводимости |
Рассмотрим уравнения Максвелла.
1-е уравнение – закон полного тока: циркуляция напряженности магнитного поля по произвольному замкнутому контуру определяется током проводимости и быстротой изменения потока электрической индукции через площадь, охваченную данным контуром.
 2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
 3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
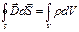 4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
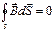 Таким образом, видно, что в заданных уравнениях
Таким образом, видно, что в заданных уравнениях  и и  , а, следовательно, они справедливы для переменного электромагнитного поля в отсутствие заряженных тел и токов проводимости. Ответ: 2 , а, следовательно, они справедливы для переменного электромагнитного поля в отсутствие заряженных тел и токов проводимости. Ответ: 2
|
3.6.1-2
Полная система уравнений Максвелла для электромагнитного поля имеет вид:
 Следующая система уравнений:
Следующая система уравнений:
 справедлива для …
справедлива для …
| 1: стационарного электрического и магнитного полей* 2: переменного электромагнитного поля при наличии заряженных тел и токов проводимости 3: переменного электромагнитного поля в отсутствие заряженных тел 4: переменного электромагнитного поля в отсутствие токов проводимости |
Рассмотрим уравнения Максвелла.
1-е уравнение – закон полного тока: циркуляция напряженности магнитного поля по произвольному замкнутому контуру определяется током проводимости и быстротой изменения потока электрической индукции через площадь, охваченную данным контуром.
 2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
 3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
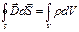 4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
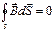 В заданных уравнениях
В заданных уравнениях  . Это означает, что поля стационарные, т. е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного поля – только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля. Ответ: 1 . Это означает, что поля стационарные, т. е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного поля – только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля. Ответ: 1
|
3.6.1-3
Полная система уравнений Максвелла для электромагнитного поля имеет вид:
 Следующая система уравнений:
Следующая система уравнений:
 справедлива для переменного электромагнитного поля …
справедлива для переменного электромагнитного поля …
| 1: в отсутствие заряженных тел* 2: в отсутствие заряженных тел и токов проводимости 3: при наличии заряженных тел и токов проводимости 4: отсутствие токов проводимости |
Рассмотрим уравнения Максвелла.
1-е уравнение – закон полного тока: циркуляция напряженности магнитного поля по произвольному замкнутому контуру определяется током проводимости и быстротой изменения потока электрической индукции через площадь, охваченную данным контуром.
 2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
 3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
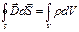 4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
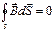 В заданных уравнениях
В заданных уравнениях  . Это означает, что заряженные тела отсутствуют. Ответ: 1 . Это означает, что заряженные тела отсутствуют. Ответ: 1
|
3.6.1-4
Полная система уравнений Максвелла для электромагнитного поля имеет вид:
 Следующая система уравнений:
Следующая система уравнений:
 справедлива для переменного электромагнитного поля …
справедлива для переменного электромагнитного поля …
| 1: в отсутствие токов проводимости* 2: в отсутствие заряженных тел и токов проводимости 3: при наличии заряженных тел и токов проводимости 4: в отсутствие заряженных тел |
Рассмотрим уравнения Максвелла.
1-е уравнение – закон полного тока: циркуляция напряженности магнитного поля по произвольному замкнутому контуру определяется током проводимости и быстротой изменения потока электрической индукции через площадь, охваченную данным контуром.
 2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
 3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
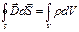 4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
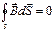 В заданных уравнениях
В заданных уравнениях  , что означает отсутствие токов проводимости. Ответ: 1 , что означает отсутствие токов проводимости. Ответ: 1
|
3.6.1-5
Полная система уравнений Максвелла для электромагнитного поля имеет вид:



 Следующая система уравнений:
Следующая система уравнений:



 справедлива для переменного электромагнитного поля …
справедлива для переменного электромагнитного поля …
| 1: при наличии токов проводимости и в отсутствии заряженных тел 2: в отсутствие заряженных тел и токов проводимости 3 при наличии заряженных тел и в отсутствии токов проводимости* 4: при наличии заряженных тел и токов проводимости |
Рассмотрим уравнения Максвелла.
1-е уравнение – закон полного тока: циркуляция напряженности магнитного поля по произвольному замкнутому контуру определяется током проводимости и быстротой изменения потока электрической индукции через площадь, охваченную данным контуром.
 2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
 3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
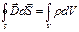 4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
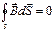 В заданных уравнениях
В заданных уравнениях  , что означает наличие заряженных тел и в отсутствие токов проводимости. Ответ: 3 , что означает наличие заряженных тел и в отсутствие токов проводимости. Ответ: 3
|
3.6.1-6
Полная система уравнений Максвелла для электромагнитного поля имеет вид:

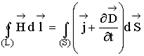

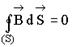 Следующая система уравнений:
Следующая система уравнений:



 справедлива для переменного электромагнитного поля …
справедлива для переменного электромагнитного поля …
| 1: в отсутствие заряженных тел и токов проводимости 2: при наличии заряженных тел и в отсутствии токов проводимости 3 при наличии токов проводимости и в отсутствии заряженных тел* 4: при наличии заряженных тел и токов проводимости |
Рассмотрим уравнения Максвелла.
1-е уравнение – закон полного тока: циркуляция напряженности магнитного поля по произвольному замкнутому контуру определяется током проводимости и быстротой изменения потока электрической индукции через площадь, охваченную данным контуром.
 2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
 3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
 4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
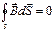 В заданных уравнениях
В заданных уравнениях  , что означает наличие токов проводимости и в отсутствие заряженных тел. Ответ: 3 , что означает наличие токов проводимости и в отсутствие заряженных тел. Ответ: 3
|
3.6.2-1
Следующая система уравнений Максвелла для электромагнитного поля



 справедлива переменного электромагнитного поля …
справедлива переменного электромагнитного поля …
| 1. в отсутствие заряженных тел 2. в отсутствие заряженных тел и токов проводимости* 3. в отсутствие токов проводимости 4. при наличии заряженных тел и токов проводимости |
Рассмотрим уравнения Максвелла.
1-е уравнение – закон полного тока: циркуляция напряженности магнитного поля по произвольному замкнутому контуру определяется током проводимости и быстротой изменения потока электрической индукции через площадь, охваченную данным контуром.
 2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
 3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
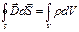 4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
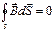 Таким образом, видно, что в заданных уравнениях
Таким образом, видно, что в заданных уравнениях  и и  , а, следовательно, они справедливы для переменного электромагнитного поля в отсутствие заряженных тел и токов проводимости. Ответ: 2 , а, следовательно, они справедливы для переменного электромагнитного поля в отсутствие заряженных тел и токов проводимости. Ответ: 2
|
3.6.2-2
Полная система уравнений Максвелла для электромагнитного поля имеет вид:

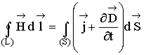
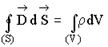
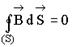 Эта система справедлива для переменного электромагнитного поля …
Эта система справедлива для переменного электромагнитного поля …
| 1: при наличии заряженных тел и токов проводимости* 2: в отсутствие заряженных тел и токов проводимости 3: в отсутствие заряженных тел 4: в отсутствие токов проводимости |
Рассмотрим уравнения Максвелла.
1-е уравнение – закон полного тока: циркуляция напряженности магнитного поля по произвольному замкнутому контуру определяется током проводимости и быстротой изменения потока электрической индукции через площадь, охваченную данным контуром.
 2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
 3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
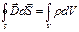 4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
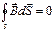 Представленные уравнения справедливы для переменного электромагнитного поля при наличии заряженных тел и токов проводимости. Ответ: 1
Представленные уравнения справедливы для переменного электромагнитного поля при наличии заряженных тел и токов проводимости. Ответ: 1
|
3.6.2-3
Следующая система уравнений Максвелла для электромагнитного поля:

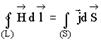
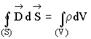
 справедлива для …
справедлива для …
| 1: стационарного электрического и магнитного полей* 2: переменного электромагнитного поля при наличии заряженных тел и токов проводимости 3: переменного электромагнитного поля в отсутствие заряженных тел 4: переменного электромагнитного поля в отсутствие токов проводимости |
1-е уравнение – закон полного тока: циркуляция напряженности магнитного поля по произвольному замкнутому контуру определяется током проводимости и быстротой изменения потока электрической индукции через площадь, охваченную данным контуром.
 2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
 3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
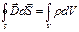 4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
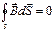 В представленной системе уравнений в отличие от исходной системы уравнений производные по времени от индукции электрического поля и индукции магнитного поля равны нулю – это означает, что данные величины не зависят от времени. Таким образом, в представленной система уравнений справедлива для стационарных электрических и магнитных полей при наличии заряженных тел и токов проводимости. Ответ: 1
В представленной системе уравнений в отличие от исходной системы уравнений производные по времени от индукции электрического поля и индукции магнитного поля равны нулю – это означает, что данные величины не зависят от времени. Таким образом, в представленной система уравнений справедлива для стационарных электрических и магнитных полей при наличии заряженных тел и токов проводимости. Ответ: 1
|
3.6.2-4
Следующая система уравнений Максвелла:



 справедлива для переменного электромагнитного поля …
справедлива для переменного электромагнитного поля …
| 1: в отсутствие заряженных тел* 2: в отсутствие заряженных тел и токов проводимости 3: при наличии заряженных тел и токов проводимости 4: отсутствие токов проводимости |
Рассмотрим уравнения Максвелла.
1-е уравнение – закон полного тока: циркуляция напряженности магнитного поля по произвольному замкнутому контуру определяется током проводимости и быстротой изменения потока электрической индукции через площадь, охваченную данным контуром.
 2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
 3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
 4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
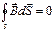 В заданных уравнениях
В заданных уравнениях  , что означает отсутствие заряженных тел. Ответ: 1 , что означает отсутствие заряженных тел. Ответ: 1
|
3.6.2-5
Следующая система уравнений Максвелла:



 справедлива для переменного электромагнитного поля …
справедлива для переменного электромагнитного поля …
| 1: в отсутствие токов проводимости* 2: в отсутствие заряженных тел и токов проводимости 3: при наличии заряженных тел и токов проводимости 4: в отсутствие заряженных тел |
Рассмотрим уравнения Максвелла.
1-е уравнение – закон полного тока: циркуляция напряженности магнитного поля по произвольному замкнутому контуру определяется током проводимости и быстротой изменения потока электрической индукции через площадь, охваченную данным контуром.
 2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
2-е уравнение – закон электромагнитной индукции: циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения магнитного потока через площадь, охваченную данным контуром, взятому с обратным знаком.
 3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
3-е уравнение – теорема Гаусса для электрического поля: поток индукции электрического поля через произвольную замкнутую поверхность равен заряду внутри этой поверхности.
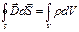 4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0.
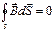 В заданных уравнениях
В заданных уравнениях  , что означает отсутствие токов проводимости. Ответ: 1 , что означает отсутствие токов проводимости. Ответ: 1
|
3.6.3-1
| Уравнение Максвелла, описывающее отсутствие в природе магнитных зарядов, имеет вид … | 1:  *
2: *
2:  3:
3:  4:
4: 
|
4-е уравнение – теорема Гаусса для магнитного поля: поток индукции магнитного поля через произвольную замкнутую поверхность равен заряду 0. Данная теорема определяет отсутствие в природе магнитных зарядов.
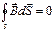 . Ответ: 1 . Ответ: 1
|






