Составитель: Панкратов Ю.M.
Санкт-Петербург
Лабораторная работа №3
Целью работы является знание приемов отделения корней и численных методов приближенного решения алгебраических и трансцендентных уравнений.
1. Теоретические сведения
1.1. Отделение корней
Отыскание приближенных значений корней уравнений состоит из двух этапов – отделение корней и их уточнение с заданной степенью точности. Отделение корней представляет процедуру по разбиению всей области числовой оси на интервалы, в каждом из которых содержится один корень, и ее можно выполнить двумя способами – графическим и аналитическим. При графическом методе строят график функции, который позволяет легко находить отрезки, заключающие в себе только один корень. При аналитическом методе корни уравнения f(x)=0 можно отделить, используя следующую теорему:
Если функция f(x) непрерывна на отрезке [a,b] и принимает на концах отрезка значения разных знаков, а производная f’(x) сохраняет постоянный знак внутри отрезка, то внутри отрезка существует корень уравнения f(x)=0 и при том единственный.
Поскольку MathCAD позволяет достаточно просто построить график любой функции, то воспользуемся графическим методом, учитывая утверждения этой теоремы. Тогда отделение корней можно выполнить в следующем порядке:
1. Построить график функции f(x) в интервале, охватывающем все корни уравнения. Если этот интервал очень большой, то можно построить несколько графиков для каждого корня в увеличенном масштабе.
2. Под этим графиком в том же масштабе по оси абсцисс построить график первой производной f’(x).
3. Проанализировав эти графики с учетом вышеизложенной теоремы, уже можно, хотя и довольно грубо, указать границы интервалов [ai ,bi] для каждого i-го корня.
4. Более наглядно и точнее эту задачу можно решить, если построить еще один совмещенный график сигналов функции f(x) и ее первой производной f’(x). Например, сигнал значений функции f(x) принять равным 1.5, сигнал значений первой производной f’(x) принять равным 1 (чтобы не сливались при совпадении). Функции этих сигналов можно вычислить как
sf(x):=1.5 sign(f(x) - для функции f(x);
sf1(x):= sign(f1(x) - для первой производной f’(x), где f1(x) - первая производная f’(x).
При выборе границ интервалов [ai ,bi] для каждого корня надо учитывать, что они не должны совпадать или даже близко приближаться к точкам экстремумов функции f(x) или, что то же самое, к значениям x, при которых f’(x)=0. В этих областях для некоторых методов уточнения корней сходимость итерационных процессов в выбранном интервале [ai ,bi] не гарантирована.
1.2. Уточнение корней
В работе рассматриваются только четыре метода уточнения корней. Считаем, что абсциссы xa и xb границ интервала [ai ,bi], содержащего единственный корень, известны.
1.2.1. Метод половинного деления
Алгоритм метода:
1. Вычисляют абсциссу xc средней точки, делящей отрезок [ai ,bi] пополам (Рис.1.) xc = (xa+xb)/2;
2. Вычисляют значение функции f(xc) в средней точке;
3. 
Если f(xc)× f(xb) > 0, то отрезок [xc, xb] можно отбросить, как не содержащий корня, выполнив присвоение xb= xc (на рис.1 функция для этого случая показана сплошной линией). Таким образом, правая граница будет смещена влево на половину интервала. В противном случае отбрасывают отрезок [xa, xc] с помощью присвоения xa= xc (на рис.1 функция для этого случая показана штриховой линией).
4. Если |xb - xa| > e, то цикл повторяют, начиная с п.1, в противном случае считают, что найденное значение и есть корень уравнения этого интервала, вычисленный с точностью e.
Достоинства метода: простота алгоритма, высокая надежность отыскания корня. Недостаток – большое количество шагов итераций.
1.2.2. Метод хорд
Алгоритм метода:
1. Одну из граничных точек принимают за неподвижную точку xc. Обычно это точка, в которой знак функции совпадает со знаком второй производной, т.е. f(xc)× f’’(xc) > 0. Тогда вторую граничную точку принимают за начальное приближение x0 (Рис.2.);
2. Каждое следующее значение абсциссы xi+1 вычисляют как точку пересечения хорды, соединяющей неподвижную точку xc и крайнюю текущую точку кривой xi , с осью абсцисс по формуле: 
3. Если |xi+1 – xi | > e, то цикл повторяют, начиная с п.2, в противном случае считают, что найденное значение и есть корень уравнения этого интервала, вычисленный с точностью e.
Метод обладает теми же достоинствами и недостатками, как и предыдущий.
1.2.3. Метод касательных (метод Ньютона)
Алгоритм метода:
1. За начальное приближение x0 принимают граничную точку, в которой знак функции совпадает со знаком второй производной, т.е. f(x0)×f’’(x0)> 0 (Рис.3.);
2. Каждое следующее значение абсциссы xi+1 вычисляют как точку пересечения касательной, проведенной в текущей точкой кривой xi , с осью абсцисс по формуле: 
3. Если |xi+1 – xi | > e, то цикл повторяют, начиная с п.2, в противном случае считают, что найденное значение и есть корень уравнения этого интервала, вычисленный с точностью e.
Достоинства метода: простота алгоритма, высокая скорость сходимости. Недостатки: необходимость отыскания первой производной в аналитической форме, ненадежность отыскания корня в указанном диапазоне. На рис.3 показано, что в случае проведения касательной в точке b, она может пересечься с осью x в точке c, лежащей за пределами выбранного интервала [a,b], и корень может быть найден совсем в другом интервале.
1.2.4. Метод итераций
Алгоритм метода:
1. Исходное уравнение f(x)=0 преобразуют к виду: x=F(x) (1)
2. Левая часть этого уравнения представляет уравнение прямой линии, проходящей через начало координат под углом в 45° к оси x. Абсцисса пересечения этой прямой с функцией F(x)и представляет корень уравнения f(x)=0(Рис.4.).
3. Задают начальное приближение x0 и вычисляют значение функции F(x0) (см.рис.4а). Из (1) следует, что его можно принять за первое приближение x1: x1=F(x0).
4. Вычислив функцию F(x1), принимают это значение за второе приближение x2=F(x1) и так далее. В общем случае для (i+1)-й итерации можно записать:
xi+1=F(xi ). (2)
5. Итерации повторяют, пока выполняется условие |xi+1 – xi | > e.
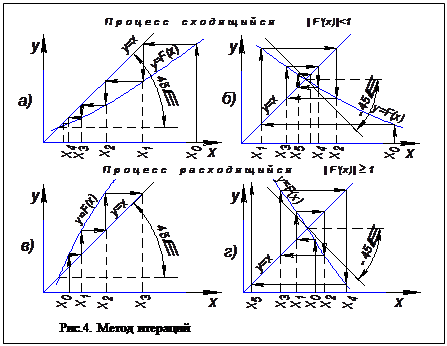
Геометрическая интерпретация метода показана на рис.4, причем на рис.4а) и 4б) процесс сходится к корню уравнения f(x)=0, а на рис.4в) и 4г) – расходится, хотя начальное приближение x0 и выбрано для них ближе к корню. Из рис.4а) можно заметить, что угол наклона касательной к любой точке кривой y=F(x) не превышает 45° к оси x, т.е. F’(x)<1. Из рис.4б) следует, что для этого случая F’(x)>-1. На рис.4в) и 4г) это условие не соблюдается и итерационный процесс на них расходится от корня уравнения. Отсюда следует, что для обеспечения сходимости итерационного процесса должно соблюдаться условие:
|F’(x)|<1 (3)
Для обеспечения сходимости процесса любых функций, можно воспользоваться одним из следующих вариантов:
Вариант 1.
· Исходное уравнение f(x)=0 умножают на постоянный коэффициент C: C×f(x)=0 (4)
· Прибавляют к обеим частям аргумент x: x=x+C×f(x) (5)
· Из (3) следует, что для обеспечения сходимости процесса должно быть выполнено условие:
|[ x+C×f(x)]’|<1, или после преобразования
|1+C×f’(x)|<1. (6)
· Поскольку левая часть неравенства является модулем, то возможны два решения:
1-е решение: 1+C×f’(x)<1, или C×f’(x)<0; 2-е решение: -1-C×f’(x)<1, или C×f’(x)>-2.
Оба этих решения можно записать как: -2<C×f’(x)<0.
· Отсюда отыскивают границы диапазона значений C, при которых сходимость процесса будет обеспечена. В зависимости от знака f’(x) левую и правую границу диапазона коэффициента C вычисляют из следующих неравенств:
при f’(x)>0 
при f’(x)<0 
(7)
· Поскольку при поиске корня известны только абсциссы интервала [ai ,bi], в котором находится корень, то необходимо вычислить границы диапазона C при значениях xa и xb и принять C как среднее арифметическое между ними.
Вариант 2.
· Из рис.4а) и 4б) следует, что наибольшая скорость сходимости итерационного процесса будет при горизонтальном расположении кривой функции y=F(x), т.е. когда ее первая производная будет равна нулю. Тогда неравенство (6) можно записать в виде равенства 1+C×f’(x)=0, откуда 
(8)
· В этом варианте также необходимо найти C для граничных точек интервала [ai ,bi], но уже по формуле (8):
(9)
· Окончательное значение C для всего интервала можно принять как среднее арифметическое
C=(Ca+Cb) /2. (10)
Интересно отметить, что подстановка формулы (8) в (5) приводит к формуле Ньютона.
Для обоих вариантов начальное приближение можно принимать как x0=(xa+xb) /2.
Метод обладает теми же достоинствами и недостатками, что и предыдущий, к тому же добавляется необходимость вычислять коэффициент C.
1.3. Использование встроенных функций
Для проверки выполненных решений можно воспользоваться встроенной функцией root, которая в MathCAD’е 2001 имеет уже две формы:
· root(f(x),x)
· root(f(x),x,a,b)
где f(x) - скалярная функция вида f(x)=0;
x - скалярная переменная, относительно которой решается уравнение;
a,b - границы интервала, внутри которого отыскивается корень.
Первая форма требует предварительного присвоения переменной x начального значения, вблизи которого будет производиться поиск корня методом секущих, не рассматриваемом в этой работе. Для второй формы, использующей методы Риддера или Брента, достаточно указания интервала [a,b], внутри которого заведомо находится корень.
Точность вычисления функцией root определяется системной переменной TOL, которая по умолчанию равна 0.001. Ее можно изменить на вкладке Математика/Параметры…/Переменные.
2. Задание
Задание состоит из функции f(x)=0, для которой требуется отыскать все корни с точностью e=0.001.
Варианты задания:
| № | Функция f(x)=0 | № | Функция f(x)=0 | № | Функция f(x)=0 | № | Функция f(x)=0 |
| 1. | 0.5x+2sin(x)-2=0 | 9. | 0.01x3+cos(x)-0.2=0 | 17. | 15cos(x-0.1)+0.4x3=0 | 25. | x4+(10-x)3+x-600=0 |
| 2. | x3+(8-x)2-60=0 | 10. | 3cos(x-0.5)+0.4x2=0 | 18. | sin(x)+0.2x2=0 | 26. | sin(x)+cos(2x)+0.8x-3=0 |
| 3. | 0.2x2+3sin(x)+1=0 | 11. | 0.01x4-2(x-5)2-25x=0 | 19. | (12-sin(x))2-x2-134=0 | 27. | 0.04x3+2(x-4)2-2x-5=0 |
| 4. | x3-15(x-5)+1=0 | 12. | 5(x-4)4+10(x-5)3+x2=0 | 20. | x4-x3+x2-5=0 | 28. | 4sin(x)-x2+0.2=0 |
| 5. | 20cos(x)+x3-10=0 | 13. | sin(x2)+5(x+8)-2=0 | 21. | x4+x3-x2-5=0 | 29. | sin(x2)+x+2=0 |
| 6. | 20cos2(x)+x3-10=0 | 14. | 8sin(x)+2x2-4=0 | 22. | 8cos(x)+x2-4=0 | 30. | 24cos(x-1)+sin(x)+10x-25=0 |
| 7. | 2cos(x-5)+(x-8)2-2=0 | 15. | 40cos(x-5)+(x-8)3-2=0 | 23. | 5cos(x)+(x-4)2-3=0 | 31. | 10cos(x)+5sin(x)+4x-10=0 |
| 8. | 10sin(x)+4x-15=0 | 16. | 2sin(x)-x+0.2=0 | 24. | 5cos(x)+(x-8)2-7=0 | 32. | 8cos(x2)+(x-2)3+5x-3=0 |
Отчет по работе должен включать:
2.1. Отделение корней, для чего необходимо построить графики функции f(x), ее первой производной f’(x) и график сигналов.
2.2. Уточнение корней методами половинного деления, хорд, касательных и итераций.
2.3. Проверку результатов с помощью встроенной функции root.
2.4. Выводы
3. Пример выполнения задания
4. Литература
1. Бахвалов Н.С. Численные методы. – М., Наука,1975. –632 c.
2. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. – М., Наука,1976. –304 с.
3. Волков Е.А. Численные методы: Учебное пособие для вузов. – 2-е изд. – М., Наука, 1987.
4. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. – М., Наука,1972.
5. Турчак Л.И., Плотников П.В. Основы численных методов: Учеб. пособие.– 2-ое изд., перераб. и доп. -М.: ФИЗМАТЛИТ, 2002. –304 c.
6. Исаков В.Н. Элементы численных методов. – М., Издательский центр «Академия»,2003. –192 c.
