Решение систем линейных уравнений
Векторные и матричные операторы и функции системы MatCAD позволяют решать широкий круг задач линейной алгебры. К примеру, если задана матрица А и вектор В для системы линейных уравнений в матричной форме А*Х:=В, то вектор решения можно получить из очевидного выражения
Х:=А-1*В.
Поскольку решение систем линейных уравнений довольно распространенная задача, то для этого в MatCAD, начиная с шестой версии введена встроенная функция lsolve(A,B), которая возвращает вектор Х для системы линейных уравнений А*Х=В при заданной матрице коэффициентов А и векторе свободных членов В. Если уравнений n, размерность вектора В должна быть n, а размер матрицы А – n* n.
Приведем пример решения системы линейных уравнений (обратите внимание, что решаемая система имеет матрицу с комплексными коэффициентами):
| А:= | 0.24 | -0.08 | |
| 0.09 | -0.15 | ||
| 0.04 | -0.08 |
Матрица коэффициентов системы
| В:= | |
Вектор свободных членов
Х:=А-1В Решение системы
| Х= | 1.909 |
| 3.195 | |
| 5.0450 |
Результаты решения
| Х1= | 1.909 |
| 3.195 | |
| 5.0450 |
Решение с применением функции lsolve:
Х1:=lsolve(A,B)
Поиск корня нелинейного уравнения с помощью функции
Root
Многие уравнения, например трансцендентные, и системы из них не имеют аналитических решений. Однако они могут решаться численными методами с заданной погрешностью(не более значения, заданного системной переменной TOL). Для простейших уравнений вида F(x)=0 решение находится с помощью функции
root (выражение, Имя_переменной)
Эта функция возвращает значение переменной, при котором выражение дает 0. Функция реализует вычисления итерационным методом, причем можно задать начальное значение переменной. Это особенно полезно, если возможно несколько решений. Тогда выбор решения определяется выбором начального значения переменной. Приведем пример решения кубического полинома.
Вычисление корней кубического полинома
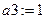
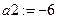
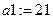
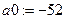Коэффициенты полинома
F(x):=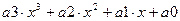 
Задание полинома
