Средняя арифметическая является наиболее распространенной среди средних величин. Ее применяют в тех случаях, когда даны отдельные объекты с индивидуальными значениями признаков, выраженными абсолютными показателями. Среднюю арифметическую определяют как отношение суммы индивидуальных значений признаков к их количеству.
Различают среднюю арифметическую простую и взвешенную. Среднюю арифметическую простую применяют в случае, если индивидуальные значения признака в совокупности встречаются по одному разу, а взвешенную - если индивидуальные значения признака представлены несколькими объектами.
Среднюю арифметическую простую определяют по формуле:
,
где 
-средняя;
х -варианты;
n -число вариант.
Формула средней арифметической взвешенной имеет вид:
,
где f -частота вариант.
Средняя арифметическая величина, описанная выше, является обобщающей характеристикой совокупности по тому или иному признаку. Вспомогательными характеристиками являются, так называемые, структурные средние, к которым относятся мода, медиана и др. Наиболее употребляемыми являются мода и медиана.
Мода - это величина, которая встречается в совокупности наиболее часто, то есть признак с наибольшей частотой. Этот показатель используется в тех случаях, когда требуется охарактеризовать наиболее часто встречающуюся величину признака (наиболее распространенный размер животноводческих ферм на сельскохозяйственных предприятиях, преобладающие цены на сельскохозяйственную продукцию и т. п.).
Медианой называется величина, делящая численность упорядоченного вариационного ряда (расположенного в порядке возрастания или убывания признака) на две равные части. Медиана характеризует количественную границу значений изменяющегося признака, которыми обладает половина единиц совокупности. Например, если медианное значение удоя коровы составляет 4735 кг, то это означает, что половина коров имеет удой молока ниже 4735 кг и половина коров выше.
В дискретном вариационном ряду модой является признак с наибольшей частотой. Медианой является признак с номером, который находят путем деления суммы частот упорядоченного вариационного ряда на два и добавления 0,5.
В интервальном вариационном ряду моду находят по формуле:
,
где Мо - мода;
хМо -нижняя граница модального интервала;
hМо - величина модального интервала;
fМо - частота модального интервала;
fМо-1 - частота интервала, предшествующего модальному;
fМо+1 - частота интервала, следующего за модальным.
Модальным интервалом является интервал с наибольшей частотой.
Формула расчета медианы в интервальном вариационном ряду:
,
где Ме - медиана;
хМе - нижняя граница медианного интервала;
hМе - величина медианного интервала;
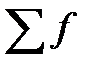- сумма частот;
sМе−1 - сумма частот, накопленных в интервалах, предшествующих медианному;
fМе - частота медианного интервала.
Медианным интервалом является интервал, накопленная частота которого равна или превышает половину суммы частот.
Для измерения вариации применяют различные показатели, из которых основными являются размах вариации (лимит), среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Дисперсию рассчитывают как среднюю арифметическую квадратов отклонений вариант от средней арифметической:
простая 
;
взвешенная 
,
где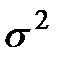 
- дисперсия.
Среднее квадратическое отклонение равно корню квадратному из дисперсии:
простое 
;
взвешенное 
,
где 
- среднее квадратическое отклонение
Коэффициент вариации представляет собой процентное отношение среднего квадратического отклонения к средней арифметической величине:
,
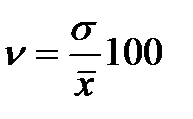где 
-коэффициент вариации.
Коэффициент асимметрии для выборки рассчитывается по формуле:
где As – коэффициент асимметрии;
– момент третьего порядка;
– выборочное среднее квадратическое отклонение;
n – число вариант.
Показатель эксцесса для выборки рассчитывается по формуле:
или 
,
где 
– эксцесс;
– момент четвертого порядка.
3.2.1. Вариант «Настриг шерсти»
Таблица 4. Расчет суммарной величины настрига шерсти
| № п/п | Настриг шерсти, кг (y) |
| 4,1 | |
| 4,2 | |
| 4,2 | |
| 4,2 | |
| 4,3 | |
| 4,3 | |
| 4,4 | |
| 4,5 | |
| 4,5 | |
| 4,7 | |
| 4,8 | |
| 4,8 | |
| 4,8 | |
| 4,8 | |
| 4,9 | |
| 4,9 | |
| 4,9 | |
| 4,9 | |
| 5,1 | |
| 5,1 | |
| 5,2 | |
| 5,2 | |
| 5,4 | |
| Сумма: | 117,2 |
Расчет средней арифметической: 
кг.
Таким образом, среднегодовой настриг шерсти за год составляет 4,688 кг.
Для расчета моды и медианы необходим анализ Таблицы 2, рассчитанной выше:
| Номер интервала | Группа овец по величине веса настрига, Yi | Число овец | Середина интервала | Накопленная частота | |
| нижняя граница | верхняя граница | fi | Y i’ | fi’ | |
| 4,24 | 4,12 | ||||
| 4,24 | 4,48 | 4,36 | |||
| 4,48 | 4,72 | 4,6 | |||
| 4,72 | 4,96 | 4,84 | |||
| 4,96 | 5,2 | 5,08 | |||
| 5,2 | 5,44 | 5,32 | |||
| Итого: | х | х |
Моду и медиану рассчитывают по формулам для интервального вариационного ряда.
Для нахождения моды необходимо определить модальный интервал. Таким будет интервал 4,72 – 4,96 с наибольшей частотой (число овец) 8. Отсюда мода равна:
кг.
Для нахождения медианы надо определить медианный интервал. Половина суммы частот равна 12,5 (число овец 25: 2). Следовательно, согласно накопленным частотам медианным интервалом будет также 4,72 - 4,96 (так как 12,5 < 19). Медиана равна:
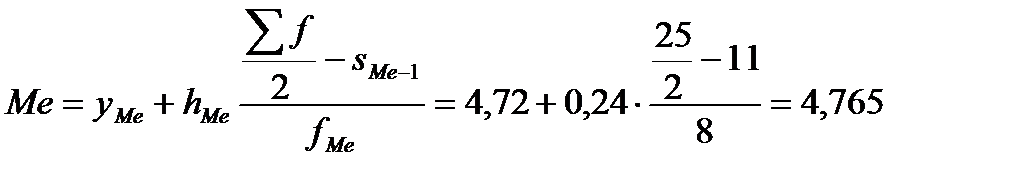кг.
Для дальнейших расчетов – показателей вариации, – необходимо выполнить ряд операций с исходными данными, результаты которых представлены в Таблице 5.
Таблица 5. Обработка ряда для вычисления показателей вариации
| № п/п | Настриг шерсти, кг (y) | Yi-Yср | (Yi-Yср)2 | ((Yi-Yср)/s)3 | ((Yi-Yср)/s)4 |
| -0,688 | 0,4733 | -5,4098 | 9,4967 | ||
| 4,1 | -0,588 | 0,3457 | -3,3771 | 5,0667 | |
| 4,2 | -0,488 | 0,2381 | -1,9305 | 2,4038 | |
| 4,2 | -0,488 | 0,2381 | -1,9305 | 2,4038 | |
| 4,2 | -0,488 | 0,2381 | -1,9305 | 2,4038 | |
| 4,3 | -0,388 | 0,1505 | -0,9703 | 0,9606 | |
| 4,3 | -0,388 | 0,1505 | -0,9703 | 0,9606 | |
| 4,4 | -0,288 | 0,0829 | -0,3968 | 0,2916 | |
| 4,5 | -0,188 | 0,0353 | -0,1104 | 0,0529 | |
| 4,5 | -0,188 | 0,0353 | -0,1104 | 0,0529 | |
| 4,7 | 0,012 | 0,0001 | 0,0000 | 0,0000 | |
| 4,8 | 0,112 | 0,0125 | 0,0233 | 0,0067 | |
| 4,8 | 0,112 | 0,0125 | 0,0233 | 0,0067 | |
| 4,8 | 0,112 | 0,0125 | 0,0233 | 0,0067 | |
| 4,8 | 0,112 | 0,0125 | 0,0233 | 0,0067 | |
| 4,9 | 0,212 | 0,0449 | 0,1583 | 0,0856 | |
| 4,9 | 0,212 | 0,0449 | 0,1583 | 0,0856 | |
| 4,9 | 0,212 | 0,0449 | 0,1583 | 0,0856 | |
| 4,9 | 0,212 | 0,0449 | 0,1583 | 0,0856 | |
| 0,312 | 0,0973 | 0,5045 | 0,4016 | ||
| 5,1 | 0,412 | 0,1697 | 1,1617 | 1,2213 | |
| 5,1 | 0,412 | 0,1697 | 1,1617 | 1,2213 | |
| 5,2 | 0,512 | 0,2621 | 2,2296 | 2,9127 | |
| 5,2 | 0,512 | 0,2621 | 2,2296 | 2,9127 | |
| 5,4 | 0,712 | 0,5069 | 5,9959 | 10,8928 | |
| Сумма: | 117,2 | -1,42109E-14 | 3,6864 | -3,1271 | 44,0249 |
Расчет дисперсии настрига шерсти: 
Среднее квадратическое отклонение настрига шерсти овец от средней:
кг.
Коэффициент вариации настрига шерсти овец: 
%.
Выборочная дисперсия настрига шерсти овец:
Выборочное среднее квадратическое отклонение настрига шерсти овец:
кг.
Асимметрия настрига шерсти:
Эксцесс настрига шерсти:
Полученные значения асимметрии и эксцесса показывают, что данное распределение имеет левостороннюю асимметрию и более высокую вариацию, чем при нормальном распределении.
3.2.2. Вариант «Длина волоса шерсти»
Таблица 6. Расчет суммарной величины длины волоса шерсти
| № п/п | Длина волоса шерсти, см (x) |
| 12,4 | |
| 13,8 | |
| 14,4 | |
| 14,5 | |
| 14,9 | |
| 15,4 | |
| 16,8 | |
| 16,8 | |
| 16,9 | |
| 17,3 | |
| 17,4 | |
| 17,4 | |
| 19,5 | |
| 20,6 | |
| 20,8 | |
| 21,2 | |
| 21,3 | |
| 21,3 | |
| 22,3 | |
| 22,5 | |
| 22,7 | |
| 24,2 | |
| Сумма: | 455,4 |
Расчет средней арифметической: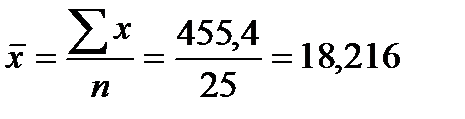 
см.
Таким образом, среднегодовая длина волоса шерсти за год составляет 18,216 см.
Для расчета моды и медианы необходим анализ Таблицы 3, рассчитанной выше:
| Номер интервала | Группа овец по величине волоса, Xi | Число овец | Середина интервала | Накопленная частота | |
| нижняя граница | верхняя граница | fi | Х i’ | fi’ | |
| 12,4 | 14,37 | 13,385 | |||
| 14,37 | 16,34 | 15,355 | |||
| 16,34 | 18,31 | 17,325 | |||
| 18,31 | 20,28 | 19,295 | |||
| 20,28 | 22,25 | 21,265 | |||
| 22,25 | 24,22 | 23,235 | |||
| Итого | х | х |
Моду и медиану рассчитывают по формулам для интервального вариационного ряда.
Для нахождения моды необходимо определить модальный интервал. Таким будет интервал 16,34 – 18,34 с наибольшей частотой (число овец) 7. Отсюда мода равна:
см.
Для нахождения медианы надо определить медианный интервал. Половина суммы частот равна 12,5 (число овец 25: 2). Следовательно, согласно накопленным частотам медианным интервалом будет также 16,34 - 18,31 (так как 12,5 < 14). Медиана равна:
см.
Для дальнейших расчетов – показателей вариации, – необходимо выполнить ряд операций с исходными данными, результаты которых представлены в Таблице 7.
Таблица 7. Обработка ряда для вычисления показателей вариации
| № п/п | Длина волоса шерсти, см (x) | Xi-Xср | (Xi-Xср)2 | ((Xi-Xср)/s)3 | ((Xi-Xср)/s)4 |
| 12,4 | -5,816 | 33,8259 | -5,1604 | 8,9176 | |
| -5,216 | 27,2067 | -3,7224 | 5,7690 | ||
| 13,8 | -4,416 | 19,5011 | -2,2589 | 2,9639 | |
| 14,4 | -3,816 | 14,5619 | -1,4576 | 1,6527 | |
| 14,5 | -3,716 | 13,8087 | -1,3460 | 1,4861 | |
| 14,9 | -3,316 | 10,9959 | -0,9564 | 0,9423 | |
| 15,4 | -2,816 | 7,9299 | -0,5857 | 0,4901 | |
| 16,8 | -1,416 | 2,0051 | -0,0745 | 0,0313 | |
| 16,8 | -1,416 | 2,0051 | -0,0745 | 0,0313 | |
| 16,9 | -1,316 | 1,7319 | -0,0598 | 0,0234 | |
| 17,3 | -0,916 | 0,8391 | -0,0202 | 0,0055 | |
| 17,4 | -0,816 | 0,6659 | -0,0143 | 0,0035 | |
| 17,4 | -0,816 | 0,6659 | -0,0143 | 0,0035 | |
| -0,216 | 0,0467 | -0,0003 | 0,0000 | ||
| 19,5 | 1,284 | 1,6487 | 0,0555 | 0,0212 | |
| 1,784 | 3,1827 | 0,1489 | 0,0789 | ||
| 20,6 | 2,384 | 5,6835 | 0,3554 | 0,2518 | |
| 20,8 | 2,584 | 6,6771 | 0,4526 | 0,3475 | |
| 21,2 | 2,984 | 8,9043 | 0,6970 | 0,6179 | |
| 21,3 | 3,084 | 9,5111 | 0,7694 | 0,7050 | |
| 21,3 | 3,084 | 9,5111 | 0,7694 | 0,7050 | |
| 22,3 | 4,084 | 16,6791 | 1,7868 | 2,1682 | |
| 22,5 | 4,284 | 18,3527 | 2,0624 | 2,6251 | |
| 22,7 | 4,484 | 20,1063 | 2,3649 | 3,1508 | |
| 24,2 | 5,984 | 35,8083 | 5,6207 | 9,9935 | |
| Сумма: | 455,4 | -3,19744E-14 | 271,8536 | -0,6623 | 42,9852 |
Расчет дисперсии настрига шерсти: 
Среднее квадратическое отклонение длины волоса шерсти овец от средней:
см.
Коэффициент вариации длины волоса шерсти овец:
%.
Выборочная дисперсия длины волоса шерсти овец:
Выборочное среднее квадратическое отклонение длины волоса шерсти овец:
см.
Асимметрия длины волоса шерсти:
Эксцесс длины волоса шерсти:
Полученные значения асимметрии и эксцесса показывают, что данное распределение имеет левостороннюю асимметрию и более высокую вариацию, чем при нормальном распределении.
