Диаграмма представляет собой совокупность точек, координаты которых равны значениям параметров X и Y.
Для удобства сведем значения параметров X и Y в таблицу:
| x | y | x | y | x | y | x | y |
| 118,5 | 80,3 | 123,8 | 84,7 | 81,6 | 121,5 | 83,2 | |
| 120,5 | 83,7 | 117,8 | 79,3 | 124,5 | 86,7 | 122,7 | 84,4 |
| 83,7 | 124,7 | 83,7 | 81,7 | 128,3 | 87,3 | ||
| 79,3 | 81,7 | 121,5 | 80,5 | 120,6 | 77,3 | ||
| 119,8 | 78,5 | 121,9 | 79,5 | 126,5 | 89,8 | 120,4 | 79,5 |
| 122,5 | 78,4 | 123,9 | 83,6 | 124,1 | 80,8 | ||
| 119,4 | 118,2 | 122,7 | 76,6 | 125,4 | 80,4 | ||
| 122,7 | 82,9 | 119,8 | 120,5 | 77,4 | 122,5 | 80,5 | |
| 115,8 | 77,5 | 122,8 | 81,2 | 78,5 | 118,5 | 85,2 | |
| 80,1 | 120,5 | 81,6 | 78,5 | 85,2 | |||
| 118,5 | 82,2 | 119,5 | 83,2 | 81,6 | |||
| 83,3 | 126,5 | 122,5 | 79,5 | ||||
| 118,5 | 82,5 | 121,9 | 124,5 | 78,5 | |||
| 81,6 | 79,5 | ||||||
| 121,2 | 79,5 | 123,5 | 80,5 | 118,5 | |||
| 121,5 | 83,5 | 80,5 | 121,2 | 78,8 | 80,3 | ||
| 122,4 | 81,6 | 119,2 | 79,6 | 120,9 | 84,1 | ||
| 121,3 | 80,2 | 124,4 | 86,7 | 120,4 | 79,5 | 119,3 | 78,5 |
| 121,3 | 80,2 | 121,3 | 79,6 | 119,3 | 122,5 | ||
| 121,5 | 119,1 | 81,8 | 118,6 | 78,2 | 119,3 | ||
| 117,5 | 74,5 | 122,5 | 81,7 | 78,6 | |||
| 124,5 | 84,9 | 118,8 | 82,6 | 118,3 | 80,7 | 83,7 | |
| 82,2 | 119,5 | 118,7 | 80,8 | 77,5 | |||
| 82,7 | 85,2 | 117,8 | 83,2 | 89,3 | |||
| 121,5 | 79,5 | 77,5 | 119,5 | 78,3 | 124,5 | 82,6 |
Нанесем точки на график.
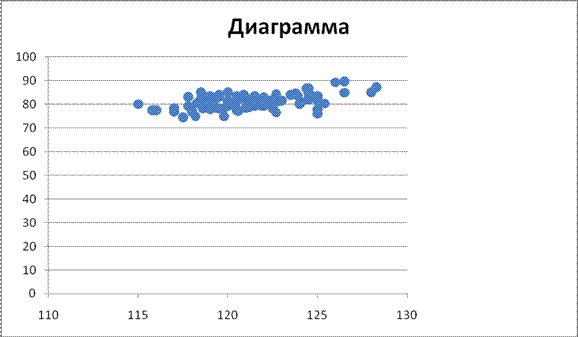
Вычислите коэффициент корреляции (он позволяет количественно определить силу линейной связи между x и y) по формуле:
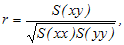Где
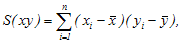
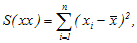
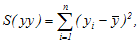
n – количество пар данных,
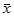– среднее арифметическое значение параметра x,
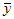– среднее арифметическое значение параметра y.
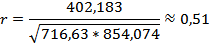
Исходя из этого, делаем вывод о существовании средней положительной корреляционной связи между X и Y.
