Таблица 1.7
118,5 120,5 125 120 119,8 122,5 119,4 122,7 115,8 115 118,5 125 118,5 125 121,2 121,5 122,4 121,3 121,5 117,5 124,5 121 121 121,5 123,8 117,8 124,7 121 121,9 123,9 118,2 119,8 122,8 120,5 119,5 119 121,9 120 123,5 119 119,2 124,4 121,3 119,1 117 118,8 119,5 120 118 120 124,5 122 121,5 126,5 124,1 122,7 120,5 117 121 123 126,5 124,5 118 119 121,2 122 120,4 119,3 118,6 122,5 118,3 118,7 117,8 119,5 121,5 122,7 128,3 120,6 120,4 125 125,4 122,5 118,5 128 125 122,5 121 122 118,5 124 120,9 119,3 122,5 119,3 121 119 116 126 124,5
Построение гистограммы.
Выстраиваем вариационный ряд, в котором Xmin= 115, Xmax= 128,3. Количество бинов гистограммы k= 7, а значит ширина бина r=1,5.
Определяем границы бинов (интервалы с числом наблюдений менее 5 присоединяем к соседним)
115; 118; 119,5; 121; 122,5; 124; 125,5; 128,3;
Частоты попадания измерений в интервалы, mi:
m1=10; m2=23; m3=19; m4=21; m5=9; m6=13; m7=5
Частости попадания измерений в интервалы, 
:
Плотность распределения,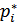 
:
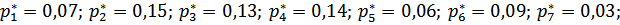
На основании чего строим гистограмму:
Проверка гипотезы о соответствии нормальному закону распределения по критерию Пирсона.
Для проверки гипотезы о соответствии экспериментального закона распределения теоретическому, необходимо, чтобы соблюдалось условие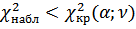 
, где 
По табличным значениям, принимая α =0,05,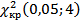 
= 9,48.
; где 
– теоретические частоты,
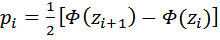– теоретические вероятности,
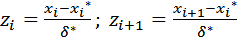- концы интервалов,
– середина каждого интервала,
δ* - выборочное среднеквадратичное (для каждого интервала).
Составим таблицу.
| 
| 
|
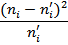
| 8,7 | 0,194 | |
| 18,81 | 0,001 | |
| 20,79 | 0,002 | |
| 8,73 | 0,008 | |
| 4,1 | 0,198 |
, а следовательно, гипотезу о том, что величина X распределена по закону F(x), можно считать правдоподобной, по крайней мере не противоречащей экспериментальным данным.
