3.133. Составить квадратное уравнение, имеющее корнями числа:
а) 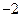 и
и  ; б)
; б) 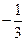 и
и 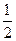 ;
;
в) 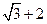 и
и 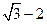 ; г)
; г) 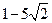 и
и 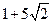 .
.
Ответы: а) 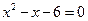 ; б)
; б) 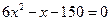 ;
;
в) 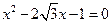 ; г)
; г) 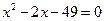 .
.
3.134. Не вычисляя корней уравнения 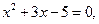 найти:
найти:
а) 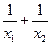 ; б)
; б) 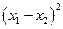 .
.
Ответы: а) 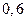 ; б)
; б) 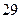 .
.
3.135. Не вычисляя корней уравнения 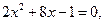 найти:
найти:
а) 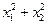 ; б)
; б) 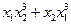 ; в)
; в) 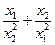 ; г)
; г) 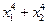 .
.
Ответы: а) 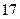 ; б)
; б) 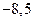 ; в)
; в) 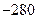 ; г)
; г) 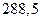 .
.
3.136. Не вычисляя корней уравнения 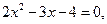 найти:
найти:
а) 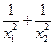 ; б)
; б) 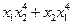 ; в)
; в) 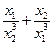 ; г)
; г) 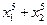 .
.
Ответы: а) 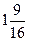 ; б)
; б) 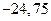 ; в)
; в) 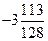 ; г)
; г) 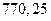 .
.
3.137. Не вычисляя корней уравнения 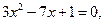 найти:
найти:
а) 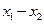 ; б)
; б) 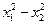 .
.
Ответы: а) 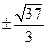 ; б)
; б) 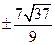 .
.
3.138. Пусть 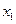 и
и 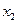 – корни квадратного уравнения
– корни квадратного уравнения 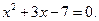 Не находя
Не находя 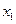 и
и 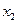 , составить квадратное уравнение, корнями которого являются числа:
, составить квадратное уравнение, корнями которого являются числа:
а) 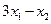 и
и 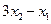 ; б)
; б) 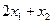 и
и 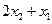 ;
;
в) 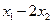 и
и 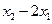 ; г)
; г) 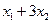 и
и 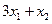 .
.
Ответы: а) 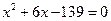 ; б)
; б) 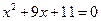 ;
;
в) 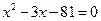 ; г)
; г) 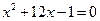 .
.
3.139. Пусть 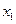 и
и 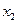 – корни квадратного уравнения
– корни квадратного уравнения 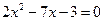 . Не находя
. Не находя 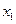 и
и 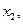 составить квадратное уравнение, корнями которого являются числа:
составить квадратное уравнение, корнями которого являются числа:
а) 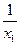 и
и 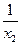 ; б)
; б) 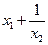 и
и 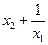 ; в)
; в) 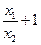 и
и 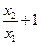 .
.
Ответы: а) 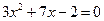 ; б)
; б) 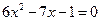 ;
;
в) 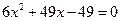 .
.
3.140. а) Известно, что квадратное уравнение 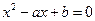 имеет два различных корня
имеет два различных корня 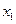 и
и 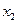 . Составить биквадратное уравнение, корнями которого являются числа
. Составить биквадратное уравнение, корнями которого являются числа 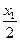 и
и 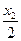 . (Коэффициенты биквадратного уравнения должны быть выражены через
. (Коэффициенты биквадратного уравнения должны быть выражены через 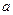 и
и 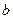 );
);
б) известно, что квадратное уравнение 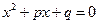 имеет два различных корня
имеет два различных корня 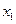 и
и 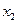 . Составить биквадратное уравнение, корнями которого являются числа
. Составить биквадратное уравнение, корнями которого являются числа 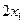 и
и 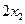 . (Коэффициенты биквадратного уравнения должны быть выражены через
. (Коэффициенты биквадратного уравнения должны быть выражены через 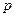 и
и 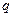 ).
).






