Основы машинных вычислений

Лабораторная работа №1

Цель: Формирование представления о способе хранения и представления информации в компьютере. Приобретение навыков перевода чисел в различные системы счисления и выполнение арифметических операций в двоичной системе счисления.

Теоретические сведения

 

Компьютер не понимает непосредственно команды на языке ассемблера, он понимает только машинные команды. Машинный язык состоит из чисел, которые интерпретируются процессором. Процессор обычно имеет встроенный интерпретатор, представляющий микропрограмму и преобразовывающий машинные команды непосредственно в управляющие сигналы.

Машинный язык включает примитивные операторы, которые могут исполнить простые арифметические действия или переместить данные. Система команд процессора состоит из машинных команд, которые он может исполнить. Машинный язык для семейства процессоров Intel в своей основе имеет систему команд процессора 8086, которые могут выполняться процессорами последующих модификаций. Такая концепция называется совместимостью сверху вниз.

Писать программы на машинном языке неудобно и утомительно, т.к. необходимо писать много чисел, сравнивать их коды. Гораздо удобнее использовать ассемблер, который преобразовывает коды, написанные на языке ассемблера в машинные коды. Для наглядности рассмотрим пример машинной команды, которая помещает число 5 в регистр процессора AL: 1011000000000101 Первые 8 битов- код операции, который предписывает поместить операнд в регистр AL. Вторые 8 битов являются операндом. На ассемблере данный пример выглядит так: mov AL, 5

Перед тем, как изучать язык ассемблера необходимо разобраться с представлением данных в компьютере, с системами счисления.

 

Двоичные числа

В компьютере информация представлена в двоичной системе счисления. Двоичные числа так же называют числами с основание 2, так как каждое число может принимать только два значения: 0 или 1. компьютеры сохраняют команды или данные как серию двоичных цифр, называемых битами. Двоичные цифры организованы группами по восемь цифр, называемых байтами. Байт может содержать простую машинную команду, символ или число. Два байта составляют слово, хотя количество байт в слове может быть различным в зависимости от конструкции компьютера. Используются так же двойные слова (32 бита) и учетверенные слова (64 бита).

В языках высокого уровня представление команд и данных имеет существенное различие, однако в компьютере они представлены как одинаковые наборы нулей и единиц. Таким образом, программисты, использующие язык ассемблера, должны разделять данные и команды.

 

Системы счисления

Для человека наиболее привычной системой счисления является десятичная. Для преобразования чисел из двоичной системы к более компактному виду используются восьмеричная и шестнадцатеричная системы счисления. Все перечисленные системы счисления являются позиционными т.е. обладающими следующим свойствам – количественное значение каждой цифры зависит от ее места (позиции) в числе.

Дадим краткую характеристику каждой системы счисления:

· Двоичная система – цифры 0 и 1.

Пример числа 100100110₍₂₎

· Восьмеричная система – цифры 0, 1, 2, 3, 4, 5, 6, 7.

Пример числа 235₍₈₎

· Десятичная система - цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Пример числа 453₍₁₀₎

· Шестнадцатеричная система – цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Пример числа 32A₍₁₆₎

 

Для перевода чисел из любой системы счисления в десятичную можно использовать правило позиционной системы счисления: (1)

 

P- основание системы счисления. Нижние индексы определяют местоположение цифры в числе (разряд): положительные значения индексов – для целой части числа (m разрядов), отрицательные значения - для дробной части (s разрядов).

Например, для перевода числа 235 используем правило позиционной системы 235₍₈₎=2*8²+3*8¹+5*8⁰=2*64+3*8+5*1=128+24+5=157₍₁₀₎

125,16₍₁₆₎=1*16²+2*16¹+5*16⁰+1*16^-1+6*16^-2=256+32+80+0,0625+0,0234 = 368,0859₍₁₀₎

101110,101₍₂₎=1*2⁵+0*2⁴+1*2³+1*2²+1*2¹+0*2⁰+1*2^-1+0*2^-2+

+1*2^-3=46,625₍₁₀₎

Практически перевод из двоичной системы в десятичную можно легко выполнить, надписав над каждым разрядом соответствующий ему вес и сложив затем произведения значений соответствующих цифр на их веса.

Например, двоичное число 0100001₍₂₎ равно 65₍₁₀₎.
Действительно, 64 * 1 + 1 * 1 = 65.

Вес
Цифра

 

Таким образом, для перевода числа из позиционной системы счисления с любым основанием в десятичную систему счисления можно воспользоваться выражением (1). Обратный перевод из десятичной системы счисления в систему счисления с другим основанием непосредственно по формуле (1) для человека весьма затруднителен, поскольку все арифметические действия, предусмотренные этой формулой, следует выполнять в той системе счисления, в которую число переводится. Обратный перевод выполняется значительно проще, если предварительно преобразовать отдельно целую и дробную части выражения (1) к виду

 

 

Алгоритм перевода числа из десятичной системы счисления в систему счисления с основанием Р, основанный на этих выражениях, позволяет оперировать числами в той системе счисления, из которой число переводится, и может быть сформулирован следующим образом: при переводе смешанного числа следует переводить, его целую и дробную части отдельно.

1. Для перевода целой части числа ее, а затем целые части получающихся частных от деления, следует последовательно делить на основание Р до тех пор, пока очередная целая часть частного не окажется равной 0. Остатки от деления, записанные последовательно справа налево, образуют целую часть числа в системе счисления с основанием Р.

2. Для перевода дробной части числа ее, а затем дробные части получающихся произведений, следует последовательно умножать на основание Р до тех пор, пока очередная дробная часть произведения не окажется равной 0 или не будет достигнута нужная точность дроби. Целые части произведений, записанные после запятой последовательно слева направо, образуют дробную часть числа в системе счисления с основанием Р.

Пример перевода смешанного числа из десятичной системы в двоичную систему 46,625₍₁₀₎

 

		0,625 1,250 0,500 1,000

 

 

 

 

 

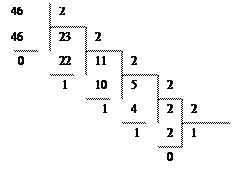Окончательно получаем 46,625₍₁₀₎=101110,101₍₂₎

 

Таб. 1.1

Для перевода из двоичной системы счисления в восьмеричную и шестнадцатеричную систему счисления (и наоборот), удобно использовать таблицу перевода, приведенную ниже:

 

 

IV	III	II	I	8-я или 16-я
				A
				B
				C
				D
				E
				F

 

Для перевода чисел из 8-й системы в двоичную достаточно использовать 3 двоичных разряда, а для перевода из 16-й системы достаточно использовать 4 двоичных разряда.

Например, переведем 1364₍₈₎ в двоичную систему счисления, используя таблицу.
1364₍₈₎=001 011 110 100₍₂₎

Переведем A15₍₁₆₎ в двоичную систему счисления.
A15₍₁₆₎=1010 0001 0101₍₂₎

Перевод из двоичной системы в 8-ю и 16-ю выполняется аналогично по таблице, надо только иметь ввиду, что можно с левой стороны числа добавлять нулей столько сколько нужно.
Например, перевести двоичное число 10010100111₍₂₎ в 8-ю систему счисления.
10010100111₍₂₎=010 010 100 111₍₂₎=2247₍₈₎

Перевести это же число в 16-ю систему счисления
10010100111₍₂₎=0100 1010 0111₍₂₎=4A7₍₁₆₎

 

Представление числовой информации на компьютере

 

В вычислительных машинах применяются три формы представления двоичных чисел:

· естественная форма, или форма с фиксированной запятой (точкой);

· нормальная форма, или форма с плавающей запятой (точкой);

· двоично – десятичное представление.

В форме представления с фиксированной запятой все числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.

Например: в десятичной системе счисления имеется 5 разрядов в целой части числа (до запятой) и 5 разрядов в дробной части числа (после запятой); числа, записанные в такую разрядную сетку, имеют вид:

+00721,35500; +00000,000328: -10301,20260.

Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел и поэтому чаще всего не приемлема при вычислениях. Диапазон значащих чисел N в системе счисления с основанием Р при наличии m разрядов в целой части и 5 разрядов в дробной части числа (без учета знака числа) будет таким:

 

Например, при Р= 2, m= 10 и s = 6 числа изменяются в диапазоне 0,015 < М< 1024.

Если в результате операции получится число, выходящее за допустимые пределы, произойдет переполнение разрядной сетки, и дальнейшие вычисления теряют смысл. В современных компьютерах естественная форма представления используется как вспомогательная и только для целых чисел.

В форме представления с плавающей запятой каждое число изображается в виде двух групп цифр. Первая группа цифр называется мантиссой, вторая — порядком, причем абсолютная величина мантиссы должна быть меньше 1, а порядок должен быть целым числом. В общем виде число в форме с плавающей запятой может быть представлено так:

 

где М — мантисса числа (|М| < 1); r — порядок числа (целое число); Р — основание системы счисления.

Например, приведенные ранее числа в нормальной форме запишутся следующим образом: +0,721355 * 10³; +0,328 *10^-3; -0,103012026 *10⁵.

Нормальная форма представления имеет огромный диапазон отображения чисел и является основной в современных компьютерах. Так, диапазон значащих чисел в системе счисления с основанием Р при наличии m разрядов у мантиссы и s разрядов у порядка (без учета знаковых разрядов порядка и мантиссы) будет:

 

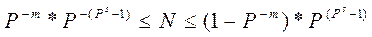Например при Р = 2, m=22 и 5=10 диапазон чисел простирается при­мерно от 10^-300 до 10³⁰⁰. Для сравнения: количество секунд, которые прошли с мо­мента образования планеты Земля, составляет всего 10¹⁸.

Следует заметить, что все числа с плавающей запятой хранятся в машине в так называемом нормализованном виде. Нормализованным называют такое число, в старшем разряде мантиссы которого стоит единица. У нормализованных дво­ичных чисел, следовательно,.

 

 

Третья форма предоставления двоичных чисел – двоично-десятичная. Ее появление объясняется следующим. При обработке больших массивов десятичных чисел (например, больших экономических документов) приходится тратить существенное время на перевод этих чисел из десятичной системы счисления в двоичную для последующей обработки и обратно – для вывода результатов. Каждый такой перевод требует выполнения двух –четырех десятков машинных команд. С включением в состав отдельных ЭВМ специальных функциональных блоков или спецпроцессоров десятичной арифметики появляется возможность обрабатывать десятичные числа напрямую, без их преобразования, что сокращает время вычислений. При этом каждая цифра десятичного числа представляется двоичной тетрадой. Например, А₍₁₀₎=3759, А_(2-10) =0011 0111 0101 1001. Положение десятичной точки (запятой), отделяющей целую часть от дробной, обычно заранее фиксируется. Значение знака числа отмечается кодом, отличным от кодов цифр. Например, «+» имеет значение тетрады «1100», а «-»- «1101».

 

Алгебраическое представление двоичных чисел

 

Знак числа обычно кодируется двоичной цифрой, при этом код 0 означает знак + (плюс), код 1 — знак - (минус). Числа со знаком используют старший разряд в качестве знакового. Таким образом, если используется число без знака, то для 8-разрядного числа используются все 8 бит, то максимальное число 255. Для 8- разрядного числа со знаком используются 7 бит, а восьмой знаковый, максимальное число будет 127. Для алгебраического представления чисел, то есть для представления чисел с учетом их знака, в вычислительных машинах используются специальные коды:

прямой код числа;

обратный код числа;

дополнительный код числа.

При этом два последних кода позволяют заменить неудобную для компьютера операцию вычитания на операцию сложения с отрицательным числом. Дополнительный код обеспечивает более быстрое выполнение операций, поэтому в компьютере применяется чаще именно он.

1.Прямой код числа N,обозначим [N]пр.

Пусть N=a1, a2, a3,... am, тогда:

При N>0, [N]пр.=0, a1, a2, a3,... am;

При N<0, [N]пр.=1, a1, a2, a3,... am;

При N=0 имеет место неоднозначность [0]пр.=0, 0 …= 1, 0 …

Если при сложении оба слагаемых имеют одинаковый знак, то операция сложения выполняется обычным путем. Если при сложении слагаемые имеют разные знаки, то сначала необходимо выявить большее по абсолютной величине число, произвести из него вычитание меньшего по абсолютной величине числа и разности присвоить знак большего числа. Выполнение операций умножения и деления в прямом коде выполняется обычным образом, но знак результата определяется по совпадению или несовпадению знаков участвовавших в операции чисел. Операцию вычитания в этом коде нельзя заменить операцией сложения с отрицательным числом, поэтому возникают сложности, связанные с заемом значений из старших разрядов уменьшаемого числа. В связи с этим прямой код в компьютере почти не применяется.

2. Обратный код числа N, обозначим [N]обр.

Пусть N= a1, a2, a3,... am и ā обозначает инверсию a, т.е. если a=1, то ā=0, и наоборот. Тогда:

При N>0, [N]обр =0, a1, a2, a3,... am;

При N<0, [N]обр =1, ā 1, ā 2, ā 3,... ā m;

При N=0 имеет место неоднозначность [0]обр.=0,00 …0 = 1,11…1

Для того чтобы получить обратный код отрицательного числа, необходимо все цифры этого числа инвертировать, то есть в знаковом разряде поставить 1, во всех значащих разрядах нули заменить единицами, а единицы нулями.

Например,

Для N=1011 [N]обр=0,1011;

Для N=-1011 [N]обр=1,0100.

3. Дополнительный код числа N,обозначим [N]доп.

Пусть так же N= a1, a2, a3,... am и ā обозначает инверсию a, т.е. если a=1, то ā=0, и наоборот. Тогда:

При N 0, [N]доп =0, a1, a2, a3,... am;

При N 0, [N]доп =1, ā 1, ā 2, ā 3,... ā m + 0,00 …1

Для того чтобы получить дополнительный код отрицательного числа, необходи­мо все его цифры инвертировать (в знаковом разряде поставить единицу, во всех значащих разрядах нули заменить единицами, а единицы нулями) и затем к млад­шему разряду прибавить единицу. В случае возникновения переноса из первого после запятой разряда в знаковый разряд, эта единица отбрасывается т.к. знаковый разряд только один.

Например,

Для N=1011 [N]доп=0,1011;

Для N=-1011 [N]доп=1,0101;

Для N=-0000, [N]доп=10,0000=0,0000 (1 исчезает)

 

Элементы двоичной арифметики

Рассмотрим, как выполняются арифметические действия в двоичной системе. Для этого проведем анализ таблиц сложения и умножения в двоичной системе:

0+0=0, 0*0=0, 0+1=1, 0*1=0, 1+1=10

Следует обратить внимание на аналогию в правилах выполне­ния арифметических действий в двоичной и десятичных системах счисления: если при сложении двух двоичных чисел (точнее, пред­ставленных в двоичной системе счисления) сумма цифр окажется больше единицы, то возникает перенос в старший разряд; если уменьшаемая цифра меньше вычитаемой, то нужно сделать «заем» единицы в старшем разряде.

Анализируя примеры умножения в двоичной системе счисле­ния, необходимо обратить внимание на одну важную особенность выполнения этой операции в данной системе. Так как очередная цифра множителя может быть только 1 или 0, то промежуточное произведение равно либо множимому, либо 0. Таким образом, опе­рация умножения в двоичной системе фактически не производится: в качестве промежуточного произведения записывается либо мно­жимое, либо 0, а затем промежуточные произведения суммируются. Иначе говоря, операция умножения заменяется последовательным сложением.

Как уже известно, дополнительный код используется для вычи­тания чисел в компьютерах и позволяет эту операцию свести к сло­жению чисел. Правила выполнения вычитания с дополнительным кодом сле­дующие: чтобы вычесть число А из числа В, достаточно сложить В с дополнительным кодом числа А и отбросить перенос в соседний стар­ший разряд.

Рассмотрим пример: 10110110₍₂₎ – 01000111₍₂₎

Найдем дополнительный код числа 01000111₍₂₎ он будет равен 10111001₍₂₎

10110110₍₂₎+ 10111001₍₂₎=01101111₍₂₎

1 0 1 1 0 1 1 0

+

1 0 1 1 1 0 0 1

_____________

1 0 1 1 0 1 1 1 1

 

Таким образом, важнейшее преимущество двоичной арифмети­ки заключается в том, что она позволяет все арифметические действия свести к одному – сложению, а это значительно упрощает устройство ЭВМ.

Практические задания

 

Задание 1. В восьмеричной системе счисления дано число. Перевести его в десятичную систему счисления.

№	Число	№	Число

 

 

Задание 2. Дано десятичное число. Перевести его в восьмеричную и в шестнадцатеричную системы счисления.

№	Число	№	Число

 

Задание 3. Перевести числа в двоичную систему счисления. Выполнить вычитание с использованием дополнительного кода.

№	Три числа в различных системах счисления.	№	Три числа в различных системах счисления.
	101111(2)+87(16)-53(10)=		85(10)+10001(2)-27(8)=
	1100100(2)-57(8)+3А(16)=		60(8)+10000111(2)-83(10)=
	46(8)+7В(16)-1000111(2)=		1100010(2)-66(8)+76(16)=
	10111100(2)-162(8)+28(10)=		57(8)+7С(16)- 1001101(2)=
	77(8)+73(16)-1001001(2)=		1011110(2)+5Е(16)-111(10)=
	125(10)+100101(2)-42(16)=		224(8)-110100(2)+23(16)=
	1101111(2)-39(10)+121(8)=		71(16)+101101(2)-85(10)=
	9Е(16)-1100101(2)+54(8)=		1110110(2)-4F(16)+164(8)=

 

Задание 4. Перевести оба действительных числа в двоичную систему счисления. Точность перевода чисел до 5 знаков после запятой. Записать числа в формате с плавающей запятой в нормализованной форме и выполнить сложение чисел.

 

№	Числа в десятичной системе счисления	№	Числа в десятичной системе счисления
	12,4 + 6,15 =		5,3 +7,15 =
	4,6 + 3,8 =		6,3 + 7,18 =
	7,3 +9,14 =		11,6 + 9,5 =
	14,5 +7,3 =		7,14 +2,6 =
	4,6 +7,8 =		5,13 + 13,5 =
	11,1 +4,6 =		8,4 +7,14 =
	13,11 +7,5 =		11,6 + 15,3 =
	3,6 +8,12 =		6,16 + 9,6 =

 

Контрольные вопросы

 

1. Что такое двоичные числа?

2. Какие системы счисления вы знаете?

3. Чем отличаются прямой, обратный и дополнительный коды числа?

4. Как производится вычитание двоичных чисел?

5. Как хранятся в компьютере числа с плавающей точкой?

 

Литература