Большое внимание в тестах уделяется вычислению производных. Вычисление производных осуществляется согласно правилам и формулам. Обратим внимание на функции вида:
у =  ,
,  .
.
у =  ,
,  .
.
у =  ,
,  .
.
Сравнивая данную функцию и ее производную, приходим к выводу: чтобы найти производную данной функции, нужно числитель умножить на показатель степени знаменателя с противоположным знаком, а показатель степени увеличить на единицу. Принятие во внимание этого факта поможет сэкономить время при вычислении производных такого вида на ЕНТ:
Тест1
1. Для функции у =  , определите:
, определите:
а) нули;
б) промежутки возрастания;
в) промежутки убывания.
Указание: 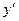 =
=  +
+ 
А) а) -4, 4; б) ( ); в) нет.
); в) нет.
В) а) -4, 4; б) ( ); в) нет.
); в) нет.
С) а) -4, 0; б) (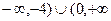 ); в) нет.
); в) нет.
D) а) -4, 4; б) ( ); в) [-4, 4].
); в) [-4, 4].
Е) а) -4, 0, 4; б)  );
);
в) ( ].
].
2. Дана функция f(x) =  . Найдите
. Найдите  .
.
А) 0. В) -3. С) 5. D) 1. Е) 6.
3. Для функции у = 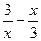 , определите:
, определите:
а) нули;
б) промежутки возрастания;
в) промежутки убывания.
А) а) -3, 3; б)нет; в) ( ).
).
В) а) -3, 3; б) ( ; в) [0,
; в) [0,  ).
).
С) а) -3, 3; б)нет; в) ( ).
).
D) а) -3, 0, 3; б)[-3, 0], [3,  ); в) (
); в) ( ).
).
Е) а) 3, -3; б) [3, 1], [-3, 0]; в) (0, -3], [0, 3].
4. Для функции у =  , найдите:
, найдите:
а) все критические точки;
б) точки минимума и точки максимума;
А) а)  ; б)
; б)  ,
,  ,
,  .
.
В) а)  ; б)
; б)  ,
,  .
.
С) а)  ; б)
; б) 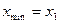 ,
, 
D) а)  ; б)
; б)  ,
,  .
.
Е) а)  ; б)
; б) 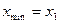 ,
, 
Производная сложной функции.
Очень часто при вычислении производных сложных функций учащиеся допускают ошибки. Находя производную функции y = lg(3x + 5), забывают умножить результат на 3. Почему? Просто многие из них не владеют понятием сложной функции. Поэтому при вычислении производных необходима последовательность рассуждений:
1. Определить вид функции (линейная, квадратичная, логарифмическая, степенная и т.д.)
2. Если – да, то ее производная берется согласно известным формулам.
3. Если – нет, то можно ли данную функцию представить в виде суммы (разности), произведения или частного указанных функций.
4. Если – да, то работаем с соответствующими формулами.
5. Если – нет, то надо рассматривать данную функцию как сложную.
Например:
Найти производную функции у = (2х – 4) 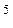 .
.
Последовательно рассуждая, приходим к выводу, что данная функция сложная: степенная от линейной. Значит, ее производная равна произведению производной степенной и линейной функций  10(2х – 4).
10(2х – 4).
Аналогичные примеры можно найти в следующих тестовых заданиях:
Тест 2.
1. Дана функция f(x) =  . Найдите
. Найдите  .
.
Решение: 
А) -42(4х + 7)  .
.
В) -6(4х + 7)  .
.
С) -4(4х + 7)  .
.
D) -24(4х + 7)  .
.
Е) -4(4х + 7)  .
.
2. Найдите производную функции у = (1/3 х – 6)  .
.
А) 8(1/3х – 6)  .
.
В) 6(1/3х – 6)  .
.
С) 24(1/3х – 6)  .
.
D) 1/3(1/3х – 6)  .
.
Е) 72(1/3х – 6)  .
.
3. Дано f(x) =  . Найдите
. Найдите  .
.
А) -10. В) 10. С) -60. D) 6. Е) 60.
4. Найдите производную функции: f(x) =  .
.
А)  . В)
. В)  . С)
. С)  . D)
. D)  . Е)
. Е) 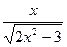 .
.
5. Найдите производную функции: f(x) = (2x – 6)  .
.
А) -7(2x – 6)  . В) 16(2x – 6)
. В) 16(2x – 6)  . С) -7(2x + 6)
. С) -7(2x + 6)  . D) 4(2x – 6)
. D) 4(2x – 6)  . Е) 8(2x – 6)
. Е) 8(2x – 6)  .
.
6. Дана функция  , найдите
, найдите 
А) 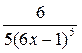 .
.
В) 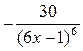 .
.
С) 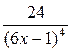 .
.
D)  .
.
Е) 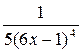 .
.
7. Найдите производную функции: f(x) =  .
.
А) 102x( .
.
В) 204  .
.
С) 102  .
.
D) 2x  .
.
Е) 204  .
.
8. Найдите производную функции: f(x) =  .
.
А) 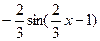 .
.
В)  .
.
С)  .
.
D) 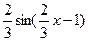 .
.
Е)  .
.
9. Найдите производную функции: y =  .
.
А)  .
.
В)  .
.
С)  .
.
D)  .
.
Е)  .
.






