Исследование функции целесообразно вести в определенной последовательности.
1. Найти область определения функции.
2. Выяснить, является ли функция четной, нечетной или общего вида.
3. Найти вертикальные асимптоты графика функции.
4. Исследовать поведение функции в бесконечности, найти горизонтальные и наклонные асимптоты.
5. Найти интервалы монотонности и экстремумы функции.
6. Найти интервалы выпуклости и точки перегиба.
7. Найти точки пересечения с осями координат.
8. Построить график функции.
Пример. Проведите исследование функции  и постройте ее график.
и постройте ее график.
По плану исследуем функцию 
1. Область определения D(f) – вся числовая ось, за исключением точек х = –2 и х = 2, т.е.
D(f) = (-¥; -2) È (-2; 2) È (2; +¥).
2. Функция непериодическая; исследуем ее на четность и нечетность: область определения симметрична относительно начала координат,
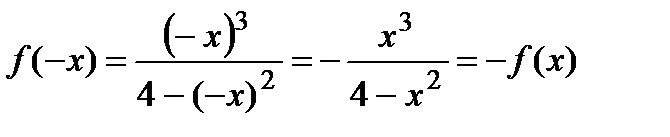 .
.
Следовательно, данная функция нечетная и ее график симметричен относительно начала координат. Поэтому далее исследуем функцию только при х ³ 0.
3. Определим вертикальные асимптоты функции:
 ,
,
т.е. прямая х = 2 – вертикальная асимптота. Отсюда в силу симметрии, следует, что прямая х = – 2 – также вертикальная асимптота.
4. Найдем наклонные асимптоты:

т.е. прямая у = – х – наклонная асимптота при х ® +¥ (то же и при х ® –¥).
5. Найдем интервалы монотонности и экстремумы функции, исследуя первую производную:
 .
.
Приравняв производную к нулю, определим критические точки: х =  и х = –
и х = –  .
.
– 
|
| –2 |

|
| + |
| + |
| + |
| – |
| – |
| f '(x) |
| f (x) |
| min |
| max |
Отсюда видно, что функция имеет минимум в точке х = – 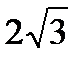 (причем f(–
(причем f(– 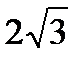 )»5,2) и максимум в точке х =
)»5,2) и максимум в точке х =  (причем f(
(причем f(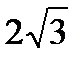 )» –5,2). Возрастает на интервалах (-
)» –5,2). Возрастает на интервалах (-  ; -2) È (-2; 2) È (2;
; -2) È (-2; 2) È (2; 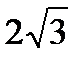 ) и убывает на интервалах (-¥; -
) и убывает на интервалах (-¥; -  ) È (
) È ( ; +¥).
; +¥).
6. Чтобы определить интервалы выпуклости и точки перегиба, вычислим вторую производную функции:
 .
.
Данное выражение обращается в нуль лишь при х = 0.
| f ¢¢(x) |
| х |
| – |
| + |
| –2 |
| – |
| + |
| перегиб |
Отсюда ясно, что на интервалах (-¥; -2) и (0; 2) функция выпукла вниз, а на интервалах (-2; 0) и (2; +¥) выпукла вверх, т.е. х = 0 – точка перегиба.
7. Найдем точки пересечения графика с осями координат: с осью Оу график пересекается при х = 0, откуда у = f(0) = 0, т.е. точка пересечения с осью Оу М(0;0) – единственная точка пересечения графика с осями.
Учитывая накопленную информацию, построим график функции.

Вариант 1
1. Вычислите производную 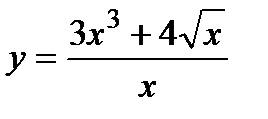 .
.
2. Вычислите производную 
3. Вычислите производную 
4. Найдите наибольшее и наименьшее значения функции 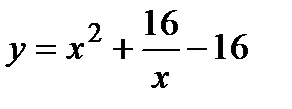 при
при 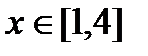 .
.
5. Исследуйте функцию 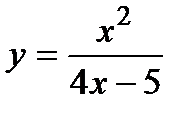 и постройте ее график.
и постройте ее график.
Вариант 2
1. Вычислите производную  .
.
2. Вычислите производную 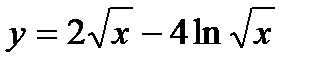 .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции  при
при 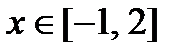 .
.
5. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Вариант 3
1. Вычислите производную  .
.
2. Вычислите производную  .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции  при
при 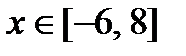 .
.
5. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Вариант 4
1. Вычислите производную  .
.
2. Вычислите производную 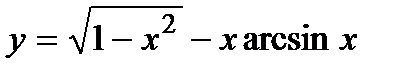 .
.
3. Вычислите производную 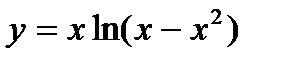 .
.
4. Найдите наибольшее и наименьшее значения функции  при
при 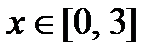 .
.
5. Исследуйте функцию 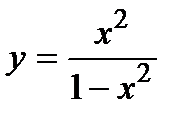 и постройте ее график.
и постройте ее график.
Вариант 5
1. Вычислите производную 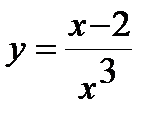 .
.
2. Вычислите производную  .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции 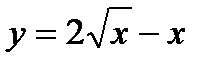 при
при 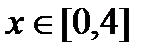 .
.
5. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Вариант 6
1. Вычислите производную  .
.
2. Вычислите производную  .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции  при
при  .
.
5. Исследуйте функцию 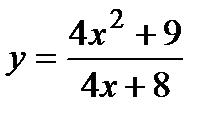 и постройте ее график.
и постройте ее график.
Вариант 7
1. Вычислите производную 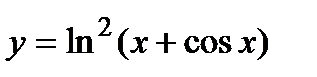 .
.
2. Вычислите производную 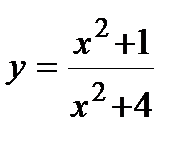 .
.
3. Вычислите производную 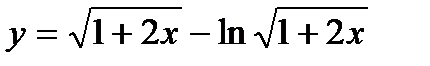 .
.
4. Найдите наибольшее и наименьшее значения функции 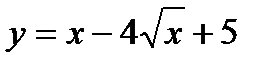 при
при 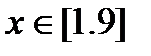 .
.
5. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Вариант 8
1. Вычислите производную 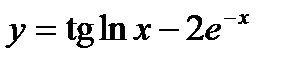 .
.
2. Вычислите производную  .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции  при
при 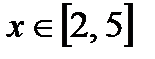
5. Исследуйте функцию 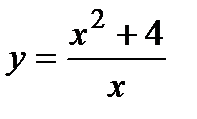 и постройте ее график.
и постройте ее график.
Вариант 9
1. Вычислите производную 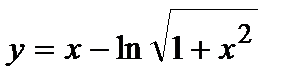 .
.
2. Вычислите производную 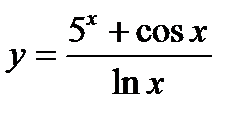 .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции  при
при  .
.
5. Исследуйте функцию 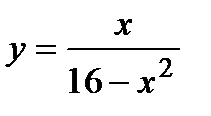 и постройте ее график.
и постройте ее график.
Вариант 10
1. Вычислите производную 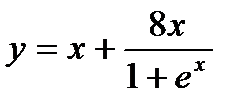 .
.
2. Вычислите производную 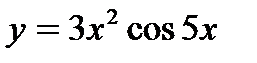 .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции 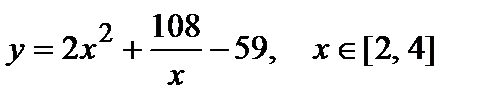 .
.
5. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Вариант 11
1. Вычислите производную 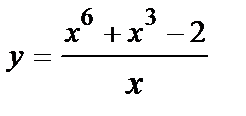 .
.
2. Вычислите производную 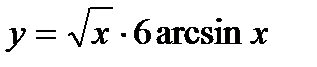 .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции  при
при 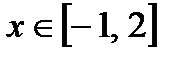 .
.
5. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Вариант 12
1. Вычислите производную  .
.
2. Вычислите производную 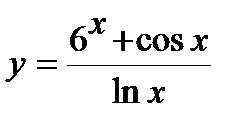 .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции  при
при  .
.
5. Исследуйте функцию 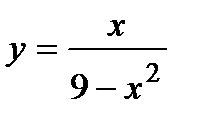 и постройте ее график.
и постройте ее график.
Вариант 13
1. Вычислите производную  .
.
2. Вычислите производную  .
.
3. Вычислите производную 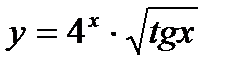 .
.
4. Найдите наибольшее и наименьшее значения функции  при
при  .
.
5. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Вариант 14
1. Вычислите производную 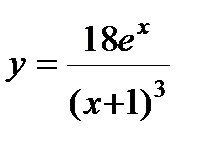 .
.
2. Вычислите производную 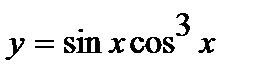 .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции 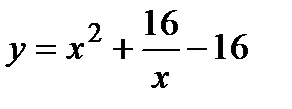 при
при 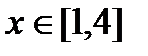 .
.
5. Исследуйте функцию 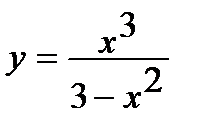 и постройте ее график.
и постройте ее график.
Вариант 15
1. Вычислите производную  .
.
2. Вычислите производную 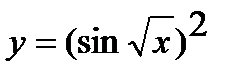 .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции  при
при  .
.
5. Исследуйте функцию 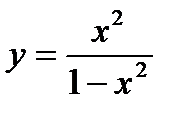 и постройте ее график.
и постройте ее график.
Вариант 16
1. Вычислите производную 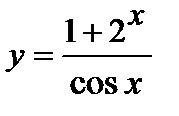 .
.
2. Вычислите производную  .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции 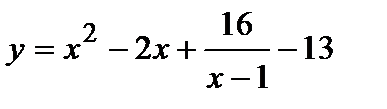 при
при  .
.
5. Исследуйте функцию 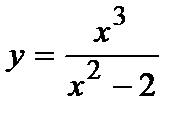 и постройте ее график.
и постройте ее график.
Вариант 17
1. Вычислите производную 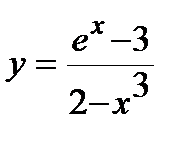 .
.
2. Вычислите производную 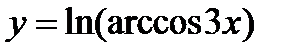 .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции  при
при  .
.
5. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Вариант 18
1. Вычислите производную  .
.
2. Вычислите производную  .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции  при
при  ..
..
5. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Вариант 19
1. Вычислите производную  .
.
2. Вычислите производную  .
.
3. Вычислите производную 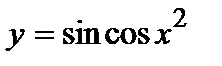 .
.
4. Найдите наибольшее и наименьшее значения функции 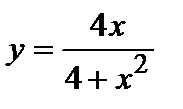 при
при 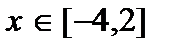 .
.
5. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Вариант 20
1. Вычислите производную 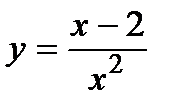 .
.
2. Вычислите производную 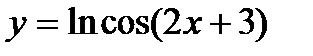 .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции  при
при  .
.
5. Исследуйте функцию 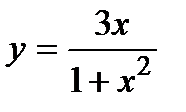 и постройте ее график.
и постройте ее график.
Вариант 21
1. Вычислите производную 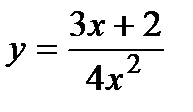
2. Вычислите производную 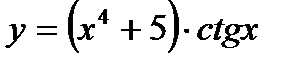 .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции 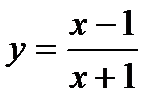 при
при  .
.
5. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Вариант 22
1. Вычислите производную  .
.
2. Вычислите производную  .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции  при
при  .
.
5. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Вариант 23
1. Вычислите производную 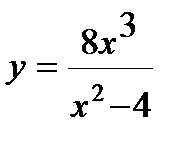 .
.
2. Вычислите производную  .
.
3. Вычислите производную 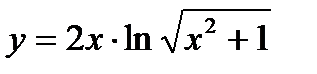 .
.
4. Найдите наибольшее и наименьшее значения 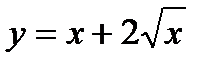 при
при 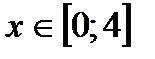 .
.
5. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Вариант 24
1. Вычислите производную  .
.
2. Вычислите производную 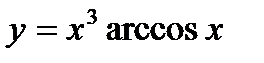 .
.
3. Вычислите производную 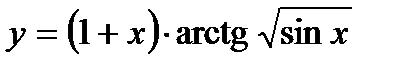 .
.
4. Найдите наибольшее и наименьшее значения функции 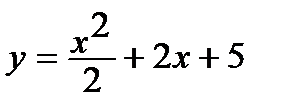 при
при  .
.
5. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Вариант 25
1. Вычислите производную 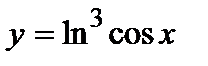 .
.
2. Вычислите производную  .
.
3. Вычислите производную  .
.
4. Найдите наибольшее и наименьшее значения функции 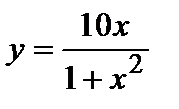 при
при  .
.
5. Исследуйте функцию  и постройте ее график.
и постройте ее график.






