Тема 2.3 Производная функции (повторение).
Основные понятия
Определение производной
Пусть в некоторой окрестности точки 
определена функция 
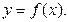Производной функции f в точке 
называется предел, если он существует,
Общепринятые обозначения производной функции
Правила дифференцирования
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу.
Если C — постоянное число и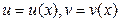 
— некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
Производная сложной функции
Сложная функция (композиция функций) записывается в виде
где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом (если функций больше, то промежуточным аргументом) для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция также дифференцируема по x и ее производная равна
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)! Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга.
Таблица производных функций независимой переменной.
| Функция | Производная | Функция | Производная | |
Постоянная
| 
| Тригонометрические
| 
| |
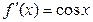
Степенная
| 
| |||
| 
| |||
| 
| |||
| 
| |||
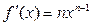
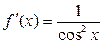
Логарифмическая
В частности
| 
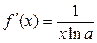
| Обратные тригонометрические
| 
| |
| ||||
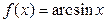
Показательная
В частности
| 
| |||
| 
| |||
| 
| 
| ||
| 
|
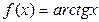
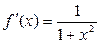
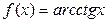
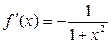
Таблица производных функций, аргументом которой является функция.
| Функция | Производная | Функция | Производная | |
| 
| 
| 
| |
| 
| |||
| 
| |||
| 
| 
| 
| |
| 
| |||
| 
| |||
| 
| 
| 
| |
| 
| |||
| 
| |||
| 
|
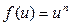
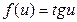
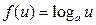
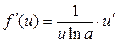
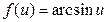
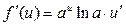
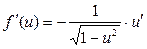
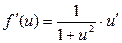
