Математик Ян Стюарт (Ian Stewart) в своей новой книге «В поисках неизвестного: 17 уравнений, которые изменили мир» рассматривает несколько наиболее важных уравнений всех времен.
Теорема Пифагора
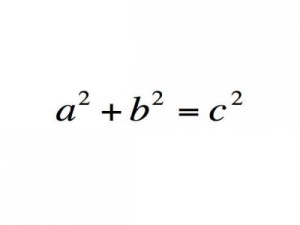
Теорема Пифагора
Согласно Теореме Пифагора в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Важность: Теорема Пифагора — важнейшее уравнение в геометрии, которое связывает ее с алгеброй и является основой тригонометрии. Без него было бы невозможно создать точную картографию и навигацию.
Современное использование: Триангуляция используется и по сей день, чтобы точно определить относительное расположение для GPS навигации.
Логарифм и его тождество

Логарифм и его тождество
Логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент.
Важность: Логарифмы стали настоящей революцией, позволив астрономам и инженерам делать расчеты более быстро и точно. С появлением компьютеров они не потеряли своего значения, поскольку все еще существенны для ученых.
Современное использование: Логарифмы важная составляющая для понимания радиоактивного распада.
Основная теорема анализа

Основная теорема анализа
Основная теорема анализа или формула Ньютона — Лейбница дает соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.
Важность: Теорема анализа фактически создала современный мир. Исчисление имеет важное значение в нашем понимание того, как измерять тела, кривые и площади. Она является основой многих природных законов и источником дифференциальных уравнений.
Современное использование: Любая математическая проблема, где требуется оптимальное решение. Существенное значение для медицины, экономики и информатики.
Классическая теория тяготения Ньютона

Классическая теория тяготения Ньютона
Классическая теория тяготения Ньютона описывает гравитационное взаимодействие.
Важность: Теория позволяет рассчитать силу гравитации между двумя объектами. Хотя позднее она была вытеснена теорией относительности Эйнштейна, теория все равно необходима для практического описания того, как объекты взаимодействуют друг с другом. Мы используем ее и по сей день для проектирования орбит спутников и космических аппаратов.
Современное использование: Позволяет найти наиболее энергоэффективные пути для вывода спутников и космических зондов. Также делает возможным спутниковое телевидение.
Комплексные числа

Комплексное число
Комплексные числа — расширение поля вещественных чисел.
Важность: Многие современные технологии, в том числе цифровые фотокамеры, не могли быть изобретены без комплексных чисел. Кроме того, они позволяют проводить анализ, который нужен инженерам для решения практических задач в авиации.
Современное использование: Широко используется в электротехнике и сложных математических теориях.
Эйлерова характеристика полиэдров

Эйлерова характеристика полиэдров
Важность: Внесла вклад в понимание топологического пространства, в котором рассматриваются только свойства непрерывности. Необходимый инструмент для инженеров и биологов.
Современное использование: Топология используется, чтобы понять поведение и функции ДНК.
Нормальное распределение

Нормальное распределение
Важность: Уравнение является основой современной статистики. Естественные и социальные науки не могли бы существовать в своей нынешней форме без него.
Современное использование: Используется для определения эффективности лекарств по сравнению с отрицательными побочными эффектами в клинических испытаниях.
Волновое уравнение

Волновое уравнение
Дифференциальное уравнение, описывающее поведение волн.
Важность: Волны исследуются с целью определения времени и места землетрясений, а также для прогнозирования поведения океана.
Современное использование: Нефтяные компании используют взрывчатку, а затем считывают данные от последующих звуковых волн для определения геологических формаций.
Преобразование Фурье

Преобразование Фурье
Важность: Уравнение позволяет разбивать, очищать и анализировать сложные шаблоны.
Современное использование: Используется при сжатии информации изображений в формате JPEG, а так же для обнаружения структуры молекул.
Уравнения Навье—Стокса

Уравнения Навье—Стокса
В левой части уравнения — ускорение небольшого количества жидкости, в правой — силы, которые воздействуют на него.
Важность: Как только компьютеры стали достаточно мощными, чтобы решить это уравнение, они открыли сложную и очень полезную области физики. Она особенно полезна для создания более качественной аэродинамики у транспортных средств.
Современное использование: Среди прочего, уравнение помогло в усовершенствовании современных пассажирских самолетов.
Уравнения Максвелла

Уравнения Максвелла
Описывают электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.
Важность: Помогли в понимании электромагнитных волн, что способствовало созданию многих технологий, которые мы используем сегодня.
Современное использование: Радар, телевидение и современные средства связи.
Второй закон термодинамики

Второй закон термодинамики
Вся энергия и тепло со временем исчезнет.
Важность: Имеет существенное значение для нашего понимания энергии и Вселенной через понятие энтропии. Открытие закона помогло улучшить паровой двигатель.
Современное использование: Помог доказать, что материя состоит из атомов, физики до сих пор пользуются этим знанием.
Теория относительности Эйнштейна

Теория относительности Эйнштейна
Энергия равна массе, умноженной на квадрат скорости света.
Важность: Наверное, самое известное уравнение в истории. Оно полностью изменило нашу точку зрения на материю и реальность.
Современное использование: Помогло создать ядерное оружие. Используется в GPS навигации.
Уравнение Шрёдингера

Нелинейное уравнение Шрёдингера
Описывает материю как волну, а не как частицу.
Важность: Перевернула представления физиков — частицы могут существовать в диапазоне возможных состояний.
Современное использование: Существенный вклад в использование полупроводников и транзисторов, и, таким образом, в большинство современных компьютерных технологий.
Информационная энтропия Шаннона
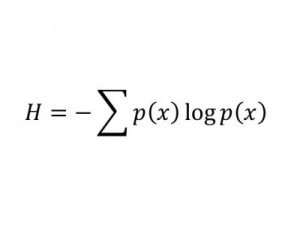
Информационная энтропия Шаннона
Оценивает количество данных в куске кода путем расчета вероятности его символов.
Важность: Это уравнение, которое открыло дверь в Информационную Эпоху.
Современное использование: В значительной степени все, что связано с обнаружением ошибок в кодировании (программировании).
Логистическая модель роста популяций

Логистическая модель роста популяций
Оценка изменений в популяции живых существ из поколения в поколение с ограниченными ресурсами.
Важность: Помогла в развитии теории хаоса, которая полностью изменила наше понимание того, как работают природные системы.
Современное использование: Используется для моделирования землетрясений и прогноза погоды.
Модель Блэка-Скоулза

Модель Блэка Скоулза
Одна из моделей ценообразования опционов.
Важность: Помогла создать несколько триллионов долларов. Согласно некоторым экспертам, неправильное использование формулы (и ее производных) способствовало финансовому кризису. В частности, уравнение имеет несколько предположений, которые не справедливы на реальных финансовых рынках.
Современное использование: Даже после кризиса используются для определения цен.
Вместо заключения
В мире существует множество других важных уравнений и формул, которые изменили судьбу человечества в целом и нашу личную жизнь в частности. Среди них, модель Ходжкина—Хаксли, Фильтр Калмана и, конечно, уравнение поисковой системы Google. Мы надеемся, что нам удалось показать насколько важна математика, и насколько бесценен ее вклад для всех людей.






