1. Обчислити інтеграл від раціональної функції: 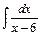
Розв'язання. Використаємо формулу (6)
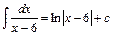 .
.
2. Обчислити інтеграл від раціональної функції: 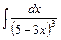
Розв'язання. Для цього інтеграла здійснимо заміну змінної 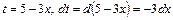
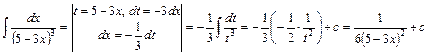 ;
;
3. Обчислити інтеграл від раціональної функції: 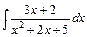
Розв'язання. Для знаходження цього інтеграла можна застосувати формулу (8), оскільки виконується умова 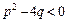 . Однак обчислимо цей інтеграл виділенням у знаменнику повного квадрату:
. Однак обчислимо цей інтеграл виділенням у знаменнику повного квадрату:
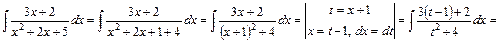
= 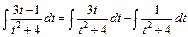 .
.
Перший інтеграл проінтегруємо методом заміни z=t2 +4, dz=2tdt
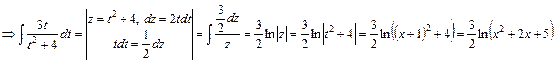
Другий інтеграл табличний і за формулою (9) дістанемо
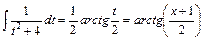 .
.
Отже, 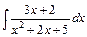
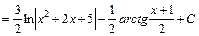 .
.
4. Обчислити інтеграл від раціональної функції: 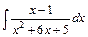 .
.
Розв'язання. Для обчислення цього інтеграла не можна застосувати формулу (8), оскільки p2- 4 q =36-20=16>0. Обчислимо його двома способами.
а. Квадратний тричлен у знаменнику має корені, тому розкладається на множники:
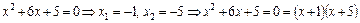 .
.
Розкладемо раціональний дріб на суму найпростіших дробів, застосувавши метод невизначених коефіцієнтів:
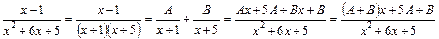 .
.
Прирівнявши коефіцієнти многочленів чисельника при відповідних степенях змінної 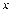 дістанемо систему рівнянь відносно коефіцієнтів
дістанемо систему рівнянь відносно коефіцієнтів 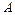 і
і 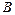 :
:
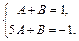
Розв’язком цієї системи є 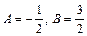 . Тому
. Тому 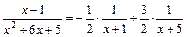 . Отже,
. Отже,
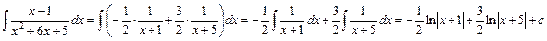 .
.
б. Виділимо повний квадрат у знаменнику та здійснимо заміну:
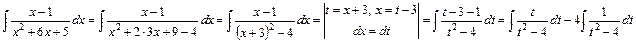 .
.
Інтеграл 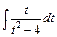 знайдемо, здійснивши заміну
знайдемо, здійснивши заміну 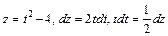 :
:
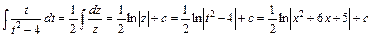 .
.
Інтеграл 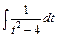 табличний, та згідно формули (13) таблиці інтегралів
табличний, та згідно формули (13) таблиці інтегралів 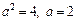 дістанемо
дістанемо
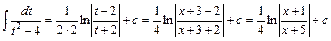 .
.
Отже, 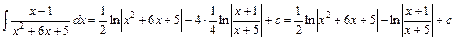 .
.
Отримані результати першим та другим способами по формі є різними, а по значенню – тотожними. Дійсно,
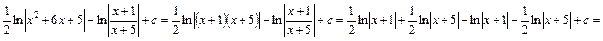
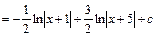 .
.
Другий спосіб є більш зручним у разі, коли квадратний тричлен має ірраціональні корені. У цьому випадку розклад раціонального дробу на найпростіші дроби стає громіздким, оскільки коефіцієнтами при невідомих у системі рівнянь є ірраціональні числа. Наприклад, для інтегралу
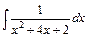
квадратний тричлен знаменника 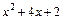 має корені
має корені 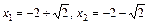 . Тому
. Тому
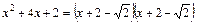 , та
, та 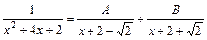 .
.
Подальші перетворення стають громіздкими. В той час, як другим способом маємо:
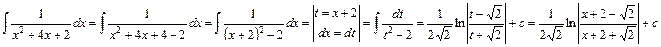
5. Обчислити інтеграл від раціональної функції: 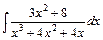 .
.
Розв'язання. Розкладемо підінтегральний раціональний дріб на елементарні раціональні дроби:
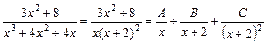 ,
,
де A, B, C невідомі коефіцієнти розкладу. Щоб їх знайти зведемо праву частину до спільного знаменника і, прирівнявши чисельники, матимемо:
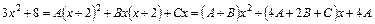 .
.
Прирівнявши коефіцієнти при однакових степенях х одержимо систему рівнянь
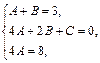
розв'язком якої є 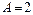 ,
, 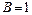 ,
, 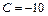 , тобто
, тобто 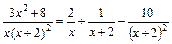 . Отже
. Отже
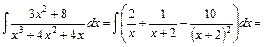
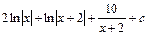 .
.
6. Обчислити інтеграл від раціональної функції: 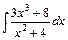 .
.
Розв'язання. Підінтегральна функція є неправильним раціональним дробом. Виділимо цілу частину цього дробу і правильний раціональний дріб:
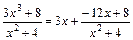 .
.
Тому 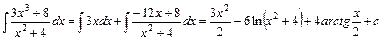 .
.
Завдання для самостійного розв'язання
5. Проінтегрувати раціональні дроби
1) 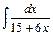 , 2)
, 2) 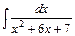 , 3)
, 3) 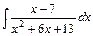 ,4)
,4) 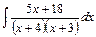 ,
,
5) 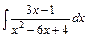 , 6)
, 6) 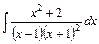 , 7)
, 7) 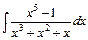 .
.






