Функцію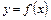 
називають раціональною, якщо її можна подати у вигляді 
, де 
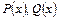– многочлени з дійсними коефіцієнтами.
Якщо степінь многочлена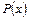 
менший за степінь многочлена 
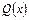, то раціональну функцію називають правильною, я якщо більший або дорівнює йому, – то неправильною. Неправильну раціональну функцію завжди можна перетворити на правильну, виділивши цілу частину
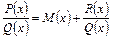, (4)
де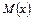 
, 
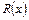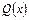, деякі многочлени, та степінь многочлена 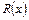менший за степінь многочлена .
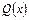Надалі будемо розглядати саме правильні раціональні функції.
Якщо 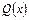– многочлен степеня 
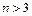, то його завжди можна розкласти на такі множники:
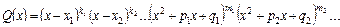, (5)
де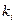 
– кратність коренів 
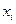, а квадратні вирази 
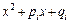не мають дійсних коренів, тобто, не розкладаються на множники. Тоді правильний раціональний дріб 
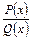єдиним чином представляється у вигляді суми найпростіших раціональних дробів:
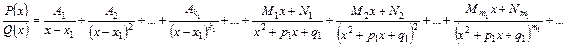
Якщ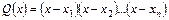о 
, то
.
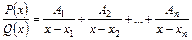Розклад правильної раціональної функції на найпростіші раціональні дроби здійснюється методом невизначених коефіцієнтів. Якщо множники в знаменнику є двочлени у першому степені, то такий дріб розкладається на суму дробів, у яких знаменниками є двочлен, а в чисельнику стала величина Наприклад:
.
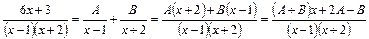Оскільки перший і останній дроби рівності однакові та однакові їхні знаменники, то повинні бути однаковими також їхні чисельники:
.
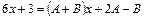Із цієї рівності відносно A та B дістанемо систему рівнянь:
.
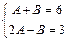Розв’язком цієї системи є A= 3, B =3. Отже,
.
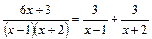Якщо в знаменнику двочлен має степінь 2, то при розкладі на найпростіші дроби будуть міститись два дроби, у яких знаменником для першого дробу буде двочлен в першому степені, а для другого – цей самий двочлен в другому степені. Чисельниками будуть сталі величини.
.
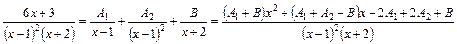Так як перший і останній дроби рівності однакові, їхні знаменники однакові, то повинні бути однаковими й чисельники. Два многочлена однакові, якщо однакові відповідні коефіцієнти при однакових степенях змінної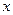 
. Це призводить до системи лінійних рівнянь відносно невизначених коефіцієнтів 
:
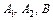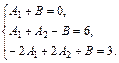
Розв'язком цієї системи є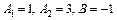 
. Отже 
.
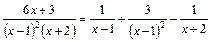Якщо ж у знаменнику буде множником квадратний тричлен, який не розкладається на множники, то при розкладі на найпростіші дроби, знаменником якого буде цей тричлен, у чисельнику буде знаходитись двочлен виду Ax+B.
.
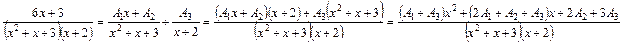Прирівнявши чисельники першого та останнього дробів цієї рівності, дістанемо систему рівнянь відносно невідомих коефіцієнтів:
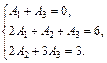
Розв’язком цієї системи є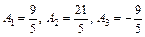 
. Отже,
.
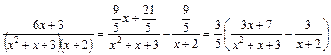Таким чином, інтегрування правильного раціонального дробу зводиться до інтегрування таких найпростіших раціональних дробів:
1. 
.
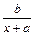2. 
, 
.
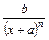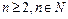3. 
, 
.
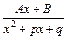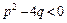4. 
, 
, .
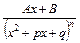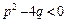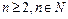Для інтегрування раціонального дробу використовують алгоритм:
1 крок (виконується для неправильних дробів). Виділити цілу частину 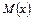та правильний дріб 
.
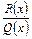2 крок Розкласти многочлен 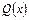на множники (5)
3 крок. Розкласти дріб 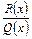на суму найпростіших раціональних дробів методом невизначених коефіцієнтів.
4 крок. Проінтегрувати цілу частину 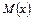і кожний з утворених найпростіших раціональних дробів. Останній крок алгоритму можливий завдяки використання наступних формул:
