Пример 1. Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции 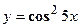
Решение:
- Придаем аргументу
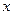 произвольное приращение
произвольное приращение  и, подставляя в данное выражение функции вместо
и, подставляя в данное выражение функции вместо 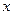 наращенное значение
наращенное значение  , находим наращенное значение функции
, находим наращенное значение функции 
В данном случае 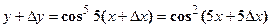
- Находим приращение функции
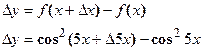
- Делим приращение функции на приращение аргумента, т. е. составим отношение

- Ищем предел этого отношения при
 . Этот предел и даст искомую производную
. Этот предел и даст искомую производную 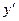 от функции
от функции  ;
; 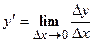
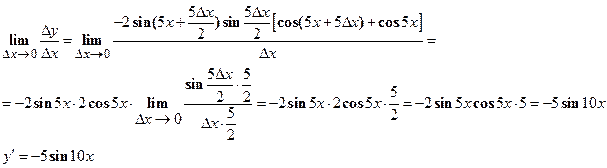
| Таблица производных | |
| Производные простых функций | Производные обратных тригонометрических функций |
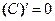
| 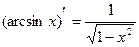
|
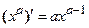
| 
|
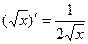
| 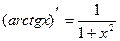
|
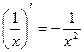
| 
|

| |
| Производные экспоненциальных и логарифмических функций | Производные гиперболических функций |
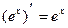
| 
|

| 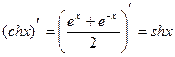
|
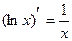
| 
|
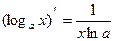
| 
|
| Производные тригонометрических функций | |
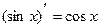
| 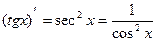
|
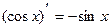
| 
|
| Правила дифференцирования | |
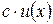
| 
|
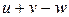
| 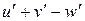
|

| 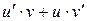
|
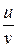
| 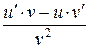
|
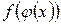
| 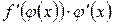
|
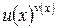
| 
|






