Теорема 1. Если функция 
дифференцируема в точке 
, то она непрерывна в этой точке.
Теорема 2. Пусть функция имеет производную в данной точке x. Тогда функция 
, где C - постоянная, также имеет в этой точке производную, причем 
.
Теорема 3. Пусть функции 
и 
имеют производные в данной точке x. Тогда сумма и разность этих функций также имеют в этой точке производные, причем 
.
Теорема 4. Пусть функции и имеют производные в данной точке x. Тогда произведение этих функций также имеет в этой точке производную, причем 
.
Теорема 5. Пусть функции и имеют производные в данной точке x. Тогда частное этих функций при условии, что 
также имеет в этой точке производную, причем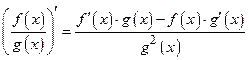 
.
Производной сложной функции
Теорема. Пусть функция 
дифференцируема в некоторой точке , а функция 
дифференцируема в точке 
. Тогда сложная функция 
дифференцируема в указанной точке и справедлива следующая формула 
