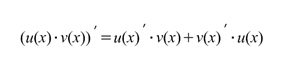Таблица первообразных ("интегралов"). Таблица интегралов. Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром). Формулы интегрирования по частям. Формула Ньютона-Лейбница.
| Таблица первообразных ("интегралов"). Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром). | |
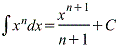 Интеграл степенной функции.
Интеграл степенной функции.
|  Интеграл степенной функции.
Интеграл степенной функции.
|
 Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала.
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала.
| |
 Интеграл экспоненциальной функции.
Интеграл экспоненциальной функции.
|  Интеграл экспоненты, где a-постоянное число.
Интеграл экспоненты, где a-постоянное число.
|
 Интеграл сложной экспоненциальной функции.
Интеграл сложной экспоненциальной функции.
| 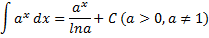 Интеграл экспоненциальной функции.
Интеграл экспоненциальной функции.
|
 Интеграл, равняющийся натуральному логорифму.
Интеграл, равняющийся натуральному логорифму.
|  Интеграл: "Длинный логарифм".
Интеграл: "Длинный логарифм".
|

| 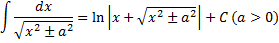 Интеграл: "Длинный логарифм".
Интеграл: "Длинный логарифм".
|
 Интеграл: "Высокий логарифм".
Интеграл: "Высокий логарифм".
| 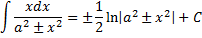 Интеграл, где х в числителе заводится под знак дифференциала (константу под знаком можно как прибавлять, так и отнимать), в итоге схож с интегралом, равным натуральному логорифму.
Интеграл, где х в числителе заводится под знак дифференциала (константу под знаком можно как прибавлять, так и отнимать), в итоге схож с интегралом, равным натуральному логорифму.
|
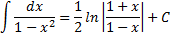 Интеграл: "Высокий логарифм".
Интеграл: "Высокий логарифм".
| |
 Интеграл косинуса.
Интеграл косинуса.
|  Интеграл синуса.
Интеграл синуса.
|
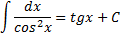 Интеграл, равный тангенсу.
Интеграл, равный тангенсу.
| 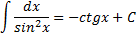 Интеграл, равный котангенсу.
Интеграл, равный котангенсу.
|
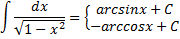 Интеграл, равный как арксинусу, так и арккосинусу
Интеграл, равный как арксинусу, так и арккосинусу
|  Интеграл, равный как арктангенсу, так и арккотангенсу.
Интеграл, равный как арктангенсу, так и арккотангенсу.
|
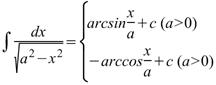 Интеграл, равный как арксинусу, так и арккосинусу.
Интеграл, равный как арксинусу, так и арккосинусу.
|  Интеграл, равный как арктангенсу, так и арккотангенсу.
Интеграл, равный как арктангенсу, так и арккотангенсу.
|

| |
 Интеграл равный косекансу.
Интеграл равный косекансу.
|  Интеграл, равный секансу.
Интеграл, равный секансу.
|
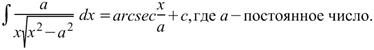 Интеграл, равный арксекансу.
Интеграл, равный арксекансу.
|  Интеграл, равный арккосекансу.
Интеграл, равный арккосекансу.
|
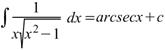 Интеграл, равный арксекансу.
Интеграл, равный арксекансу.
| 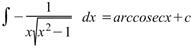 Интеграл, равный арксекансу.
Интеграл, равный арксекансу.
|
 Интеграл, равный гиперболическому синусу.
Интеграл, равный гиперболическому синусу.
|  Интеграл, равный гиперболическому косинусу.
Интеграл, равный гиперболическому косинусу.
|
 Интеграл, равный гиперболическому тангенсу.
Интеграл, равный гиперболическому тангенсу.
|  Интеграл, равный гиперболическому котангенсу.
Интеграл, равный гиперболическому котангенсу.
|
 Интеграл, равный гиперболическому синусу, где sinhx - гиперболический синус в ангийской версии.
Интеграл, равный гиперболическому синусу, где sinhx - гиперболический синус в ангийской версии.
|  Интеграл, равный гиперболическому косинусу, где sinhx - гиперболический синус в ангийской версии.
Интеграл, равный гиперболическому косинусу, где sinhx - гиперболический синус в ангийской версии.
|
 Интеграл, равный гиперболическому тангенсу.
Интеграл, равный гиперболическому тангенсу.
|  Интеграл, равный гиперболическому котангенсу.
Интеграл, равный гиперболическому котангенсу.
|
 Интеграл, равный гиперболическому секансу.
Интеграл, равный гиперболическому секансу.
|  Интеграл, равный гиперболическому косекансу.
Интеграл, равный гиперболическому косекансу.
|
Формулы интегрирования по частям. Правила интегрирования.
| Формулы интегрирования по частям. Формула Ньютона-Лейбница.Правила интегрирования. | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Интегрирование произведения (функции) на постоянную: | 
| |||||||||||||||||||||||||||||||||||||||||||||||||
| Интегрирование суммы функций: | 
| |||||||||||||||||||||||||||||||||||||||||||||||||
| Формула интегрирования по частям неопределенные интегралы: | 
| |||||||||||||||||||||||||||||||||||||||||||||||||
| Формула интегрирования по частям определенные интегралы: | 
| |||||||||||||||||||||||||||||||||||||||||||||||||
| Формула Ньютона-Лейбница определенные интегралы: |  Где F(a),F(b)-значения первообразных в точках b и a соответственно.
Где F(a),F(b)-значения первообразных в точках b и a соответственно.
| |||||||||||||||||||||||||||||||||||||||||||||||||
Таблица производных. Табличные производные. Производная произведения. Производная частного. Производная сложной функции.
Если x - независимая переменная, то:
| ||||||||||||||||||||||||||||||||||||||||||||||||||





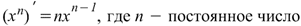 Производная степенной функции
Производная степенной функции
 Производная степенной функции
Производная степенной функции
 Производная экспоненциальной функции
Производная экспоненциальной функции
 Производная экспоненты
Производная экспоненты
 Производная сложной экспоненциальной функции
Производная сложной экспоненциальной функции
 Производная экспоненциальной функции
Производная экспоненциальной функции
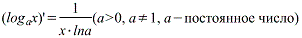 Производная логарифмической функции
Производная логарифмической функции
 Производная натурального логарифма
Производная натурального логарифма
 Производная натурального логарифма функции
Производная натурального логарифма функции
 Производная синуса
Производная синуса
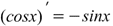 Производная косинуса
Производная косинуса
 Производная косеканса
Производная косеканса
 Производная секанса
Производная секанса
 Производная арксинуса
Производная арксинуса
 Производная арккосинуса
Производная арккосинуса
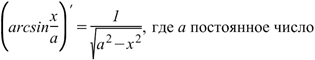 Производная арксинуса
Производная арксинуса
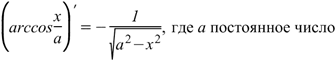 Производная арккосинуса
Производная арккосинуса
 Производная тангенса
Производная тангенса
 Производная котангенса
Производная котангенса
 Производная арктангенса
Производная арктангенса
 Производная арккотангенса
Производная арккотангенса
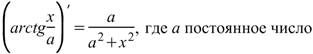 Производная арктангенса
Производная арктангенса
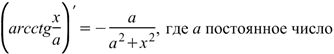 Производная арккотангенса
Производная арккотангенса
 Производная арксеканса
Производная арксеканса
 Производная арккосеканса
Производная арккосеканса
 Производная арксеканса
Производная арксеканса
 Производная арккосеканса
Производная арккосеканса
 Производная гиперболического синуса
Производная гиперболического синуса
 Производная гиперболического синуса в английской версии
Производная гиперболического синуса в английской версии
 Производная гиперболического косинуса
Производная гиперболического косинуса
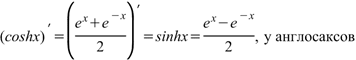 Производная гиперболического косинуса в английской версии
Производная гиперболического косинуса в английской версии
 Производная гиперболического тангенса
Производная гиперболического тангенса
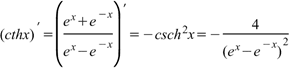 Производная гиперболического котангенса
Производная гиперболического котангенса
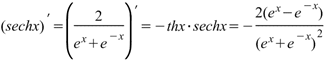 Производная гиперболического секанса
Производная гиперболического секанса
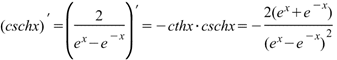 Производная гиперболического косеканса
Производная гиперболического косеканса