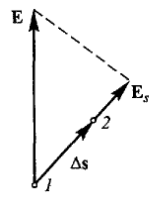
Рассмотрим заряд q в однородном поле Е. Пусть он переходит из точки 1 в точку 2 вдоль отрезка ∆S.
При этом производится работа
∆А=ES·∆S, (1)
которая в свою очередь равна U12. Приращение потенциала U=U21 =-U12=-∆φ. Отсюда имеем
ES= ∆φ/∆S, (2)
или
ES= dφ/dS. (3)
Т.е. проекция напряженности поля на данное направление равна быстроте изменения потенциала в данном направлении.
Как не трудно увидеть из рисунка, быстрейшим образом потенциал меняется в направлении Е. Направление наибольшего изменения любой скалярной функции φ определяется вектором, который называют градиентом grad φ. Величина градиента равна производной функции по направлению ее быстрейшего увеличения.
Таким образом
= -grad φ. (4)
Т.е. напряженность электрического поля равна градиенту потенциала с обратным знаком. Знак минус указывает на то, что напряженность направлена в сторону уменьшения потенциала.
Геометрическое место точек, в которых потенциал имеет одно и то же значение называется эквипотенциальной поверхностью. Вектор напряженности поля всегда направлен по нормали к эквипотенциальной поверхности в данной точке.
Найдем потенциал поля точечного заряда.
Учитывая, что потенциал не зависит от формы пути, предположим, что заряд движется вдоль r в бесконечность. Тогда, интегрируя Е по r, находим
φ = 
= q/4πe0· 
= 1/4πe0·q/r. (5)
Видно, что потенциал убывает пропорционально расстоянию. Эквипотенциальными поверхностями являются сферы.
Если поле создается системой зарядов, то в силу принципа суперпозиции
φ = 
. (6)
