Если функция 
дифференцируема в точке 
, а функция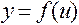 
дифференцируема в точке 
, то сложная функция 
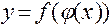дифференцируема в точке и
,
где индекс внизу показывает, по какой переменной берется производная.
Задача 4. Найти производные следующих функций:
а) 
; г) 
;
б) 
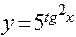; д) 
.
в) 
;
Решение. а) Функцию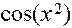 
представим как композицию функций 
и 
. Используя таблицу производных, находим: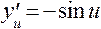 
, 
.
Тогда
.
б) Функцию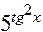 
представим как композицию функций 
,
и 
.Найдем производные по промежуточным аргументам: 
, 
и 
.
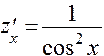Производную сложной функции находим по формуле 
. Окончательно получим 
= 
.
Аналогично решается задача в:
=
= 
= 
.
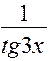
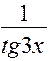
г) Предварительно упростив выражение, определяющее функцию, до вида
,
находим производную:
.
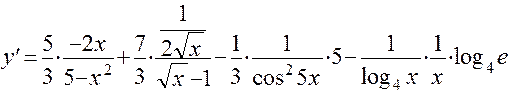д) Прологарифмируем обе части равенства, задающего функцию
.
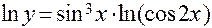Находя производные от левой и правой частей этого тождества, получим
Вычисляя производную от правой части тождества и решая уравнение относительно 
, получим
.
Производные высших порядков
Производная от функции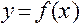 
также определяется функцией от 
и может быть дифференцируема.
Производная от производной функции 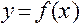называется производной второго порядка от функции 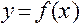и обозначается:
.
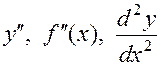Аналогично определяются производные третьего, четвертого и более высоких порядков.
Задача 5. Найти 
и 
для функции 
;
Решение. Найдем сначала 
:
= 
= 
.
Затем находим вторую производную:
=
.
