Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ
Методические указания
К выполнению индивидуальных заданий
по теме:
«Приложения производной»
Волгодонск
Правило Лопиталя
Теорема Лопиталя. Пусть функции 
и 
дифференцируемы в некоторой окрестности точки 
за исключением, может быть, самой точки и непрерывны в этой окрестности (включая саму точку ), причем 
и 
= 
=0. Тогда, если существует 
, то существует 
и эти пределы равны, то есть 
Таким образом, для нахождения предела (для раскрытия неопределенностей типа (
)) достаточно найти производные числителя и знаменателя дроби и вычислить предел . Такое же правило применяется при 
, а также для раскрытия неопределенностей типа (
).
Замечание. Если производные числителя и знаменателя в свою очередь стремятся к нулю или 
, то описанное правило применяется повторно и так далее.
Для вычисления предела вида 
,
где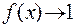 
и 
, или 
и 
,
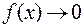или 
и , можно использовать описанное правило, предварительно прологарифмировав выражение 
.
Задача 1. Вычислить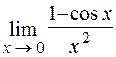 
.
Решение: 
.
Задача 2. Вычислить 
.
Решение:
.
Задача 3. Вычислить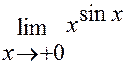 
.
Решение:
Ясно, что рассматриваемый предел представляет собой неопределенность типа 
. Логарифмируем выражение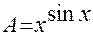 
, получаем 
.
С учетом последнего равенства находим
= 
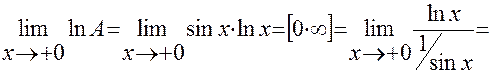
0.
Воспользовавшись непрерывностью функции 
на вcей естественной области определения, получим: 
. Отсюда 
=1.
Следовательно, 
=1.
